Задачи нелинейного программирования если сравнивать с задачами линейного программирования владеют громадным многообразием. На рис. 17-3 представлены вероятные варианты размещения точки экстремума для случая двух переменных. Так, при линейных нелинейной функции и ограничений цели экстремума возможно достигнуть в крайней точке (вершине) допустимой области значений (рис. 17-3, а), в одной из точек, лежащих на ограничивающих прямых (рис. 17-3, б), и, наконец, в точке, расположенной в области (рис. 17-3, в). Пунктирные концентрические окружности изображают линии постоянных значений функции цели, целые линии — границу области допустимых значений. При на рис. 17-3, б — экстремум определяется как точка касания прямой, ограничивающей допустимую область значений, и линии равных значений функции цели.
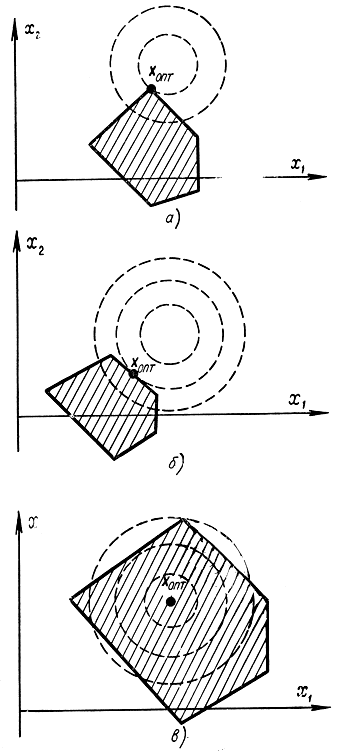
Рис. 17-3. Разные случаи оптимума в задачах нелинейного программирования
Рис. 17-4. Случай двух экстремумов при односвязной области допустимых значений
Ответ задач нелинейного программирования может давать два либо более экстремума, в то время как ответ задач линейного программирования дает один экстремум. На рис. 17-4 продемонстрирован случай, соответствующий линейным ограничениям и нелинейной (квадратичной) функции цели, где она достигает большого значения в двух точках А (локальный максимум) и В (глобальный максимум). На этом рисунке пунктиром обозначены постоянные значения функции цели F = const = Сi, целой линией ограничена область допустимых значений. При нелинейных ограничениях может иметь место случай многосвязной области допустимых значений, и в каждой изолированной подобласти функция цели может быть около собственного одного либо нескольких локальных экстремумов. На рис. 17-5 представлен случай двусвязной области, в которой функция цели достигает локальных экстремумов. Максимум в точке В — глобальный для всей области допустимых значение, в точке А – локальный.
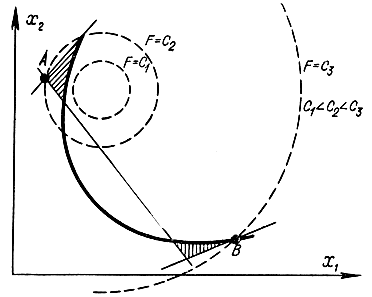
Рис. 17-5. Случай двух экстремумов при двусвязной области допустимых значений
17-3. Хорошие способы определения экстремума функции
а) Задача на полный экстремум
В случае, если постоянная функция n переменных x = (x1,…,xn) F(х) имеет в точке хопт максимум, то существует ? 0 такое, что для всех x из ?-окрестности точки хопт
F(x)?F(xопт)
либо
F(x)-F(xопт)?0.
Выберем два вида приращения xj на протяжении j-й координаты
?xj=xj-xjопт0,
?xj=xj-xjопт
Тогда
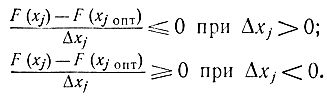
Переходя в этих соотношениях к пределу при ?xj0, приобретаем:
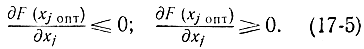
Из этих соотношений направляться, что
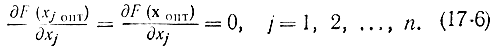
Подобное соотношение возможно взять для случая минимума функции. Так, доказана необходимость условий (17-6) с целью достижения в точке хопт максимума либо минимума функции F(х), т. е. в случае, если имеется экстремум, то условия (17-6) удовлетворяются. Но равенство нулю всех производных в точке хопт еще не снабжает существования в ней экстремума, т. е. условия (17-6) не являются достаточными. Геометрически это указывает, что при нулевой производной от функции одной переменной может иметь место точка перегиба, а не максимум (либо минимум), а при функции двух переменных — седловая точка, а не экстремум и т. д. Исходя из этого точки хопт, в которых выполняются соотношения (17-6), именуются стационарными.
Увидим, что условие (17-6) удалось взять благодаря возможности придавать переменной х приращения двух знаков, откуда и появились два неравенства (17-5). В случае, если допустимая область значений х ограничена неотрицательными значениями х?0, то в области, где х 0, справедливость условия (17-6) сохраняется, поскольку в том месте допустимы приращения обоих знаков. На границе области х ? 0, где х = 0, допускается лишь хорошее приращение ?х 0, возможно сказать лишь об односторонней производной, и из (17-6) направляться следующее нужное условие максимума:
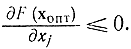
Нужное условие минимума на границе области хj = 0 запишется в виде
.
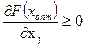б) Задача на условный экстремум
При определении условного экстремума функции, в то время, когда требуется выяснить максимум (либо минимум) функции F(х) при ограничивающих условиях:
?i(x) = bi, i = 1, …, m,
т. е.
F(x)=max;
?i(x)=bi;
употребляется кроме этого способ множителей Лагранжа, что, так же как при хорошего вариационного исчисления (гл. 11), содержится во введении функции Лагранжа
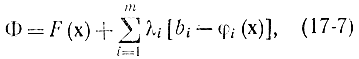
где ?i — неизвестные множители Лагранжа.
Полагая, что функция есть частным случаем функционала, либо используя способы, подобные использованным в гл. 11 (§ 6), приобретаем, что нужные условия экстремума находятся прямым дифференцированием соотношения (17-7) и записываются в виде
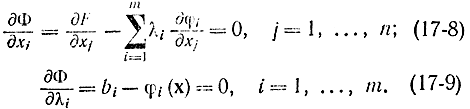
В случае, если ввести в рассмотрение векторы
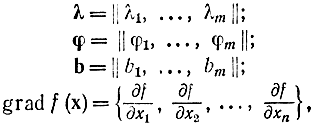
соотношения (17-8) и (17-9) перепишутся как
grad ? = grad F — ? grad ? = 0;
b — ? = 0,
где равенство нулю векторов понимается покомпонентно.
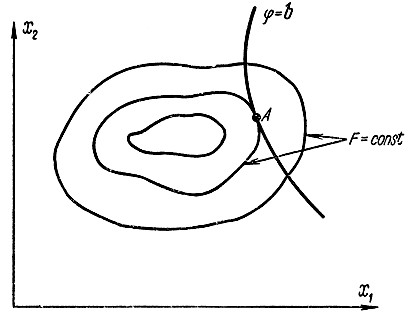
Рис. 17-6. Пояснение к задаче на условный экстремум
При n = 2 и m = 1 геометрическая задача об отыскании условного экстремума сводится (рис. 17-6) к отысканию точки касания А кривой ? = b к одной из кривых постоянного уровня F = const.
в) Минимаксная трактовка задачи на условный экстремум функции
Предположим, что функция F (х) имеет в точке хопт максимум при ограничивающих условиях ?i (х) = bi (i = 1,…, m). Соответствующий данной точке множитель Лагранжа обозначим через ?опт = ||?1опт,…,?mопт ||. В случае, если исключить особенные случаи, то можно считать, что функция Лагранжа ? (х, ?опт) имеет в точке хопт абсолютный максимум, т. е.
? (x, ?опт) ? ? (xопт, ?опт)
для всех х из некоей малой ?-окрестности точки хопт. Снова, кроме из рассмотрения особенные случаи, думаем, что для некоей окрестности ? точки ?опт функция ? (x, ?) имеет абсолютный максимум по х и удовлетворяет условиям
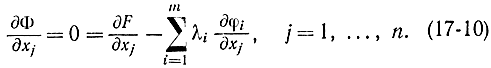
Будем вычислять, что эти уравнения имеют единственное ответ х при любом ? из ?-окрестности ?опт. Тогда точку максимума хопт возможно разглядывать как функцию и от и для ?-окрестности ?опт возможно записать:
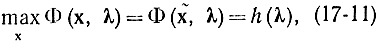
т. е. максимум по х будет функцией от ?. Разумеется, что
h(?опт) = ? (xопт, ?опт) = F (xопт)
так как при ? = ?опт и х = хопт, и ?i (х) = bi, и
?(х, ?) = F (х).
Обозначим допустимую область значений х, соответствующую ограничениям b — ? (х) = 0, через G. Тогда
. (17-12)
Область G в соотношении (17-12) образовывает часть от общей области трансформаций х, по которой ищется максимум в соотношении (17-11). Исходя из этого
h(?) ? h(?опт). (17-13)
Эта запись свидетельствует, что h(?) имеет минимум в точке ?опт. Но так как для х и ?, удовлетворяющих условию (17-22), h(?) = ? (х, ?), то выражение (17-13) говорит, что ? (x, ?) имеет минимум по ? в точке xопт при условии исполнения (17-10).
Задача минимизации ? (х, ?) по ? при ограничениях (17-10), каковые для каждого к определяют соответствующее х, именуется задачей, двойственной к задаче отыскания максимума F (х) при ограничениях ?i (х) = bi (i = 1, …, m):
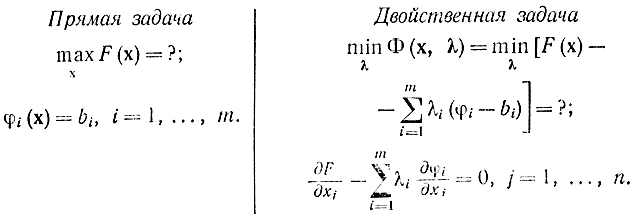
Двойственные задачи владеют тем свойством, что в окрестности хопт в соответствующих ограничениях
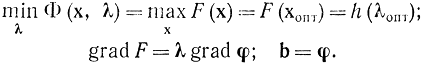
Но в соответствии с равенством (17-11)
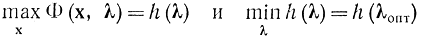
и исходя из этого
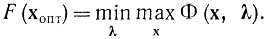
Это наиболее значимое соотношение свидетельствует, что задача оптимизации функции при ограничениях сводится к ответу задачи на минимакс. Оно смыкается с теорией игр и говорит, что задачи на условный экстремум сводятся к игровым задачам, в частности к отысканию седловой точки. Последнему утверждению возможно придать более четкую форму. В случае, если разглядывать малую окрестность точки [хопт, ?опт] в (n + m)-мерном пространстве, то потому, что ? (х, ?) имеет максимум по х, для любого ? из данной окрестности возможно написать:
? (х, ?опт) ? ? (xопт, ?опт) = F (хопт). (17-14)
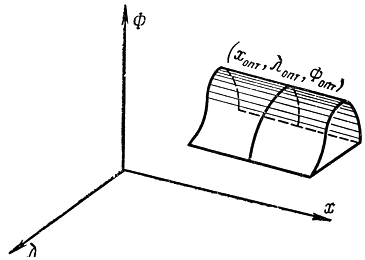
Рис. 17-7. Вырожденная седловая точка
Потом, ? (хопт, ?) = F (хопт), так как хопт ? G. Исходя из этого ? (хопт, ?) = F (хопт, ?). С учетом этого и соотношения (17-14) можем написать:
?(х, ?опт)? ?(xопт, ?опт) = Ф(хопт, ?)
Тем самым доказано, что функция Лагранжа имеет в оптимальной точке (хопт, ?опт) седловую точку, действительно, вырожденного типа, поскольку справа стоит символ строгого равенства (рис. 17-7; на нём перепутаны оси x и ? – так как ? неизменно по ?, а не по x).
Точка (хопт, ?опт) функции двух векторных переменных ? (х, ?) именуется седловой, в случае, если удовлетворяются соотношения
? (x, ?опт) ? ? (xoпт, ?опт) ? ?(xoпт, ?).
Хорошие способы оптимизации функции при наличии ограничений, так же как и хорошее вариационное исчисление, в принципе разрешают определять экстремум функции при ограничениях в виде нестрогих равенств, и, например, при требовании не отрицательности переменных. Но это сопряжено с возрастанием трудоемкости вычислений. Разглядим сначала случай не отрицательности переменных. Пускай имеется задача оптимизации вида
max{z=F(x)|x?0, ?i=bi, i=1,…,m; m
Допустим, что максимум достигается в точке хопт, которая лежит в либо на границе области допустимых значений. Первоначально исследуют все внутренние точки хорошего октанта n-мерного пространства и в них вычисляют значения функции цели z. После этого исследуют границу хорошего октанта, причем на первой стадии приравнивают нулю одну переменную, решают задачу на оптимум с оставшимися n–1 переменными, и m ограничениями и вычисляют значение функции цели для каждого решения. Так как переменных n, то на первой стадии нужно решить n задач с n–1 переменными и m ограничениями. На втором этапе приравнивают нулю каждые две координаты и решают задачу с n–2 переменными и m ограничениями. Возможно продемонстрировать, что число таких задач будет n!/2!/(n–2)!. В последующих задачах нулю приравниваются три, четыре и т. д. координаты. Из этого сходу видна трудоемкость для того чтобы вычислительного процесса. Если не все переменные подчинены условию не отрицательности, то нулю приравниваются лишь те, для которых это требование имеет место.
Сейчас разглядим случай, в то время, когда нет условий не отрицательности, но кое-какие из ограничений имеют форму неравенств. Пускай
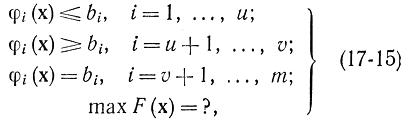
т. е. v ограничений имеют форму неравенств, остальные m–v — форму равенств. Добавим v переменных x?i?0 каковые сводят неравенства (17-15) к равенствам вида
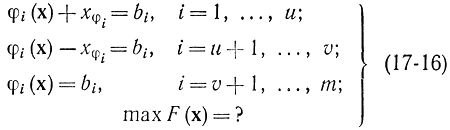
Сейчас задача свелась к ранее рассмотренной: ограничения заданы в виде строгих равенств, но имеется требование неотрицательности u + v переменных x?i. Увидим, что условие gi(x)?bi эквивалентно x?i?0 (i = 1, …, v), а условие gi (х)?bi эквивалентно x?i?0 (i = u + 1, …., vi). Экстремум может достигаться в неотрицательного октанта u-мерного пространства, где x?i0, и на его границах, где одно либо пара x?i=0. Разглядим сначала вариант с x?i0. Функция Лагранжа для уравнений (17-16) будет иметь вид:
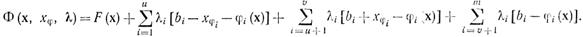
Для точки оптимума частные производные от данной функции по всем переменным, среди них и по x?i, должны равняться нулю. Исходя из этого
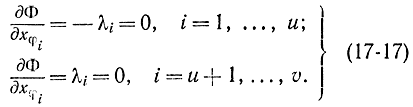
Эти соотношения означают, что в случае, если в точке экстремума x?i0, то соответствующие ?i = 0, т. е. ограничения, каковые в точке экстремума имеют вид строгих неравенств, возможно не учитывать. При перемещении по границе, где кое-какие x?i = 0, соответствующие ограничения направляться учитывать и для них ?i ? 0. По существу доказано крайне важное соотношение, что в точке оптимума либо вспомогательные переменные x?i = 0, либо соответствующие множители Лагранжа ?i = 0, т. е.
?iоптx?iопт = 0 (17-18)
либо
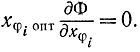
Так, сначала просматривают внутреннюю часть области хорошего октанта v-мерного пространства x?i, т. е. по существу отбрасывают все ограничения в форме неравенств (v штук), ищут ответ и вычисляют значение z. После этого поочередно подключают одно соотношение, эквивалентное x?i = 0, потом по два соотношения и т. д. и любой раз вычисляют значения z. Громаднейшее из этих z соответствует точке экстремума.
Выпуклое программирование
Интенсивное развитие нелинейного программирования в значительной мере позвано доказанной в 1951 г. фундаментальной теоремой Куна и Таккера о седловой точке в задачах выпуклого программирования. Эта теорема распространяет результаты о минимаксе, полученные в прошлом параграфе применительно к хорошему варианту для задач на условный экстремум, на случай задания ограничений в виде неравенств. Особенный интерес воображает эта теорема для недифференцируемых функций, о чем по большому счету не говорилось в хороших способах.
Сначала возьмём условия существования седловой точки у постоянной функции двух векторных переменных. После этого продемонстрируем, что эти условия удовлетворяются для оптимальной точки задачи нелинейного программирования.
Условия существования седловой точки. По определению функция ? (х, ?) двух векторных переменных х = || x1,…,xn || и ? = || ?1,…,?n|| имеет в точке (хопт, ?опт) седловую точку, в случае, если выполняются соотношения
? (х, ?опт) ? ? (хопт, ?опт) ? ? (хопт, ?) (17-19)
для всех х и ? из ?-окрестности (хопт, ?опт). Будем вычислять, что х?0 и ??0. Геометрически соотношение (17-19) интерпретируется посредством рис. 17-8 и 17-9. Наряду с этим допускается и вырожденный случай, в то время, когда в левой либо правой части стоит символ равенства.
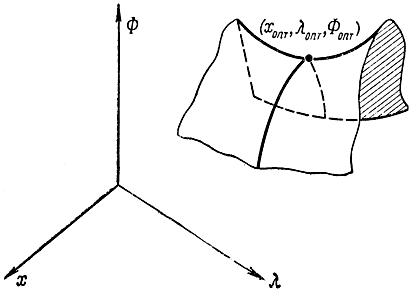
Рис. 17-8. Седловая точка
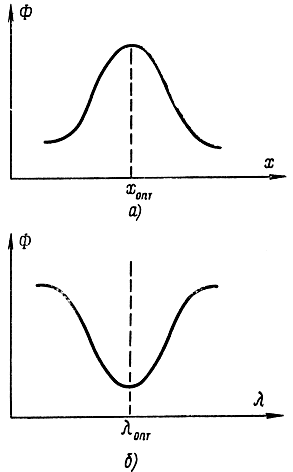
Рис. 17-9. Пояснение к седловой точке функции двух переменных
Докажем, что нужными и достаточными условиями существования седловой точки для функции двух векторных переменных являются соотношения
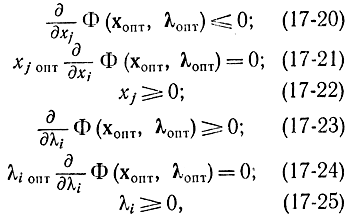
т. е. требуется доказать, что из условий (17-19) следуют (17-20) — (17-25) (необходимость) и из условий (17-20) — (17-25) следуют (17-19) (достаточность). Вправду, в случае, если при xj?0 предположить соотношения, обратные (17-20) и (17-21), т. е.
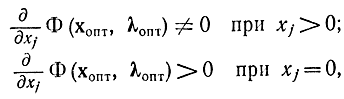
то это означало бы, что точка хопт при ? = ?опт не есть максимумом, поскольку для внутренних точек, где xj 0, в точке максимума обязана равняться нулю первая производная
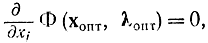
а на границе области, где xj = 0, первая производная для случая максимума должна быть не хороша, т. е.
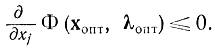
Наряду с этим подразумевается, что для внутренних точек, где xj0, соотношение (17-20) носит темперамент строгого равенства, а для граничных точек, где xj = 0, — темперамент неравенства. Соотношение (17-21) выполняется для внутренних точек за счет равенства нулю производной, а для граничных точек — за счет равенства нулю координаты.
Подобно доказывается необходимость условий (17-23) и (17-24) при 0, т. е. они следуют из условия минимизации функции ? (х, ?) довольно ?. То есть, поскольку функция ? (х, ?) при фиксированном хопт имеет минимум по ?, в точке ? = ?опт, то для внутренних точек ? 0 d?/d?i = 0, а для граничных ? = 0 d?/d?i ? 0.
Второй метод доказательства справедливости соотношений (17-23) и (17-24) возможно взять, в случае, если учесть, что при фиксированном х эта функция линейная довольно ?i. Вправду, в случае, если учесть, что
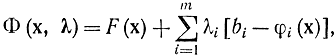
то соотношение (17-23) есть легко второй записью исходных ограничений
?i(x)?bi
так как
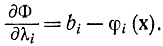
Как было продемонстрировано ранее [формулы (17-17) и (17-18)], в случае, если в окрестности точки экстремума bi — ?i(х)?0 и в точке экстремума bi — ?i(хопт) 0, то соответствующие ?iопт = 0. Для тех индексов i, при которых в точке экстремума (и малой окрестности ее) bi — ?i(х) = 0, ? (х, ?) = F (х), ?iопт ?0 (то есть ?i0). Исходя из этого в любой момент либо ?i= 0, либо d?/d?i = 0 и соотношение (17-18) выполняется.
Тем самым доказано, что из условий существования седловой точки (17-19) следуют соотношения (17-20) — (17-25). Дабы доказать их достаточность для существования седловой точки, предположим вогнутость (для максимума) функции ?(х, ?) по х и, разложив ее в ряд Тейлора, возьмём:
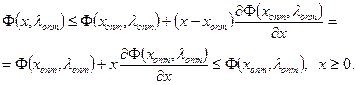(17-26)
В формуле (17-26) под производной d?(x,?)/dx, понимается градиент функции ? по х, т. е.
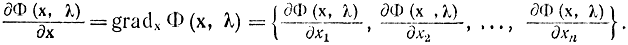
Разумеется, что для вогнутой функции в соответствии с рис. 17-10 значение ординаты, касательной вблизи точки вогнутости (хопт, ?опт), не меньше значения самой функции. Помимо этого, в случае, если сложить все равенства (17-21) по j, возьмём:
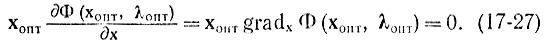
В соответствии с данной формулой в соотношении (17-26) честен символ равенства.
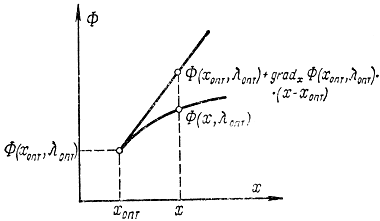
Рис. 17-10. Пояснение к разложению вогнутой функции в ряд Тейлора
И, наконец, в случае, если сложить по j все соотношения (17-20), возьмём:
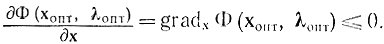
Исходя из этого в соотношении (17-26) при х?0 честен последний символ неравенства. Тем самым доказана левая часть соотношения (17-19), т. е. условие максимума функции ?(х, ?) по х в точке (хопт, ?опт). Подтверждение правой части данной формулы может выполняться двумя дорогами. Для любой выпуклой по к функции ? (х, ?) подобно соотношению (17-27) возможно написать:
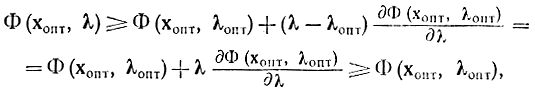
либо, учитывая линейность ? (х, ?) по ?,
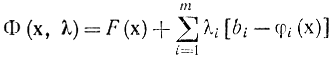
(и не предполагая выпуклости ее по ?), приобретаем:
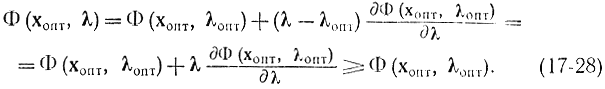
Первый символ равенства честен в силу линейности функции ? (хопт, ?) довольно ?. Второй символ равенства честен либо в силу соотношений (17-24), в случае, если их просуммировать по i, либо в силу уже использовавшихся рассуждений о том, что либо d?(х, ?)/d?i = 0, либо ?iопт = 0. Тем самым доказана правая часть соотношения (17-19) и достаточность условий (17-20)-(17-25) для существования седловой точки.
В случае, если имеется в виду седловая точка с минимумом по х и максимумом по ?, то соотношения (17-19) — (17-25) перепишутся в виде
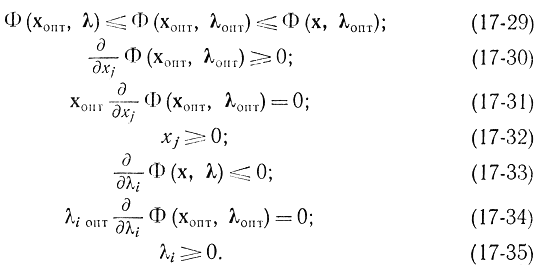
Теорема Куна-Таккера
Формулы (17-20)-(17-25) составляют содержание теоремы Куна — Таккера, лишь в отличие от прошлого параграфа, где функция Ф (х, Я) была произвольной, в этом случае она есть функцией Лагранжа для задачи максимизации нелинейного программирования, а (хопт, ?опт) — точка экстремума. Сама теорема возможно сформулирована следующим образом: соотношения (17-20)-(17-25) являются нужными и достаточными условиями, чтобы точка хопт представляла собой ответ задачи выпуклого нелинейного программирования:
max {F(x)|xj?0, j=1,…,n; ?i(х)?bi, i = 1,…,m}. (17-36)
Сведем исходную задачу к хорошей постановке. Для этого в первую очередь ограничения-неравенства ?i(х)?bi сведем к равенствам, введя и переменных x?i ?0 (i = 1,2,…, u), соответствующим неравенствам. Остальные m – u ограничений считаются строгими равенствами. Тогда
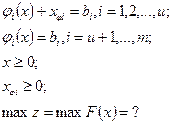
Тем самым допускается, что часть из m неравенств имеет форму строгих равенств.
Предположим, что для данной задачи х = хопт. Обозначим через J множество индексов j (j = 1, …, n) для которых xjопт 0, а через – множество индексов j, для которых xjопт = 0. Подобно будем вычислять, что I — множество индексов i (i = 1, …, u) для которых ?i(хoпт) = bi, – множество, складывающееся из индексов i, для которых ограничения на ?i(хопт) выполняются со знаком строгого неравенства ?i(xопт)4) либо в строгое равенство (типа 3=3). На основании результатов, взятых в § 17-3, можем написать, что
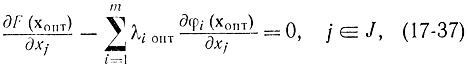
так как множество J соответствует внутренней области допустимых значений, и ?iопт = 0 , , так как множество I соответствует ограничениям в виде строгих неравенств, каковые возможно не учитывать. Потом
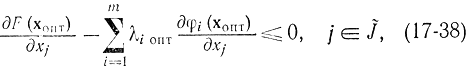
так как множество J соответствует границе области допустимых значений.
Соотношения (17-37) и (17-38) снабжают исполнение условия (17-20)
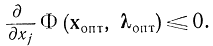
Сейчас нетрудно убедиться, что
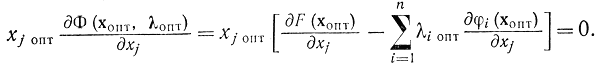
Это соотношение снабжает исполнение формулы (17-21). После этого имеем:
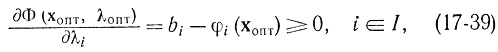
так как множество I соответствует границе области. Эти разности неотрицательны, а остальные n — u равны нулю по условию. Формула (17-39) снабжает исполнение условия (17-23), которое по существу сходится с ограничениями в исходной задаче нелинейного программирования. Наконец, условие (17-24) выполняется в силу доказанных ранее соотношений (17-17), в соответствии с которым для ограничений в виде строгих неравенств
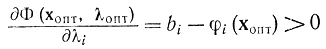
соответствующий множитель Лагранжа ?i = 0 и ?i ? 0 лишь при
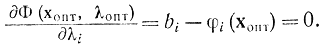
Так, доказано, что в точке оптимума задач нелинейного программирования выполняются нужные и достаточные условия существования седловой точки (необходимость теоремы Куна — Таккера). Для доказательства достаточности данной теоремы нужно дополнительно настойчиво попросить выпуклости (вогнутости) и применять способы доказательства достаточности условий (17-20) — (17-25) для существования седловой точки. Тем самым доказана теорема Куна — Таккера для случая дифференцируемых функций.
В литературе [Л. 96] имеются доказательства данной теоремы для не дифференцируемых функций F(х) и ?i(х). В этом случае теорема формулируется следующим образом: вектор хопт тогда и лишь тогда есть ответом задачи (17-36), в то время, когда существует вектор ?опт, таковой, что честны соотношения
? (xопт, ?) ? ? (xопт, ?опт) ? ? (х, ?опт) (17-41)
для всех х?0 и ??0, т. е. задача о максимизации F (х) соответствует задаче о седловой точке, иными словами, задаче о максимине для функции ? (х, ?).
ЕЩЁ О ТЕОРЕМЕ КУНА-ТАККЕРА
| Теорема 2.3. (Достаточное условие экстремума). В случае, если (х, и) — седловая точка функции Лагранжа, в области x?X?D, и?0,то х есть оптимальным замыслом задачи (2.28), причем справедливо так именуемое правило дополняющей нежесткости: |
Подтверждение.
По определению седловой точки
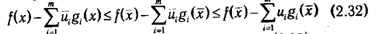
при всех x?X, и?0. Из второго неравенства в (2.32) направляться, что
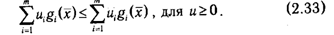
Но (2.33) может иметь место лишь тогда, в то время, когда gi(x)?0 при всех i?1:m. Вправду, в случае, если существует такое k, что gk(x)0, то, положив иi=0 для всех i ? k и выбрав большое иk 0, возможно добиться того, что значение
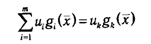
окажется больше постоянного выражения
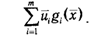
Из того, что для всех i?1:m выполняются неравенства gi(x)?0, направляться, что х есть допустимым замыслом задачи (2.28).
В случае, если в левую часть неравенства (2.33) подставить значения ui = 0, i?1:m, то возьмём, что
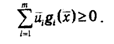
Вместе с тем из того что, gi(x)?0 и ui ?0, направляться оценка
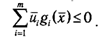
Совместное рассмотрение последних двух неравенств ведет к правилу дополняющей нежесткости в точке х:
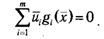
Тогда на основании левой части неравенства седловой точки (2.32) имеем, что для всех х?Х (среди них и для х?D)
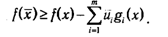
Но условию ЗНП для любых х?D верны неравенства gi(x)?0, что, в сочетании с условием ui ?0, разрешает записать
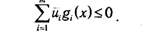
Значит,
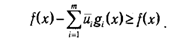
Совсем приобретаем, что для любых х?D справедливо соотношение f(x)?f(x), т. е. х — оптимальный замысел задачи (2.28). A
Перечень литературы
[1] Алексеев В. М., Тихомиров В. М., Фомин С. В., Оптимальное управление, Наука, М., 1979 MathSciNet MathSciNet
[2] Сухарев А. Г., Тимохов А. В., Федоров В. В., Курс способов оптимизации, Наука, М., 1986 MathSciNet MathSciNet Zentralblatt MATH
[3] Васильев Ф. П., Способы оптимизации, В 2-х кн., МЦНМО, М., 2011
[4] Мину М., Математическое программирование. алгоритмы и Теория, Наука, М., 1990 MathSciNet MathSciNet
[5] Обен Ж.-П., Нелинейный анализ и его экономические приложения, Мир, М., 1988 MathSciNet MathSciNet
[6] Обен Ж.-П., Экланд И., Прикладной нелинейный анализ, Мир, М., 1988 MathSciNet MathSciNet [7] Сумин М. И., “Регуляризованная параметрическая теорема Куна–Таккера в гиль- бертовом пространстве”, Ж. вычисл. матем. и матем. физ., 51:9 (2011), 1594– 1615 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH [8] Sumin M. I., “On the stable sequential Kuhn–Tucker theorem and its applications”, Appl. Math., 3:10A, Special issue “Optimization” (2012), 1334–1350 [9] Сумин М. И., “Оптимальное управление параболическими уравнениями: двой- ственные численные способы, регуляризация”, Распределенные совокупности: опти- мизация и приложения в науках и экономике об окружающей среде, Ин-т матем. и механ. УрО РАН, Екатеринбург, 2000, 66–69 [10] Сумин М. И., “Регуляризованный градиентный двойственный способ ответа об- ратной задачи финального наблюдения для параболического уравнения”, Ж. вы- числ. матем. и матем. физ., 44:11 (2004), 2001–2019 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH [11] Сумин М. И., “Регуляризация в линейно выпуклой задаче математического про- граммирования на базе теории двойственности”, Ж. вычисл. матем. и матем. физ., 47:4 (2007), 602–625 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH [12] Sumin M. I., “Parametric dual regularization in a linear-convex mathematical programming”, Comput. Optimizat. New Res. Developments, Ch. 10, Nova Sci. Publ. Inc., New–York, 2010, 265–311 [13] Варга Дж., Оптимальное управление дифференциальными и функциональными уравнениями, Наука, М., 1977 MathSciNet MathSciNet [14] Сумин М. И., “Регуляризованный двойственный способ ответа нелинейной за- дачи математического программирования”, Ж. вычисл. матем. и матем. физ., 47:5 (2007), 796–816 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH [15] Sumin M. I., “Parametric dual regularization in a nonlinear mathematical programming”, Ch. 5, Advances Math. Res., 11, Nova Sci. Publ. Inc., New–York, 2010, 103–134 [16] Borwein J. M., Strojwas H. M., “Proximal analysis and boundaries of closed sets in banach space. Part I: Theory”, Can. J. Math., 38:2 (1986), 431–452 crossref MathSciNet MathSciNet Zentralblatt MATH ; “Part II: Applications”, Can. J. Math., 39:2 (1987), 428–472 crossref Zentralblatt MATH [17] Кларк Ф., негладкий анализ и Оптимизация, Наука, М., 1988 MathSciNet MathSciNet Zentralblatt MATH [18] Loewen P. D., Optimal control via nonsmooth analysis, CRM Proc. Lecture Notes, 2, Amer. Math. Soc., Providence, RI, 1993 MathSciNet MathSciNet Zentralblatt MATH
А. В. Верёвок, М. И. Сумин Секвенциальная устойчивая теорема Куна–Таккера в нелинейном программировании Издание вычислительной математики и математической физики, 2013, 53:8, 1249–1271