Главные действия над матрицами
Матрица может состоять как из одной строки, так и из одного столбца. По большому счету говоря, матрица может состоять кроме того из одного элемента. Определение. В случае, если число столбцов матрицы равно строчков (m=n), то матрица именуется квадратной. Определение. Матрица вида.(100)
(010)
(001)
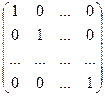= E,
именуется единичной матрицей.
Определение. В случае, если amn = anm , то матрица именуется симметрической.
Пример.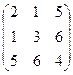 
— симметрическая матрица
Определение.Квадратная матрица вида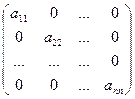 
именуется диагональнойматрицей.
вычитание и Сложение матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций есть то, что они выяснены лишь для матриц однообразного размера. Так, допустимо выяснить вычитания матриц и операции сложения:
Определение. Суммой (разностью) матриц есть матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
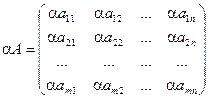
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример. Даны матрицы А =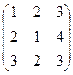 
; B =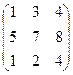 
, отыскать 2А + В.
2А =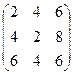 
, 2А + В = 
.
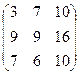Операция умножения матриц
Определение: Произведением матриц именуется матрица, элементы которой смогут быть вычислены по следующим формулам:
A?B = C;
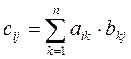
Из приведенного определения видно, что операция умножения матриц выяснена лишь для матриц, число столбцов первой из которых равно строчков второй.
Свойства операции умножения матриц.
1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА кроме того в случае, если выяснены оба произведения. Но, в случае, если для каких – или матриц соотношение АВ=ВА выполняется, то такие матрицы именуются перестановочными.
Самым характерным примером может служить единичная матрица, которая есть перестановочной с каждый матрицей того же размера.
Перестановочными смогут быть лишь квадратные матрицы одного и того же порядка.
А?Е = Е?А = А
Разумеется, что для любых матриц выполняются следующее свойство:
A?O = O; O?A = O,
где О – нулеваяматрица.
2) Операция перемножения матриц ассоциативна, т.е. в случае, если выяснены АВ и произведения (АВ)С, то выяснены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. в случае, если имеют суть выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) В случае, если произведение АВ выяснено, то для любого числа a правильно соотношение:
a(AB) = (aA)B = A(aB).
5) В случае, если выяснено произведение АВ , то выяснено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Увидим кроме этого, что для любых квадратных матриц det (AB) = detA?detB.
Транспонированная матрица
Определение. Матрицу В именуют транспонированнойматрицей А, а переход от А к В транспонированием, в случае, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А =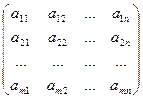 
; В = АТ= 
;
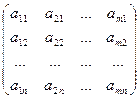иначе говоря bji = aij.
В качестве следствия из прошлого свойства (5) возможно записать, что:
(ABC)T = CTBTAT,
при условии, что выяснено произведение матриц АВС.
Пример. Даны матрицы А =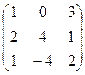 
, В = , С = 
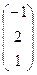и число a = 2. Отыскать АТВ+aС.
AT =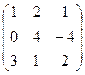 
; ATB = ? = 
= 
;
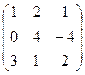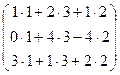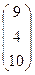aC =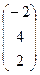 
; АТВ+aС = + = 
.
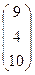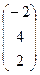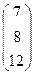Пример. Отыскать произведение матриц А = и В = .
АВ = ? =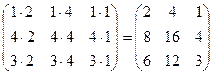 
.
ВА = ? = 2?1 + 4?4 + 1?3 = 2 + 16 + 3 = 21.
Пример. Отыскать произведение матриц А= , В =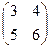 
АВ = ? = = .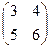
Обратная матрица
Определим операцию деления матриц как операцию, обратную умножению.
Определение.В случае, если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е — единичная матрица того же самого порядка, что и матрица А, то матрица Х именуется обратнойк матрице А и обозначается А-1.
Любая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом лишь одну.
Разглядим неспециализированный подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, возможно записать:
AX = E ?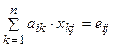 
, i=(1,n), j=(1,n),
eij = 0, i ¹ j,
eij = 1, i = j .
Так, приобретаем совокупность уравнений:
,
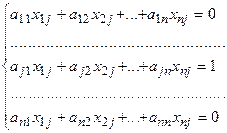Решив эту совокупность, находим элементы матрицы Х.
Пример. Дана матрица А =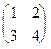 
, отыскать А-1.
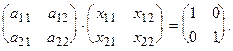
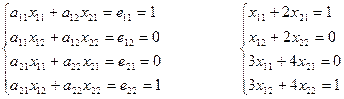
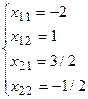
Так, А-1=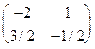 
.
Но, таковой метод не эргономичен при нахождении обратных матриц громадных порядков, исходя из этого в большинстве случаев используют следующую формулу:
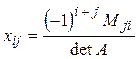
где Мji- дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = 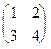, отыскать А-1.
det A = 4 — 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Так, А-1= .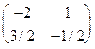
Cвойства обратных матриц
Укажем следующие особенности обратных матриц:
1) (A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T.
Пример. Дана матрица А =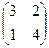 
, отыскать А3.
А2 = АА = =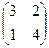 
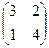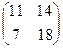; A3 = =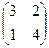 
.
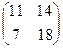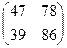Напомним, что матрицы 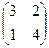и 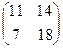являются перестановочными.
Пример. Вычислить определитель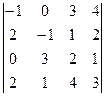 
.
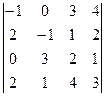= -1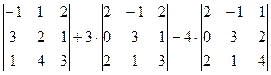 
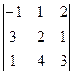= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.
= 
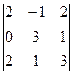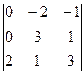= 2(0 – 2) – 1(0 – 6) = 2.
= 
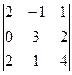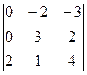= 2(-4) – 3(-6) = -8 + 18 = 10.
Значение определителя: -10 + 6 – 40 = -44.
Ранг матрицы
Определение. Определение. Рангом матрицы именуется наивысший порядок хороших от нуля миноров. Т.е. в случае, если у матрицы порядка (m, n) имеется хороший от нуля минор порядка r,
r
Весьма серьёзным свойством элементарных преобразований матриц есть то, что они не изменяют ранг матрицы.
Элементарные преобразования матрицы
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строчка на число, хорошее от нуля;
2) прибавление к элемнтам одной строки элементов второй строки;
3) перестановка строчков;
4) вычеркивание (удаление) одной из однообразных строчков (столбцов);
5) транспонирование;
Те же операции, используемые для столбцов, кроме этого именуются элементарными преобразованиями.
Посредством элементарных преобразований возможно к какой-либо строке либо столбцу прибавить линейную комбинацию остальных строчков ( столбцов ).
. РАНГ СТУПЕНЧАТОЙ МАТРИЦЫ РАВЕН ЧИСЛУ ЕЕ СТРОЧКОВ
Арифметическим вектором именуется упорядоченная совокупность n чисел.
Обозначается x = (x1, x2, …, xn);
числа x1, x2, …, xn именуются компонентами арифметического вектора.
Для арифметических векторов выяснены линейные операции — сложение арифметических векторов и умножение вектора на число:
для любых x = (x1, x2, …, xn), y = (y1, y2, …, yn) и любого числа ? справедливо:
x + y = (x1+ y1, x2 +y2, …, xn+ yn);?x = (?x1, ?x2, …, ?xn).
Множество арифметических векторов, для которых выяснены умножения и операции сложения на число именуется пространством арифметических векторов Rn.
Вектор ? = (0, 0, …, 0) именуется нулевым вектором Rn,
а вектор ?x = (?x1, ?x2, …, ?xn) — противоположным вектором для вектора xвRn.
Для любых векторов x, y и zиз Rn и любых чисел ? и ? справедливо:
1. x + y = x + y, сложение коммутативно;
2. x + (y + z) = (x + y)+ z, сложение ассоциативно;
3. x + ? = x;
4. x + (?x) = ?;
5. ?(x + y) = ?x + ?y, умножение на число дистрибутивно относительно сложения векторов;
6. ?(?x) = (??)x, умножение на число ассоциативно;
7. (? + ?)x = ?x + ?x , умножение вектора на число дистрибутивно относительно сложения чисел.
8. 1·x = x.
Пространство Rn ? n-мерное векторное пространство, dimRn = n.
В случае, если в пространстве Rn выяснен естественный базис e1, e2, … en ,
e1= (1, 0, 0,…, 0, 0), e2= (0, 1, 0,…, 0, 0), …, en-1= (0, 0, 0,…, 1, 0), en= (0, 0, 0,…, 0, 1),
то компоненты вектора x = (x1, x2, …, xn) из Rn являются координатами вектора x в естественном базисе e1, e2, … en:
x = (x1, x2, …, xn) = x1e1+ x2e2+ …+ xnen.
Всякое конечномерное n-мерное линейное пространство изоморфно пространству арифметических векторов Rn.
Пример
L ? множество 6-мерных арифметических векторов, у которых чётные коомпоненты равны нулю, {x =(x1, 0, x2, 0, x5, 0 )} ? трёхмерное линейное пространство, изоморфное пространству арифметических векторов R3.
Вправду.
Как видно из вышеприведенных соотношений, множество L ? трёхмерное линейное пространство (три вектора e1, e2и e3 образуют базис), изоморфное пространству трёхмерных арифметических векторов R3.
Теорема. В произвольной матрице А любой столбец (строчок) есть линейной комбинацией столбцов (строчков), в которых расположен базовый минор.
Так, ранг произвольной матрицы А равен большому числу линейно свободных строчков (столбцов) в матрице.
В случае, если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов — линейная комбинация остальных столбцов. То же самое справедливо и для строчков. Данное утверждение направляться из свойства линейной зависимости при определителе равном нулю
Способ Гаусса для ответа совокупностей линейных уравнений.
Процесс ответа складывается из двух этапов. В первом совокупность приваодят к ступенчатому виду. Во втором решают ступенчатую совокупность. В случае, если ступенчатая совокупность оказывается треугольной, то исходная совокупность имеет единственное ответ.
Формулы Крамера. Ответ неоднородной совокупности уравнений с малоизвестными, имеющей невырожденную главную матрицу совокупности, находится по формулам
,
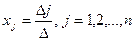где — определитель совокупности; — определитель матрицы, приобретаемой из главной матрицы совокупности заменой её -го столбца столбцом свободных участников.
Примеры
1. Решить совокупность уравнений
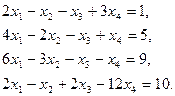
Ответ. Будем решать способом Гаусса. Выпишем расширенную матрицу совокупности и преобразуем её, вычитая первую строчок, умноженную на 2, 3 и 1 соответственно из 2-ой, 3-ей и 4-ой строчков:
.
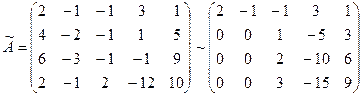Потом вторую строчок, умноженную на 2 и 3, вычтем соответственно из четвёртой строк и третей:
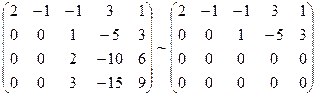
Последняя матрица эквивалентна следующей ступенчатой совокупности:
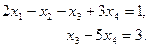
Полученная упрощённая совокупность является системой из двух уравнений для четырёх малоизвестных. Следовательно, два из малоизвестных возможно выбрать за главные, а два — за свободные, через каковые будут выражены главные. В качестве основных малоизвестных возможно выбрать любую несколько, в случае, если определитель, составленный из коэффициентов, стоящих перед ними, отличен от нуля (базовый
минор). В данной задаче в качестве основных малоизвестных возможно выбрать .
Вправду, определитель, составленный из их коэффициентов, отличен от нуля:
.
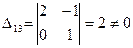Сейчас из второго уравнения выразим через . После этого подставим его в первое уравнение и отыщем через . В итоге возьмём
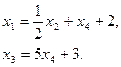
Переменные принимают произвольные значения. Положив , неспециализированное ответ совокупности возможно записать в виде
.
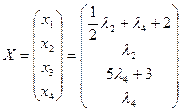Совокупность уравнений
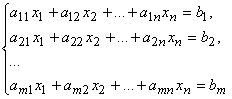
относительна малоизвестных x1, x2, …, xn-1, xn именуется совокупностью линейных алгебраических уравнений.
Числа aij — коэффициенты совокупности, bi— правые части совокупности i = 1, 2, …, m; j = 1, 2, …, n.
Совокупность значений малоизвестных, удовлетворяющая всем уравнениям совокупности, именуется ответом совокупности.
Совокупность, имеющая хотя бы одно ответ, именуется совместной. Совокупность, у которой нет ответов, именуется несовместной.
Каждое ответ совместной совокупности именуется частным ответом. Совокупность всех ответов совместной совокупности именуется неспециализированным ответом.
В случае, если среди правых частей bi совокупности имеется хоть одна, хорошая от нуля, то совокупность именуется неоднородной совокупностью линейных уравнений.
В случае, если все правые части совокупности равны нулю, то совокупность именуется однородной.
Совокупность линейных уравнений возможно записана в матричной форме A·x = b:
Тут A — матрица совокупности, b — правая часть совокупности , x— искомое ответ совокупности.
Время от времени комфортно записывать совокупность линейных уравнений в второй матричной форме:
A(1)x1 + A(2)x2 + … + A(n)xn = b.
Тут A(1), A(2), … , A(n) — столбцы матрицы совокупности.
Матрица Ap именуется расширенной матрицей совокупности.
В случае, если исследуется неоднородная совокупность A·x = b, b ? 0, то совокупность A·x =0именуется приведенной однородной совокупностью для совокупности A·x = b.
Две совокупности довольно одних и тех же малоизвестных эквивалентны, в случае, если множества их ответов совпадают.
Совокупности A·x = b и B·A·x =B·b эквивалентны, в случае, если матрица B невырождена
Примеры линейных пространств.
1). Пространства и ,складывающиеся из всевозможных (упорядоченных) комплектов из n чисел (соответственно — настоящих либо комплексных). умножение и Сложение определяются формулами
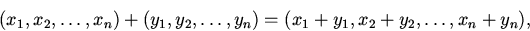
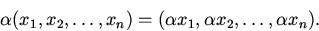
С этими пространствами вы достаточно отлично привычны по направлениям анализа и алгебры.
2). Постоянные (настоящие либо комплексные) функции на некоем отрезке [a, b] с простыми операциями умножения и сложения функций их на числа образуют линейное пространство C[a, b], являющееся одним из наиболее значимых в анализе и уже видевшееся вам, к примеру, при изучении функциональных последовательностей.
3). Пространство быстроубывающих функций 
,с которым вы трудились, изучая преобразование Фурье.
4). Пространство l2, в котором элементами помогают последовательности чисел (настоящих либо комплексных)
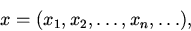
удовлетворяющие условию
с операциями
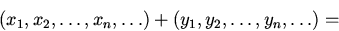
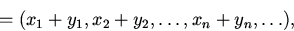
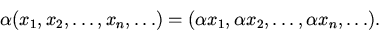
есть линейным пространством. Тот факт, что сумма двух последовательностей, удовлетворяющих условию (1), кроме этого удовлетворяет этому условию, вытекает из элементарного неравенства
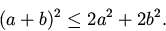
Конечный комплект элементов линейного пространства L именуется линейно зависимым, а сами элементы — линейно зависимыми, в случае, если существуют такие числа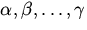 
,не все равные нулю, что
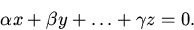
В другом случае эти элементы именуются линейно свободными. Иными словами, элементы именуются линейно свободными, в случае, если из равенства
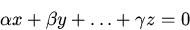
вытекает, что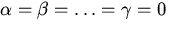 
.
Нескончаемая совокупность элементов пространства L именуется линейно свободной, в случае, если каждая ее конечная система линейно свободна.
В случае, если в пространстве L возможно отыскать n линейно свободных элементов, а каждые n+1 элементов этого пространства линейно зависимы, то говорят, что L имеет размерность n. В случае, если же в L возможно указать совокупность из произвольного конечного числи линейно свободных элементов, то говорят, что пространство L бесконечномерно.
Легко понять, что в вышеприведенных примерах 2)-4) пространства бесконечномерны, а в примере 1) — имеют размерность n.
Непустое подмножество L’ линейного пространства L именуется подпространством, если оно само образует линейное пространство по отношению к опрелеленным в L операциям умножения и сложения на число.
В противном случае говоря,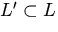 
имеется подпространство, в случае, если из 
, 
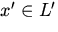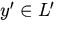направляться, что 
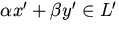при любых числах 
.
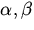В случае, если каждой паре векторов x, y линейного пространства L поставлено в соответствие настоящее число (x, y), так, что для любых x, y и z из L и любого настоящего числа ? честны следующие теоремы:
(x, y) = (y, x),
(?·x, y) = ?·(x, y),
(x + y, z) =(x, z) + (y, z),
(x, x) 0 при x ? 0, (0, 0) = 0,
то в пространстве L выяснено скалярное произведение (x, y).
В случае, если в линейном пространстве выяснено скалярное произведение, то такое пространство именуется евклидовым пространством.
Евклидовы пространства E и E’ именуются евклидово изоморфными, если они изоморфны как линейные пространства и в случае, если
x ?E, y ?E, x x’ ?E’, y y’ ?E’, то (x, y) = (x’, y’).
Главные действия над матрицами
Матрица может состоять как из одной строки, так и из одного столбца. По большому счету говоря, матрица может состоять кроме того из одного элемента. Определение. В случае, если число столбцов матрицы равно строчков (m=n), то матрица именуется квадратной. Определение. Матрица вида.(100)
(010)
(001)
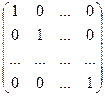= E,
именуется единичной матрицей.
Определение. В случае, если amn = anm , то матрица именуется симметрической.
Пример. 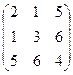— симметрическая матрица
Определение.Квадратная матрица вида 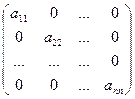именуется диагональнойматрицей.
вычитание и Сложение матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций есть то, что они выяснены лишь для матриц однообразного размера. Так, допустимо выяснить вычитания матриц и операции сложения:
Определение. Суммой (разностью) матриц есть матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
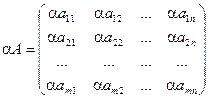
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Пример. Даны матрицы А = 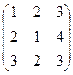; B = , отыскать 2А + В.
2А = 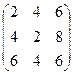, 2А + В = .
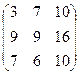Операция умножения матриц
Определение: Произведением матриц именуется матрица, элементы которой смогут быть вычислены по следующим формулам:
A?B = C;
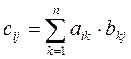
Из приведенного определения видно, что операция умножения матриц выяснена лишь для матриц, число столбцов первой из которых равно строчков второй.
Свойства операции умножения матриц.
1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА кроме того в случае, если выяснены оба произведения. Но, в случае, если для каких – или матриц соотношение АВ=ВА выполняется, то такие матрицы именуются перестановочными.
Самым характерным примером может служить единичная матрица, которая есть перестановочной с каждый матрицей того же размера.
Перестановочными смогут быть лишь квадратные матрицы одного и того же порядка.
А?Е = Е?А = А
Разумеется, что для любых матриц выполняются следующее свойство:
A?O = O; O?A = O,
где О – нулеваяматрица.
2) Операция перемножения матриц ассоциативна, т.е. в случае, если выяснены АВ и произведения (АВ)С, то выяснены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. в случае, если имеют суть выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) В случае, если произведение АВ выяснено, то для любого числа a правильно соотношение:
a(AB) = (aA)B = A(aB).
5) В случае, если выяснено произведение АВ , то выяснено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Увидим кроме этого, что для любых квадратных матриц det (AB) = detA?detB.
Транспонированная матрица
Определение. Матрицу В именуют транспонированнойматрицей А, а переход от А к В транспонированием, в случае, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А = 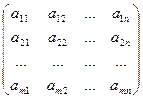; В = АТ= ;
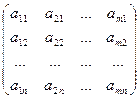иначе говоря bji = aij.
В качестве следствия из прошлого свойства (5) возможно записать, что:
(ABC)T = CTBTAT,
при условии, что выяснено произведение матриц АВС.
Пример. Даны матрицы А = 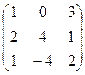, В = , С = 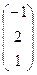и число a = 2. Отыскать АТВ+aС.
AT = 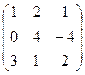; ATB = ? = = ;
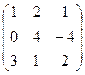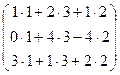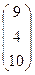aC = 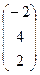; АТВ+aС = + = .
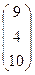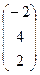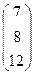Пример. Отыскать произведение матриц А = и В = .
АВ = ? = .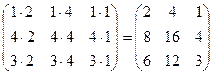
ВА = ? = 2?1 + 4?4 + 1?3 = 2 + 16 + 3 = 21.
Пример. Отыскать произведение матриц А= , В =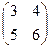
АВ = ? 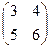= = .