Матричная запись . Расширенная матрица отличается от матрицы самой совокупности наличием нулевого столбца, т.е. ранг матрицы равен рангу расширенной матрицы : .. Значит, по теореме Кронекера-Капелли, совокупность однородных линейных уравнений в любой момент совместна. Одно ответ разумеется: . Это решение именуется тривиальным. Следуя потом теореме Кронекера-Капелли, приходим к выводу, что в случае, если , то ответ единственное — тривиальное. В случае, если , то ответов нескончаемое множество.
ТЕОРЕМА. Чтобы совокупность однородных уравнений имела решения, хорошие от нулевого, нужно и достаточно, дабы ранг матрицы совокупности был меньше числа малоизвестных.
Иначе говоря в случае, если число уравнений равно малоизвестных, то совокупность имеет ненулевое ответ тогда и лишь тогда, в то время, когда . Очевидны следующие особенности ненулевого ответа.
1) В случае, если – ответ, то – также ответ.
2) В случае, если – решения, то и – также решения.
В конечном итоге этих особенностей возможно убедиться яркой подстановкой. Обозначим главные малоизвестные через . Тогда 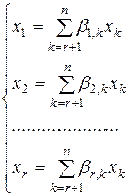 . В матричной форме:
. В матричной форме: 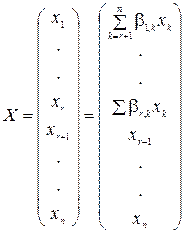 .
.
Возможно записать так:
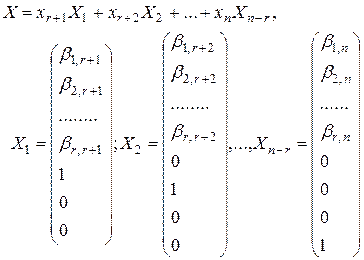
Ответы именуются фундаментальной совокупностью ответов (ФСР) однородной совокупности. Неспециализированное ответ совокупности есть линейной комбинацией фундаментальной совокупностью ответов .
Типовые примеры
Отыскать неспециализированное ответ совокупности.
1) 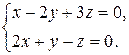
Эта совокупность apriori есть совместной, т.к. она однородна (все свободные члены равны нулю). Однородная совокупность постоянно имеет нулевое (либо тривиальное) ответ: . Для однородных совокупностей особенный интерес воображает вопрос о существовании ненулевых (либо нетривиальных) ответов. Так именуют всякое ответ совокупности, у которого значение хоть одного малоизвестного превосходно от нуля.
Преобразуем расширенную матрицу совокупности:
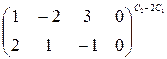 ~
~ 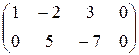 .
.
Имеем – совокупность совместна. Тогда – количество свободных малоизвестных. Полагая (где – произвольная постоянная), возьмём
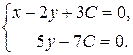
Из этого 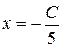 ,
, 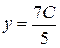 . Так, неспециализированное ответ совокупности имеет форму
. Так, неспециализированное ответ совокупности имеет форму
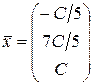 , где – произвольная постоянная.
, где – произвольная постоянная.
2) Отыскать общее решение и фундаментальную совокупность совокупности уравнений
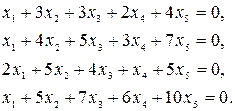
Выпишем матрицу совокупности и упростим её посредством элементарных преобразований, вычитая первую строчок, умноженную на 1,2 и 1 соответственно из второй, третьей и четвёртой строчков:
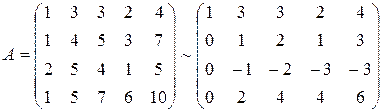 .
.
Сейчас вторую строчок прибавим к третьей и её же, умноженную на 2, вычтем из четвёртой строки, возьмём
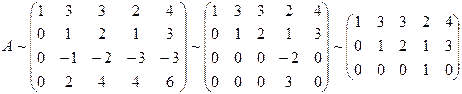
Ранг данной матрицы равен трём. Следовательно, три малоизвестные являются главными, а две — свободными. Выберем в качестве основных . Это возможно сделать, т.к. минор 3-го порядка, составленный из коэффициентов при этих малоизвестных, отличен от нуля. Соответствующая преобразованной матрице совокупность имеет форму
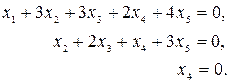
Из этого, высказывая главные малоизвестные через свободные, возьмём неспециализированное ответ
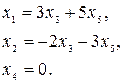
Дабы записать фундаментальную совокупность ответов (ФСР), нужно из вектор-столбца 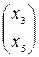 составить любым методом два линейно свободных вектора. В большинстве случаев это делается методом задания искомого вектор-столбца в виде столбцов единичной матрицы размером, равным высоте столбца из свободных малоизвестных. В этом случае – это матрица второго порядка
составить любым методом два линейно свободных вектора. В большинстве случаев это делается методом задания искомого вектор-столбца в виде столбцов единичной матрицы размером, равным высоте столбца из свободных малоизвестных. В этом случае – это матрица второго порядка
 .
.
Придавая значения из первого и второго столбцов данной матрицы, возьмём ФСР:
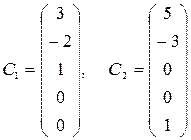 .
.
Потому, что неспециализированное ответ совокупности имеется сумма линейно свободных ответов из ФСР, умноженных на произвольные коэффициенты, то его возможно записать ещё в следующем виде: 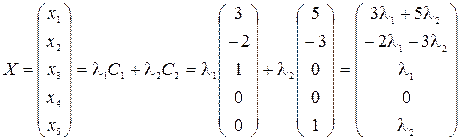 .
.
Как мы отмечали ранее, совокупность линейных уравнений может или вовсе не иметь ответов, или иметь единственное ответ, или иметь их пара (в последнем случае, выясняется, совокупность постоянно имеет нескончаемое множество ответов). Это утверждение исчерпывает все вероятные обстановки. При изложении (на примерах) способа Гаусса мы взяли возможность эвристически дать ответ на вопрос о числе ответов (при совместности совокупности). Строгий ответ на данный вопрос дает следующая теорема.
ТЕОРЕМА(о числе ответов). Пускай для совокупности линейных уравнений с малоизвестными выполнено условие совместности, т.е. ранг матрицы совокупности равен рангу ее расширенной матрицы. Тогда, в случае, если ранг матрицы совокупности равен числу малоизвестных ( ), то совокупность имеет единственное ответ. В случае, если же ранг матрицы совокупности меньше числа малоизвестных ( ), то совокупность имеет нескончаемое множество ответов, то есть: некоторым малоизвестным возможно придавать произвольные значения, тогда оставшиеся малоизвестных определятся уже единственным образом.
Пример
Затраты трех видов сырья (А,В,С) на производство единицы каждого из трех типов продукции (I,II,III) и запасы каждого типа сырья даны в табл. 8.
Таблица 8
| Вид сырья | Тип продукции I II III | Запасы сырья | ||
| А | ||||
| В | ||||
| С |
Выяснить замысел производства, снабжающий применение всего сырья. Составить математическую модель задачи и решить совокупность матричным способом.
Пускай предприятие выпустит единиц — продукции I, единиц — продукции II, единиц -продукции III. — расход сырья на все виды продукции. По условию задачи расход сырья обязан равняться запасу 220, т.е. . Подобно, приравнивая запасы и расходы сырья и , приобретаем совокупность уравнений
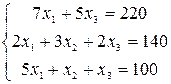 .
.
Обозначим = 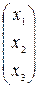 -матрица количеств выпуска I, II, III типов продукции.
-матрица количеств выпуска I, II, III типов продукции.
= 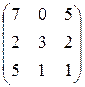 — матрица затрат ресурсов, =
— матрица затрат ресурсов, = 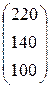 – матрица запасов ресурсов. Систему решим матричным методом. Имеем
– матрица запасов ресурсов. Систему решим матричным методом. Имеем
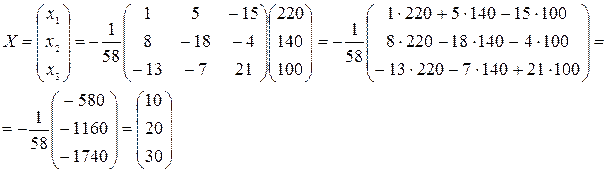
Следовательно, .
Пример
Из некоего листового материала нужно выкроить 360 заготовок типа , 300 заготовок типа и 675 заготовок типа . Наряду с этим возможно использовать три метода раскроя. Количество заготовок, приобретаемых из каждого страницы при каждом методе раскроя, указано в табл. 9.
Таблица 9
| Тип | Метод раскроя | ||
| заготовки | |||
| А | |||
| В | |||
| С |
Записать в математической форме условия исполнения задания.
Обозначим через количество страниц материала, раскраиваемых соответственно первым, вторым и третьим методами. Тогда при первом методе раскроя страниц будет получено заготовок типа , при втором — , при третьем — .
Для полного исполнения задания по заготовкам типа сумма обязана равняться 360, т.е.
.
Подобно приобретаем уравнения
,
,
которым должны удовлетворять малоизвестные чтобы выполнить задание по заготовкам и . Система линейных уравнений и высказывает в математической форме условия исполнения всего задания по заготовкам , и . Решим данную совокупность. Вектор 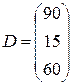 имеется ответ совокупности.
имеется ответ совокупности.
Пример
Три судна доставили в порт 6000 т чугуна, 4000 т металлической руды и 3000 т апатитов. Разгрузку возможно создавать как конкретно в ЖД вагоны для доставки потребителям, так и на портовые склады. В вагоны возможно разгрузить 8000 т, а остаток груза нужно будет направить на склады. Нужно учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Цена выгрузки 1 т в вагоны образовывает соответственно 4,30, 5,25 и 2,20 ден. ед. Записать в математической форме условия полной разгрузки судов, в случае, если затраты на нее должны составить 58850 ден. ед.
По условию задачи, доставленные в порт чугун, апатиты и железную руду возможно разгрузить двумя методами: или в ЖД вагоны, или в портовые склады. Обозначим через количество груза (в тоннах) -го вида ( ), которое предполагается разгрузить -м методом ( ). Так, задача содержит шесть малоизвестных. Условие полной разгрузки чугуна возможно записать в виде
,
где , — части чугуна, разгружаемого соответственно в вагоны и на склады. Подобное условие должно выполняться и для металлической руды:
.
Что же касается апатитов, то их возможно разгружать лишь на склады, а исходя из этого малоизвестное , и условие полной разгрузки апатитов принимает вид
.
Условие полной загрузки всех поданных в порт вагонов запишется так:
Затраты на разгрузку, по условию, выяснены в 58850 ден. ед., что возможно выразить записью:
.
Итак, с учетом сложившейся в порту обстановки условия полной разгрузки судов выражаются в математической форме системой линейных уравнений. С учетом того, что имеем:
,
и сейчас мы имеем совокупность из четырех уравнений с четырьмя малоизвестными , расширенная матрица которой имеет форму:
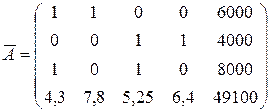
Ответ данной совокупности: , , , .
Пример
Затраты на автомобильном транспорте выражаются формулой , а на ЖД — , где — расстояние в километрах, — транспортные затраты на 1 км. (в усл.ден.ед.). Выстроить графики функций, произвести экономический анализ, вычислить транспортные затраты при км.
Выстроим прямые (I) и (II).
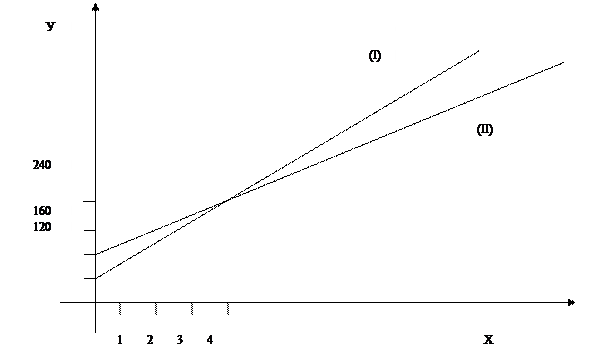
Отыщем точку пересечения двух прямых: 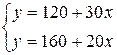 , .
, .
В случае, если , оба вида транспорта эквивалентны по затратам. В случае, если , автомобильные перевозки удачнее, а при удачнее становятся ЖД перевозки. Вычислим транспортные затраты при км. (усл. ден. ед.) — затраты на автомобильном транспорте; (усл. ден. ед.) — затраты на ЖД транспорте.
Пример
Математическая модель межотраслевого баланса.
Модель межотраслевого баланса, созданная доктором наук В. Леонтьевым (Гарвардский университет, США), имеет форму:
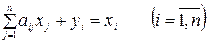
либо, в матричной форме,
где — матрица коэффициентов прямых затрат (коэффициентов материалоемкости), — вектор валовых выпусков, — вектор конечного продукта. Количество продукции -той отрасли, расходуемый -той отраслью в ходе производства — . Чистой продукцией отрасли именуется разность между валовой продукцией данной отрасли и затратами продукции всех отраслей на производство данной отрасли.
Перепишем данную совокупность в виде
где — единичная матрица -го порядка, тогда ответ совокупности довольно малоизвестных значений количеств производства продукции при заданном векторе конечного продукта находится по формуле
.
Тут — матрица коэффициентов полных затрат. Элемент матрицы характеризует потребность в валовом выпуске отрасли , что нужен для получения в ходе материального производства единицы конечного продукта отрасли . Именно поэтому имеется возможность разглядывать валовые выпуски в виде функций планируемых значений конечных продуктов отраслей:
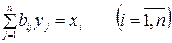 .
.
В соответствии с экономическим смыслом задачи значения при и .
Матрица (все ) именуется продуктивной, в случае, если для любого вектора (все ) существует ответ уравнения -вектор таковой, что все . При таких условиях и модель Леонтьева именуется продуктивной.
ТЕОРЕМА 1. В случае, если для матрицы с неотрицательными элементами и некоего вектора с неотрицательными элементами уравнение имеет ответ с неотрицательными компонентами, то матрица продуктивна.
Так для продуктивности матрицы достаточно установить наличие хорошего ответа уравнения хотя бы для одного хорошего вектора . Наряду с этим ответ находится по формуле .
ТЕОРЕМА 2 (первый критерий продуктивности – нужное и достаточное условие продуктивности). Матрица с неотрицательными элементами продуктивна тогда и лишь тогда, в то время, когда матрица существует и ее элементы неотрицательны.
ТЕОРЕМА 3 (второй критерий продуктивности – достаточное условие продуктивности). Матрица с неотрицательными элементами продуктивна, в случае, если сумма элементов по любому ее столбцу (строчке) не превосходит единицы, т.е. 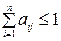 , причем хотябы для одного столбца (строчка) эта сумма меньше единицы.
, причем хотябы для одного столбца (строчка) эта сумма меньше единицы.
Пример
Пускай дана леонтьевская балансовая модель «затраты – выпуск» . Отыскать вектор конечной продукции при заданном , где
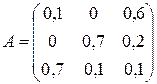 ;
; 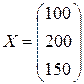 .
.
Имеем: , где — единичная матрица третьего порядка.
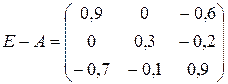 , значит,
, значит, 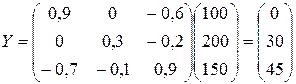 .
.
Пример
Изучить на продуктивность следующие матрицы: 1) 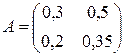 ; 2)
; 2) 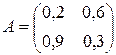 .
.
1) Для матрицы выполнены условия второго критерия продуктивности: сумма элементов каждого столбца матрицы меньше единицы. Следовательно, эта матрица есть продуктивной.
2) В этом случае условия второго критерия продуктивности для матрицы не выполняются, поскольку сумма элементов первого столбца матрицы больше единицы. Удостоверимся в надежности условия первого критерия матрицы продуктивности. Отыщем матрицу : 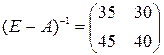 . Так как все элементы взятой матрицы неотрицательны, то условия первого критерия продуктивности соблюдены, и матрица есть продуктивной.
. Так как все элементы взятой матрицы неотрицательны, то условия первого критерия продуктивности соблюдены, и матрица есть продуктивной.
Пример
В табл. 10 приведены конечная прямых продукция и коэффициенты затрат отраслей на плановый период (в усл. ден. ед.).
Таблица 10
| Отрасль | Потребление | Конечный продукт | ||
| Промышлен- ность | Сельское хозяйство | |||
| Про- изво- дство | Промышлен- ность | 0,3 | 0,25 | |
| Сельское хозяйство | 0,15 | 0,12 |
Отыскать: 1) плановые количества валовой продукции отраслей, межотраслевые поставки, чистую продукцию; 2) нужный количество валового выпуска каждой отрасли, в случае, если конечное потребление продукции сельского хозяйства увеличится на 20%, а индустрии на 10%.
Тут вектор прямых и 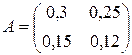 матрица затрат конечной продукции
матрица затрат конечной продукции 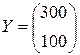 . По формуле вычислим вектор валового выпуска :
. По формуле вычислим вектор валового выпуска : 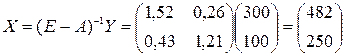 . Отыщем межотраслевые поставки по формулам .
. Отыщем межотраслевые поставки по формулам .
;
;
;
.
Отыщем чистую продукцию отраслей по формуле 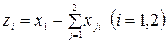 .
.
Тогда ; .
Результаты вычислений сведем в табл. 11.
Таблица 11
| Отрасль | Потребление | Конечный продукт | Валовой продукт | ||
| Произ-водство | Промышлен-ность | 144,6 | 62,5 | ||
| Сельское хозяйство | 72,3 | ||||
| Чистая продукция | 265,1 | 157,5 | |||
| Валовая продукция |
Отыщем новые значения конечного потребления:
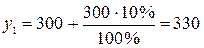 ;
; 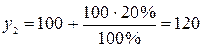 .
.
Новый вектор конечного потребления 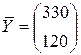 . Отыщем новый вектор валового выпуска
. Отыщем новый вектор валового выпуска 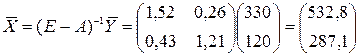 . Так, выпуск в индустрии возможно расширить до 532,8 усл. ден. ед., а в сельском хозяйстве — до 287,1 усл. ден. ед.
. Так, выпуск в индустрии возможно расширить до 532,8 усл. ден. ед., а в сельском хозяйстве — до 287,1 усл. ден. ед.