Дёмина О.Н.
Учебное пособие
Для практических занятий
по дисциплине метрологияпо теме:
ОЦЕНКА ТОЧНОСТИ ГЕОДЕЗИЧЕСКИХ ИЗМЕРЕНИЙ
Брянск, 2013
Неспециализированные положения
Все измерения, как бы шепетильно оно не выполнялись, как бы не был умел наблюдатель, как бы не были современны устройства, сопровождаются неточностями, т.е. отклонениями измеренных значений от подлинных (правильных) значений.
По точности результаты измерений разделяют на равноточные и неравноточные. Под равноточными знают измерения, полученные при измерениях однообразными по точности инструментами, наблюдателями однообразной квалификации, по однообразной методике, в однообразных условиях. В случае, если хотя бы одно из указанных условий не соблюдается, то измерения относят к неравноточным.
Неточности измерений по обстоятельствам их происхождения подразделяются на индивидуальные, инструментальные, неточности окружающей среды. По характеру действия на измеряемую величину неточности измерений подразделяют на неотёсанные, случайные, систематические.
Неотёсанные неточности- это неточности, вызванные промахами либо просчетами наблюдателя, неисправностями устройств, неотёсанным нарушением разработки работ. Для устранения и выявления неотёсанных неточностей нужно делать повторные измерения.
Систематические неточности- это такие Неточности, каковые появляются благодаря определенных обстоятельств и действуют на результаты измерений по определенному закону. Так, при измерении расстояний металлической лентой систематическими являются неточности, вызванные трансформацией длины самой металлической ленты благодаря трансформации температуры. Эти неточности смогут быть устранены из результатов наблюдений методом изучения закона их действия на введения и результаты измерений соответствующих поправок в результаты измерений.
Случайные ошибкивсегда сопутствуют измерениям. Они не смогут был, распознаны из одного измерения, их закономерности проявляются голь ко при производстве массовых измерений. Случайные неточности владеют следующими особенностями:
1. Свойство предела — при определенных условиях
измерений случайные неточности не превосходят наперед заданной величины ( предела).
2. Свойства символа — хорошие и отрицательные случайные неточности появляются в измерениях одинаково довольно часто.
3. Свойство величины — меньшие по полной величине случайные неточности видятся в измерениях чаще, чем громадные.
4. Свойство компенсации — при неограниченно солидном числе измерений предел среднего арифметического из алгебраической суммы случайных неточностей равен:
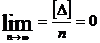
При производстве геодезических измерений (измерений длин, превышений, углов на земной поверхности) появляется необходимость оценить их точность.
ОЦЕНКА ТОЧНОСТИ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
Пускай х},х2,..хп-результаты измерения какой-либо величины.
Опенка точности равноточных измерений производится по следующим формулам и в такой последовательности:
1. Находят возможнейшее (более надежное) значение измеренной величины, им есть среднее арифметическое значение:
Хвер=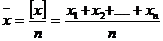 
где — п — число всех измерений.
2Вычисляют отклонения измеренных значений от среднего арифметического (возможнейшего значения) V=хi, — с контролем
3. Вычисляют =V12 + V22 + …..++V2n
4. Вычисляют среднюю квадратичную неточность одного (каждого)
измерения:
m=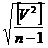 
, (формула Бесселя)
5.Вычисляют среднюю квадратичную неточность возможнейшего значения:
М=
Задача 1.Расстояние измерено металлической лентой пять раз. Результаты измерений приведены в таблице 1. Произвести оценку точности измерений, т.е. вычислить:
1. возможнейшее значение измеренного расстояния;
2. среднюю квадратичную неточность одного измерения;
3. среднюю квадратичную неточность (подлинную и относительную)возможнейшего значения.
| Номер измерений | Результаты измерений, м | Отклонения Vi=хi-хвер,см | V2 |
| 162,28 | -8 | ||
| 162,32 | -4 | ||
| 162,55 | 3+19 | ||
| 162,45 | +9 | ||
| 162,21 | -15 |
Хвер=162,36
Ответ
1. Возможнейшее значение измеренного расстояния:
Хвер =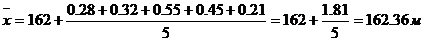 
2. Отклонения измеренных значений от среднегоарифметического (возможнейшего значения):
V1 = 162,28 — 162,36 = — 0,08м = -8см
V2 = 162,32 — 162,36 = — 0,04м = -4см и т.д;
контроль [V] = -8-4+19+9-15 = +1см
3. (V2 ]= 82+42+192+92+152 =747см2
4. Средняя квадратичная неточность одного измерения:
m=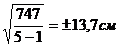 
5. Средняя квадратичная неточность возможнейшего значения:
М=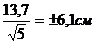 
6. Относительная неточность возможнейшего значения (знаменатель относительной неточности принято округлять до целых сотен):
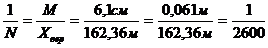
В практике геодезических измерений для исключения и контроля неотёсанных неточностей все измерения делают два раза. Такие измерения именуют двойными. Примером двойных измерений являются измерение углов в теодолитном ходе двумя полуприемами, превышений по чёрной сторонам и красной реек в ходах геометрического нивелирования, длин сторон теодолитного хода в прямом и обратном направлениях и т. д.