ВВЕДЕНИЕ
Расчетно-графические работы выполняются студентами неэлектрических профессий при изучении дисциплины «электроника и Общая электротехника».
Содержание расчетно-графических работ соответствует примерной программе для дисциплины «электроника и Общая электротехника» для высших учебных заведений, рекомендованной Министерством образования РФ 27 февраля 2001 г.
НЕСПЕЦИАЛИЗИРОВАННЫЕ УКАЗАНИЯ ПО Исполнению РАБОТ
И ОФОРМЛЕНИЮ РЕЗУЛЬТАТОВ
Любая расчетно-графическая работа оформляется на стандартных страницах формата А4 (297х210 мм) и должна быть представлена в сброшюрованном виде.
Расчетно-графическая работа обязана содержать:
— титульный лист;
— задание, включающее схему электрической цепи (в случае, если требуется) и данные;
— главную часть, выполненную в соответствии с программой работы и складывающуюся из ответа, нужных рисунков и графических построений;
— перечень использованных источников.
Текст работы разделяется на подразделы и разделы в соответствии с программой работы.
При исполнении работы направляться пользоваться рекомендуемыми учебными пособиями и учебниками, и материалами и конспектом лекций практических занятий по электротехнике.
При оформлении работы на ее страницах нужно выполнять следующие размеры полей: левое – не меньше 20 мм, правое – не меньше 10 мм, верхнее – не меньше 15 мм, нижнее – не меньше 20 мм. Текст работы должен быть четким, разборчивым. Схемы, рисунки и векторные диаграммы должны быть достаточно большими, выполненными с применением чертежных принадлежностей. Векторные диаграммы нужно вычертить на бумаге формата А4 с соблюдением и указанием масштаба.
Расчетно-графическая работа №1
РАСЧЕТ РАЗВЕТВЛЕННОЙ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА
Задание для расчетно-графической работы
Разветвленная цепь синусоидального тока (рис. 1) находится под напряжением , действующее значение которого U = (a+b), В.
Емкостное сопротивление 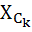 , подключаемое посредством выключателя S, помогает для компенсации реактивной мощности и увеличения коэффициента мощности цепи.
, подключаемое посредством выключателя S, помогает для компенсации реактивной мощности и увеличения коэффициента мощности цепи.
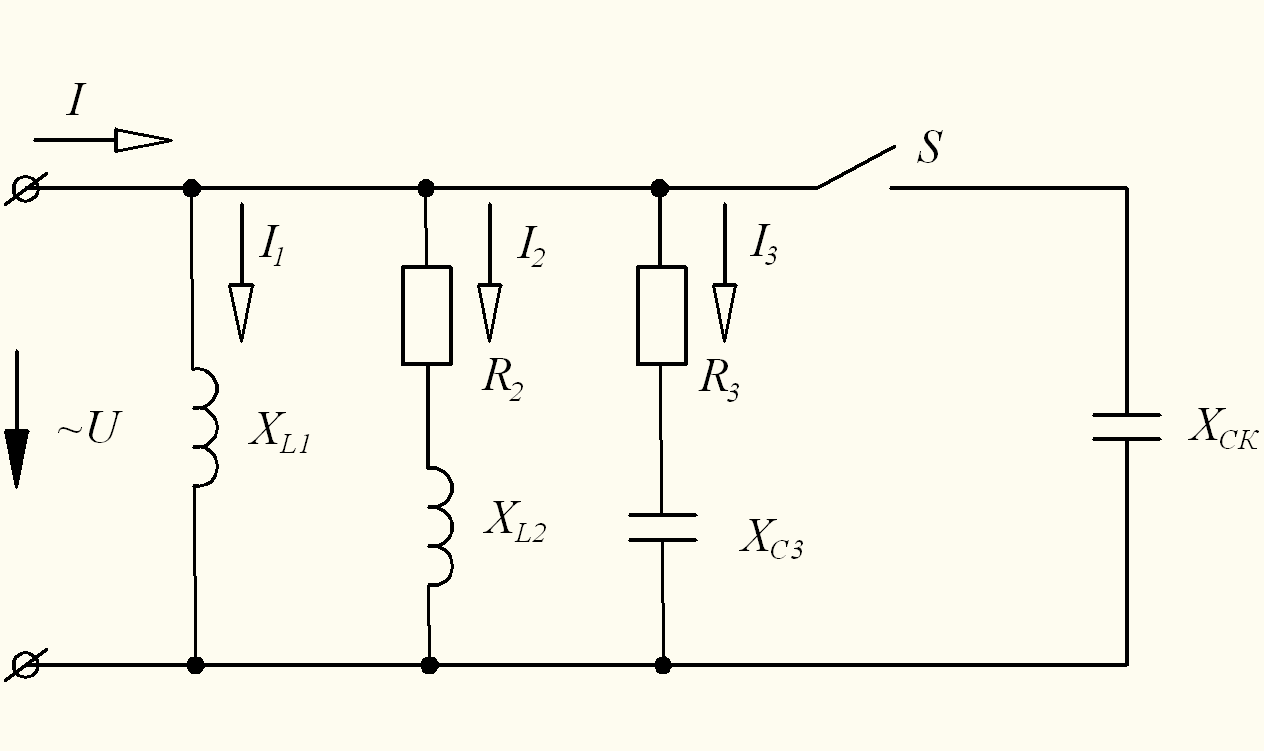
Рисунок 1 – Разветвленная цепь переменного тока
Значения сопротивлений цепи принять:
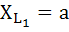 Ом
Ом
Ом
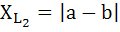 Ом
Ом
Ом
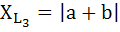 Ом
Ом
Частота: f = 50 Гц.
Значение коэффициента мощности цепи при компенсации реактивной мощности: cos ?’=0,98.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО Исполнению
Пример расчета
Данные:
1. Действующее значение приложенного напряжения U=28 В.
2. Значение сопротивлений цепи:
=19 Ом;
= 9 Ом;
= 10 Ом;
= 19 Ом;
= 28 Ом.
3. Частота f = 50 Гц.
4. Значение коэффициента мощности цепи при компенсации реактивной мощности ‘=0,98.
3.1 Определим токи в ветвях цепи
Определяем полные сопротивления ветвей
Ветвь 1:
=19 Ом.
Ветвь 2: 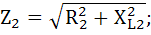
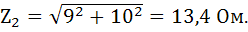
Ветвь 3: 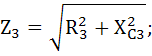
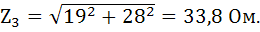
Действующие значения токов в ветвях
Ветвь 1: 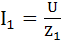 ;
;
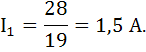
Ветвь 2: 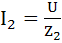 ;
;
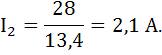
Ветвь 3: 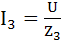 ;
;
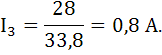
угол сдвига и Коэффициенты мощности по фазе между током каждой ветви и напряжением.
Ветвь 1: 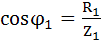 ;
;
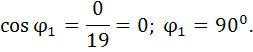
Ветвь 2: 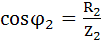 ;
;
Ветвь 3: 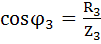 ;
;
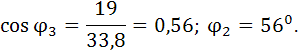
3.2 Определим токи в неразветвленной части цепи
Графический способ
Ток в неразветвленной части цепи на основании первого закона Кирхгофа равен геометрической сумме токов ветвей:
Посредством векторной диаграммы (рис. 2) отыщем действующее значение тока I = 3,09 A.
Аналитический способ
Активные составляющие проводимости ветвей
Ветвь 1: 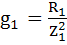 ;
; 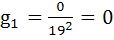 .
.
Ветвь 2: 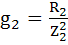 ;
; 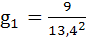 = 0,5 См.
= 0,5 См.
Ветвь 3: 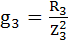 ;
; 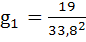 = 0,017 См.
= 0,017 См.
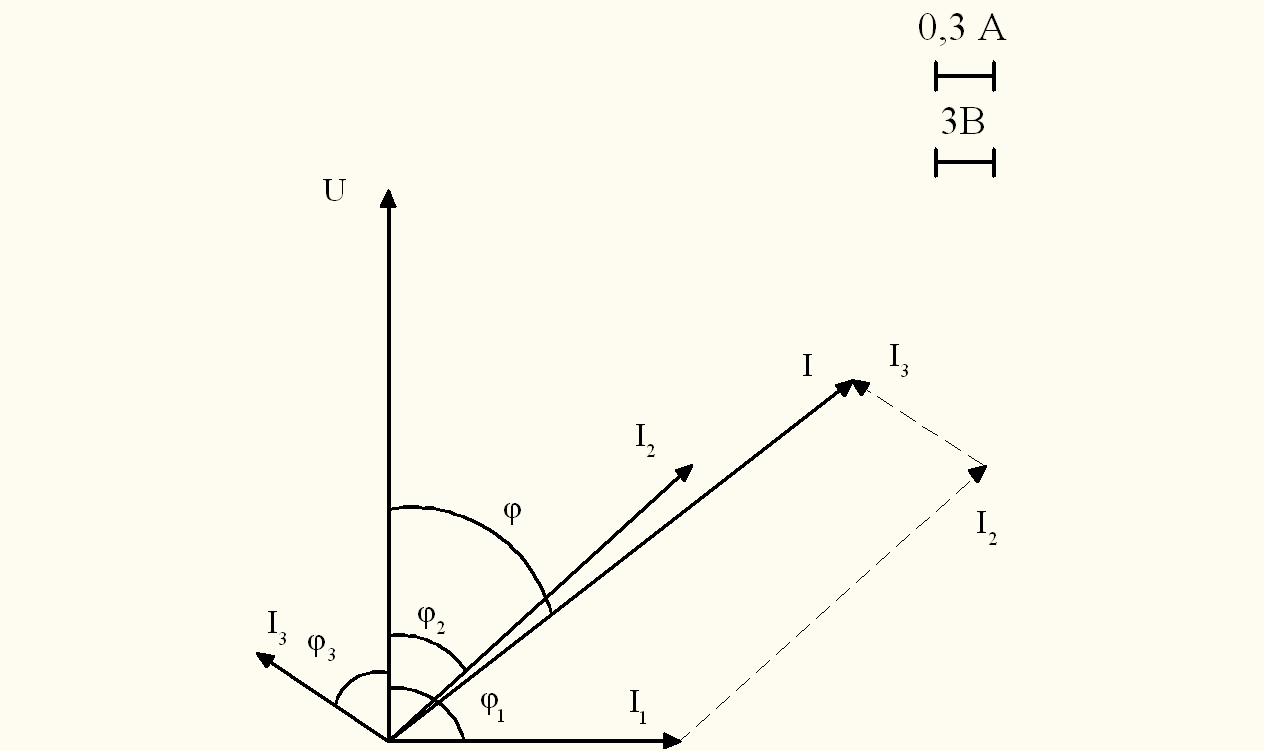
Рисунок 2 — Векторная диаграмма при отключённом тумблер S
Реактивные составляющие проводимости ветвей
Ветвь 1: 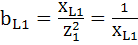 ;
; 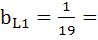 0,053 См.
0,053 См.
Ветвь 2: 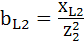 ;
; 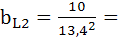 0,056 См.
0,056 См.
Ветвь 1: 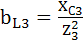 ;
; 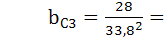 0,024 См.
0,024 См.
Полная проводимость цепи, действующее значение тока в неразветвленной части цепи
Полная проводимость цепи:
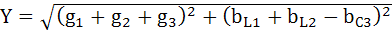 ;
;
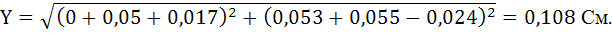
Действующее значение тока:
I=28·0,108=2,02 A.
Вывод: значения тока, полученные графическим и аналитическим методом, совпадают с достаточной точностью.
3.3 Расчет коэффициента мощности, полной, активной
и реактивной мощности цепи
Вычислим коэффициент мощности цепи:
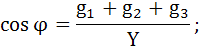
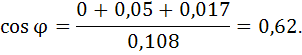
Из этого угол сдвига по фазе между током I и напряжением U:
По векторной диаграмме (рис. 2) угол между напряжением U и током I имеет близкое к расчетному значению:
Полная мощность цепи:
Активная мощность цепи:
Реактивная мощность цепи:
Либо:
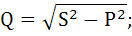
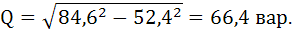
Проверка:
Рассчитываем активную и реактивную мощность каждой ветви.
Ветвь 1: ;
Ветвь 2: ;
Ветвь 1: ;
Суммарная активная мощность цепи:
;
Суммарная реактивная мощность цепи:
;
Вывод: эти полученные на протяжении расчета совпадают с данными взятыми при проверке, следовательно, расчет выполнен, правильно.
3.4 Расчет емкости компенсирующего конденсатора 
Емкость конденсатора СK, подключаемого для компенсации реактивной мощности:
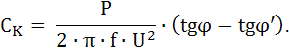
По заданию при компенсации нужно взять коэффициент мощности . Наряду с этим =11,50.
Тогда для заданного варианта:
Емкость конденсатора:
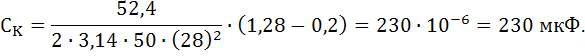
Емкостное сопротивление:
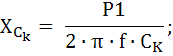

3.5 Расчет тока в неразветвленной части и мощности
цепи при компенсации реактивной мощности
Графический способ
Действующее значение тока в ветви, содержащей 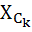 :
:
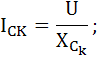
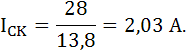
Ток в неразветвленной части цепи определяется векторной суммой:
CK.
Посредством векторной диаграммы (рис. 3) отыщем действующее значение тока:
Угол между напряжением U и током из векторной
диаграммы:
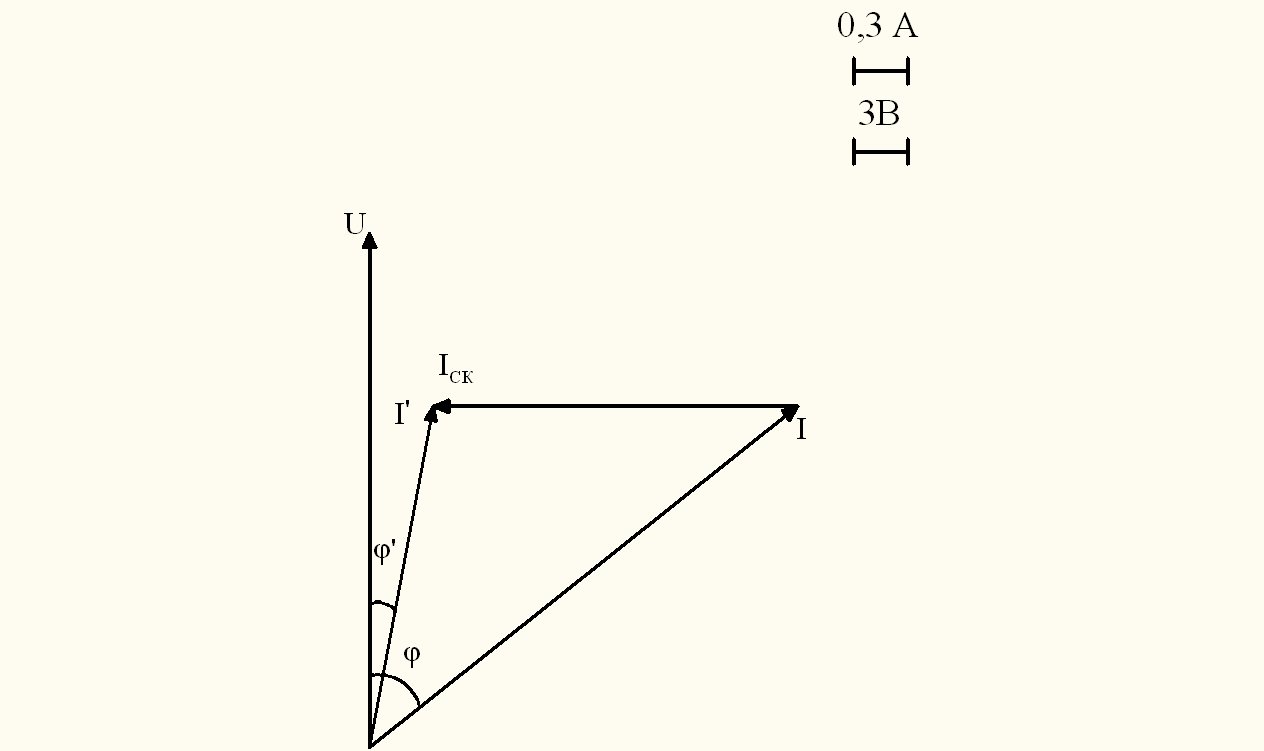
Рисунок 3 — Векторная диаграмма при подключенном тумблер S
(компенсация реактивной мощности)
Аналитический способ
Реактивная проводимость ветви, содержащей 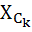 :
:
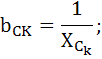
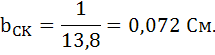
Полная проводимость цепи:
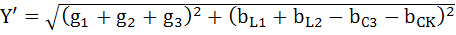 ;
;
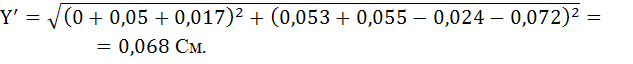
Действующее значение тока:
Определяем полную, активную и реактивную мощности цепи
Полная мощность цепи:
Активная мощность цепи:
Реактивная мощность цепи:
Вывод: компенсация реактивной мощности разрешает существенно уменьшить ток в неразветвленной части цепи и полную мощность цепи при фактически неизменном значении активной мощности.
РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
Задание для расчетно-графической работы
1.1 Трехфазная нагрузка соединена звездой с нулевым проводом (рис. 1) и подключена к источнику с симметричными напряжениями:
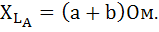
Рисунок 1 — Соединение нагрузки звездой с нулевым проводом
Значение сопротивлений фаз нагрузки выбрать следующим образом.
Для фазы А: 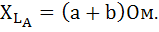
Для фазы В: 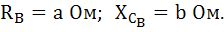
Для фазы С: 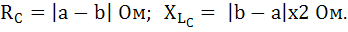
1.2 Трехфазная нагрузка, соединенная треугольником (рис. 2) имеет величину линейного напряжения: .
Значение сопротивлений фаз нагрузки выбрать следующим образом.
Для фазы АB: 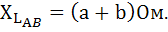
Для фазы ВC: 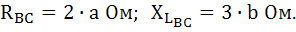
Для фазы СA: 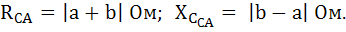
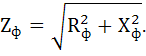
Рисунок 2 – соединение трехфазной нагрузки по схеме соединения «треугольник»
Пример расчета
3.1 Расчет токов, мощностей и напряжений для схемы соединения трехфазной нагрузки звезда с нулевым проводом
Нагрузка соединена по схеме звезда с нулевым проводом представлена на рисунке 1.
Данные:
1. Линейные напряжение UЛ=280 В.
2. Значения сопротивлений цепи:
Фаза А: XLA=28 Ом.
Фаза В: RB=19 Ом; XCB = 9 Ом.
Фаза С: RС=10 Ом; XLC = 20 Ом.
Определяем величину линейных токов IA, IB, Ic. Для этого вычислим полные сопротивления фаз приемника по формуле:
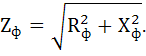
Фаза А:
Фаза В: 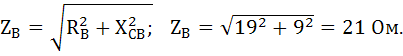
Фаза С: 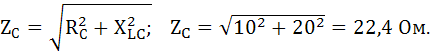
Определим величину фазного напряжения:
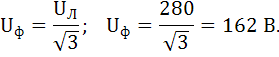
Для заданной схемы соединения нагрузки линейные токи равны фазным:
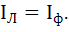
Исходя из этого действующие значения линейных токов рассчитываем следующим образом:
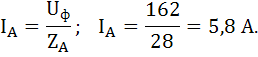
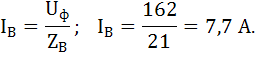
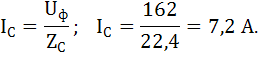
Произведем расчет активной, реактивной и полной мощности цепи. Для этого определим коэффициенты мощности фазы приемника вычислим по формуле:
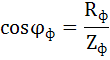
Фаза А: r wsp:rsidR=00000000 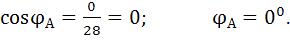
Фаза В: 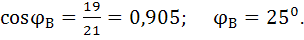
Фаза С: 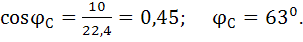
Значение активной мощности нагрузки определяем по формуле:
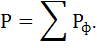
Активная мощность каждой фазы:
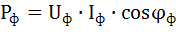 .
.
Для заданной схемы:
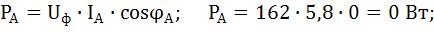
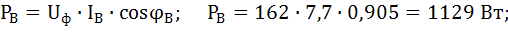
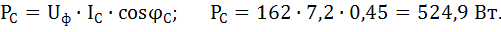
Активная мощность нагрузки:
Значение реактивной мощности нагрузки определяем по формуле:
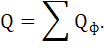
Реактивная мощность каждой фазы равна:
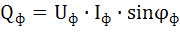 .
.
Для заданной схемы:
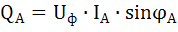 ;
;
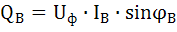 ;
;
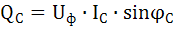 ;
;
Реактивная мощность нагрузки:
Полная мощность нагрузки:
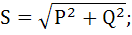
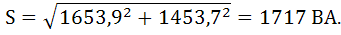
Посредством векторной диаграммы представленной на рисунке 3 определим ток в нулевом проводе. Ток определяем графически на основании векторного уравнения, составленного по первому закону Кирхгофа:
Рисунок 3 – векторная диаграмма токов и напряжений трехфазной нагрузки соединенной по схеме звезда с нулевым проводом
Из векторной диаграммы определяем IN:
3.2 Расчет токов, мощностей и напряжений для схемы соединения трехфазной нагрузки треугольником
Данные:
1. Линейные напряжение UЛ=280 В.
2. Значения сопротивлений цепи:
Фаза АВ: 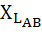 =28 Ом.
=28 Ом.
Фаза ВС: RBС=38 Ом; 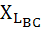 = = 27 Ом.
= = 27 Ом.
Фаза СА: RСА=10 Ом; 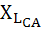 = = 20 Ом.
= = 20 Ом.
Определим величину фазных токов IAВ, IBС, IcА. Для этого определим полные сопротивления фаз приемника:
Фаза АВ: 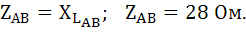
Фаза ВС: 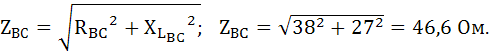
Фаза СА: 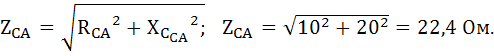
При соединении нагрузки по схеме соединения треугольник фазные напряжения равны линейным напряжениям:
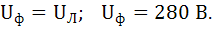
Применяя полученные выше эти, возьмём действующие значения фазных токов приемника:
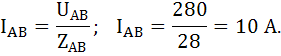
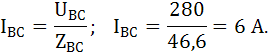
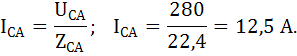
Для определения значений линейных токов выстроим векторную диаграмму. Вычислим углы сдвига между векторами фазных токов и фазных напряжений:
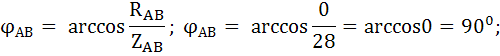
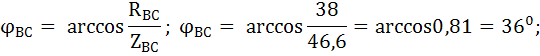
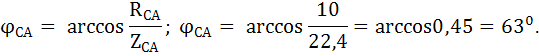
Векторная диаграмма представлена на рисунке 4. Из векторной диаграммы, на основании векторных уравнений, составленных по первому закону Кирхгофа:
определяем значения линейных токов.
Итог:
Значение активной мощности нагрузки определяем по формуле:
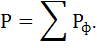
Активная мощность каждой фазы равна:
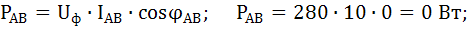
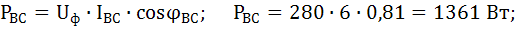
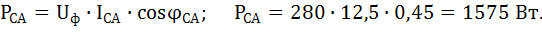
Активная мощность нагрузки:
Реактивная мощность нагрузки определяется по формуле:
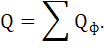
Реактивная мощность каждой фазы:
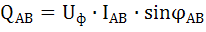 ;
;
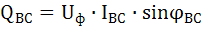 ;
;
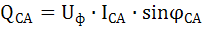 ;
;
Реактивная мощность нагрузки равна:
Полная мощность нагрузки равна:
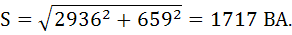
Пример расчета
Трехфазный асинхронный двигатель с короткозамкнутым ротором включен в сеть на номинальное напряжение UH=380 В.
Данные:
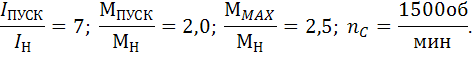
3.1Определение номинального пускового тока электродвигателя
Номинальный ток электродвигателя:
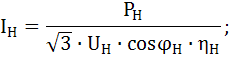
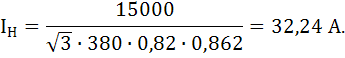
Пусковой ток электродвигателя:
s w:space=720/
3.2 Определение номинального, пускового и большого моментов
Номинальный момент электродвигателя:
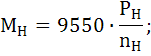
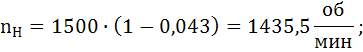
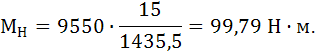
Большой момент электродвигателя:
3.3Расчет мощности потребления двигателем из полных потерь и сети в двигателе при номинальной нагрузке
Мощность, потребляемая двигателем из сети при номинальной нагрузке:
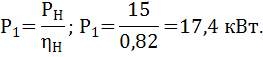
Полные утраты в двигателе при номинальной нагрузке:
3.4 Определение трансформации пускового момента двигателя
при понижении напряжения на его зажимах на 20%
Момент трансформации питающего напряжения на 20 %:
МП.изм.=0,802·МП=0,64·МП=0,64·199,58=127,73
Момент сопротивления рабочей автомобили принимаем равным номинальному моменту электродвигателя:
МС.р.м.= МН=99,79
В итоге: МП.изм. МС.р.м.
Вывод: пусковой момент двигателя при трансформации питающего напряжения на 20 % больше момента сопротивления рабочей автомобили, следовательно, пуск электродвигателя вероятен.
3.5 Построение механических черт двигателя
Расчет значений моментов при разных значениях скольжения производится в соответствии с формулы:
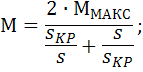
Скорость вращения ротора (вала) определяется по формуле:
Значения скольжения принимаем равными 0; 0,043; 0,1; 0,182; 0,3; 0,5; 0,8; 1,0.
Так, к примеру, для скольжения расчет по этим формулам будет выглядеть следующим образом:
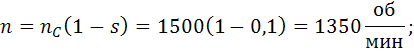
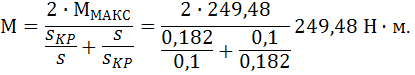
Эти для построения механических черт сведены в таблицу 2.
Таблица 2 — Эти для построения механической характеристики
асинхронного короткозамкнутого двигателя
| s | 0,043 | 0,1 | 0,182 | 0,3 | 0,5 | 0,8 | 1,0 | |
| n, об/мин | 1435,5 | |||||||
| М, Н·м | 111,65 | 210,5 | 249,48 | 221,2 | 160,37 | 107,9 | 87,89 | |
| МИЗМ, Н·м | 71,4 | 134,72 | 159,7 | 141,57 | 102,63 | 56,23 |
Механические характеристики электродвигателя, а также уточненная черта в соответствии с каталожным данным, приведены на рисунке 1.
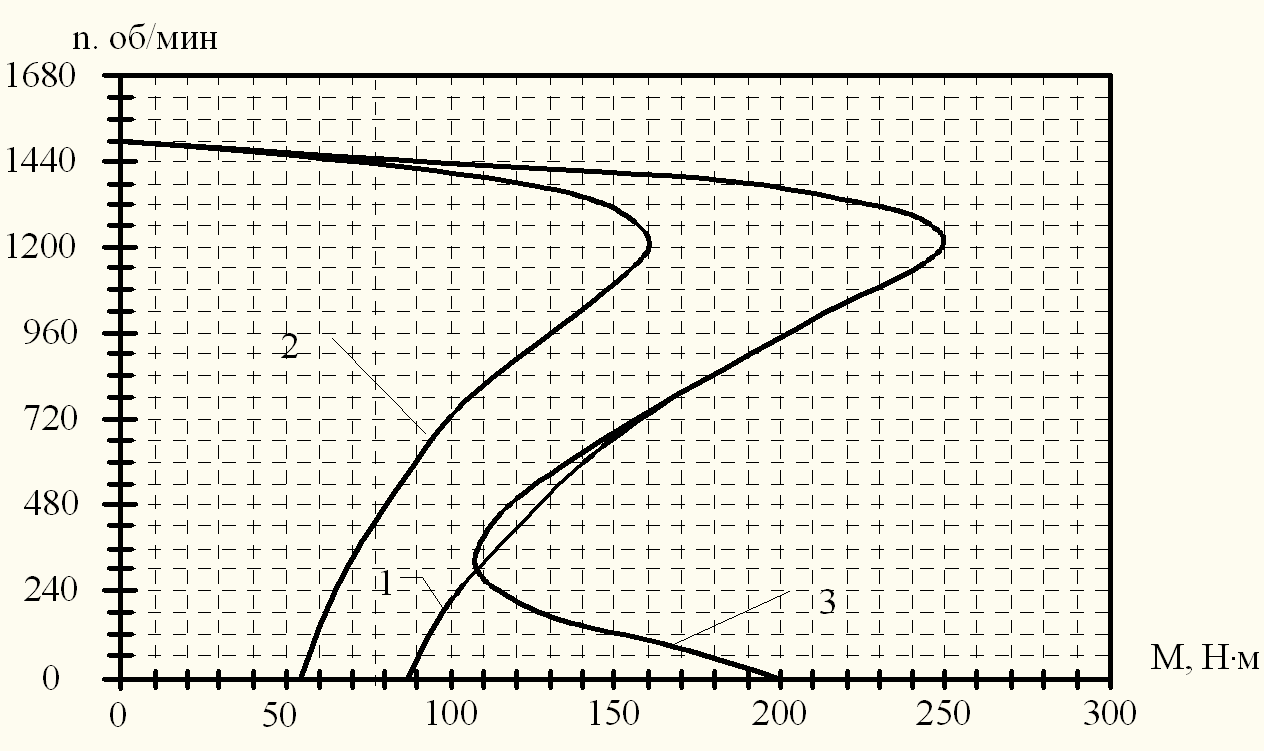
Рисунок 1 — Механические характеристики электродвигателя:
1 – при номинальном питающем напряжении; 2 – при пониженном на 20% питающем напряжении; 3 –черта, откорректированная с учетом каталожных данных.
Вывод:при трансформации питающего напряжения, вращающий момент асинхронного двигателя значительно уменьшается пропорционально квадрату приложенного напряжения. Так как рабочая часть механической характеристики (от 0 до ММАКС) есть твёрдой (небольшой угол наклона фактически линейной зависимости на этом месте), то изменение скорости при уменьшении напряжения будет в маленьком диапазоне.
ЛИТЕРАТУРА
1. Яцкевич В.В. Электротехника. Учебное пособие для с.х. Институтов. МН.: Урожай, 1981.М.40-52 (РГР №1); С.56-64 (РГР №2).
2. Касаткин А.С., Немцов М.Б. Электротехника. – М.: Энерго-атомиздат, 1983. С.80-87, 92 (РГР №1); С.109-120 (РГР №2).
3. Справочник по электрическим автомобилям: В2 т./ Под общ. Ред. И.П. Копылова и Б.К. Клюклва. Т. 1. – М.: Энергоатомиздат, 1988. С.228-230 (РГР №3).
ВВЕДЕНИЕ
Расчетно-графические работы выполняются студентами неэлектрических профессий при изучении дисциплины «электроника и Общая электротехника».
Содержание расчетно-графических работ соответствует примерной программе для дисциплины «электроника и Общая электротехника» для высших учебных заведений, рекомендованной Министерством образования РФ 27 февраля 2001 г.
НЕСПЕЦИАЛИЗИРОВАННЫЕ УКАЗАНИЯ ПО Исполнению РАБОТ
И ОФОРМЛЕНИЮ РЕЗУЛЬТАТОВ
Любая расчетно-графическая работа оформляется на стандартных страницах формата А4 (297х210 мм) и должна быть представлена в сброшюрованном виде.
Расчетно-графическая работа обязана содержать:
— титульный лист;
— задание, включающее схему электрической цепи (в случае, если требуется) и данные;
— главную часть, выполненную в соответствии с программой работы и складывающуюся из ответа, нужных рисунков и графических построений;
— перечень использованных источников.
Текст работы разделяется на подразделы и разделы в соответствии с программой работы.
При исполнении работы направляться пользоваться рекомендуемыми учебными пособиями и учебниками, и материалами и конспектом лекций практических занятий по электротехнике.
При оформлении работы на ее страницах нужно выполнять следующие размеры полей: левое – не меньше 20 мм, правое – не меньше 10 мм, верхнее – не меньше 15 мм, нижнее – не меньше 20 мм. Текст работы должен быть четким, разборчивым. Схемы, рисунки и векторные диаграммы должны быть достаточно большими, выполненными с применением чертежных принадлежностей. Векторные диаграммы нужно вычертить на бумаге формата А4 с соблюдением и указанием масштаба.
Расчетно-графическая работа №1
РАСЧЕТ РАЗВЕТВЛЕННОЙ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА
Задание для расчетно-графической работы
Разветвленная цепь синусоидального тока (рис. 1) находится под напряжением , действующее значение которого U = (a+b), В.
Емкостное сопротивление 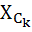 , подключаемое посредством выключателя S, помогает для компенсации реактивной мощности и увеличения коэффициента мощности цепи.
, подключаемое посредством выключателя S, помогает для компенсации реактивной мощности и увеличения коэффициента мощности цепи.

Рисунок 1 – Разветвленная цепь переменного тока
Значения сопротивлений цепи принять:
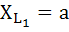 Ом
Ом
Ом
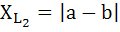 Ом
Ом
Ом
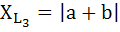 Ом
Ом
Частота: f = 50 Гц.
Значение коэффициента мощности цепи при компенсации реактивной мощности: cos ?’=0,98.