Главные понятия транспортных обслуживающих совокупностей.
Фазы обслуживания. Транспортные обслуживающие совокупности (АТОС) смогут быть однофазовыми и многофазовыми. К примеру, АТОС, в которых прибывшие машины сперва проходят операцию взвешивания, а после этого следуют под погрузку (выгрузку), являются двухфазовыми. В многофазовых совокупностях от фазы к фазе происходит изменение входящего потока.
Каналы обслуживания. Число обслуживающих устройств в фазе: Na , Nb , Nc , … .
Пропускная свойство фазы, канала обслуживания: Va , Vb , Vc , … , где Va=Na*va, Vb=Nb*vb, Vc=Nc*vc, … Тут соответственно va, vb, vc ,… — производительность одного обслуживающего устройства.
Разомкнутые и замкнутые АТОС
В разомкнутых АТОС входящие потоки машин формируются во внешней среде. Они, в большинстве случаев, вероятностен и значительно неравномерны. Разомкнутые АТОС — это, в большинстве случаев, единичные обслуживающие объекты (перевалочный пункт, грузовая автостанция, контейнерный терминал и т.д.).
В замкнутой АТОС машины циркулируют между обслуживающими объектами. Их потоки формируются фазами обслуживания. Автомобиль, попавший в замкнутую АТОС, в большинстве случаев, функционирует лишь в данной совокупности.
Замкнутые АТОС это, в большинстве случаев, сеть обслуживающих объектов.
Режим работы АТОС. В первую очередь, это сменность работы обслуживающих фаз и объектов, окончания рабочих и моменты начала смен (Тн, Тк), длительности рабочих смен (Т = Тк — Тн), составляющих АТОС.
ёмкости и Накопители. Склады, бункеры и т.д. Значения их вместимости Ua,Ub,Uc, … .
Средние значения интенсивностей входящих потоков требований на обслуживание: lт.ср., Qcp., lм.ср. и средние нагрузки на одно требование: qcp., gcp., tм.ср., где:
lт.ср. — интенсивность входящего потока машин, автомоб./сут,
Qcp.- интенсивность прохождения грузов через грузовой пункт, т/сут,
lм.ср. — интенсивность выхода из строя обслуживающих устройств,мех./дни;
qcp. и gcp- соответственно загрузка прибывающего и убывающего машин, г,
t.м.ср. — продолжительность восстановления (ремонта) одного обслуживающего устройства.
Неравномерность поступления требований на обслуживание в обслуживающую совокупность.
Нами рассматривается три вида неравномерностей — внутрисуточная, внутринедельная и сезонная (внутригодичная) — характеризуются собственными конфигурациями. Примеры таких конфигураций приведены на рис. 2.1, 2.3, 2.4.
Рассмотренные выше понятия и их численные значения и другие подобные им являются параметрами совокупности. Понятие параметра совокупности, и понятие черт протекающих в совокупности процессов занимают особенное место в комплексе понятий имитационного моделирования. Их особенная роль обуславливается тем, что они являются составляющими основополагающей формулы ТМО:
M=f(n),
тут свободная переменная, довод — это параметр обслуживающей совокупности, а функция, другими словами простои заявок, ожидающих обслуживания, — черта процессов, протекающих в совокупности.
К чертям обслуживающих процессов относятся не только стоимость и время простоев, но и другие элементы качества работы совокупности. Это, к примеру, общее число груза, перевезенного за единичный отрезок времени, число выполненных за данный же период автомобильных ездок, число необслуженных за рабочую смену машин и т.д.
За единичный отрезок времени в большинстве случаев принимаются дни (время от времени рабочая смена) и, следовательно, характеристики оцениваются собственными средними за сутки значениями.
Чертями АТОС являются:
Мсс — простои транспортных средств в ожидании обслуживания, авт./ч;
Lcc — простои обслуживающих устройств в ожидании работы, мех./ч;
Дсс — задержка (простои) грузов в АТОС, т/ч;
Wcc — количество транспортных средств, оставшихся необслуженными, шт.;
Sсс — количество переработанного груза, т.;
Рсс — количество автомобильных другие показатели и ездок, характеризующие уровень качества работы обслуживающей совокупности.
ВХОДЯЩИЕ ПОТОКИ ТРЕБОВАНИЙ НА ОБСЛУЖИВАНИЕ
НЕСПЕЦИАЛИЗИРОВАННЫЕ СВЕДЕНИЯ О ВХОДЯЩИХ ПОТОКАХ
Входящие потоки (ВП) требований на обслуживание в общем виде относятся к вероятностным процессам. Они исследуются и описываются способами математической статистики и теории вероятностей.
ВП смогут быть потоками единиц транспортных средств (транспортные потоки) и потоками окончания и моментов начала каких-либо событий (в большинстве случаев, моментов выхода из восстановления и строя обслуживающих устройств).
Транспортные ВП — это потоки машин, автопоездов, вагонов, судов, самолетов.
Транспортные ВП характеризуются двумя составляющими: по времени и по величине.
Во времени ВП описываются последовательностью моментов поступления транспортных средств t1, t2, …, ti, …, tN либо последовательностью промежутков между прибывающими транспортными средствами E1=t2-t1, …, Ei=t(i+1)-ti, …, EN=tN-tN-1
По величине ВП описываются последовательностью грузоподъемностей g1, g2, g3, …, gi, …, gN либо размеров груза, прибывающего (убывающего) с одним автомобилем (автопоездом) q1, q2, …, qi, …, qN.
ПОСТРОЕНИЕ ТАБЛИЦ МОДЕЛИРОВАНИЯ ДЕТЕРМИНИРОВАННЫХ СОБЫТИЙ
ПОСТРОЕНИЕ ТАБЛИЦ МОДЕЛИРОВАНИЯ ВЕРОЯТНОСТНЫХ СОБЫТИЙ
К вероятностным событиям на грузовом пункте, обрабатывающем автомобильные грузовые потоки, относятся: количество груза, прибывающего либо убывающего с одним автомобилем, продолжительность диспетчерской обработки автомобиля, продолжительность груза и взвешивания автомобиля, величина промежутка выхода из строя грузового устройства и продолжительность его восстановления и другие. *
Расчет таблицы моделирования соответствующих распределений выполняется на примере распределения количества груза, прибывающего с одним автомобилем (с функцией распределения Fn1(q)). Нужные для расчета значения qi имеются в издании N1.
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА
Значения количества груза qi должны быть сгруппированы. Промежуток группировки определяется по формуле Стерджеса
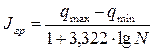
где qmax и qmin — соответственно большое и минимальное значения величины qm,r, N — количество наблюдений (выборки)
В приведенном примере расчета Jrp = 0,82. Результаты расчетов сводятся в таблицу 2.5.
Табл. 4.3
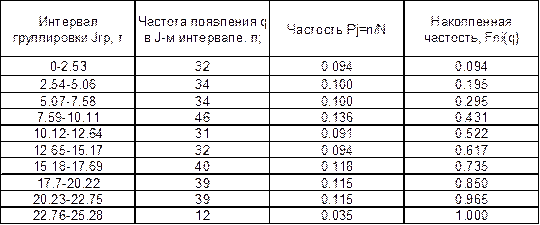
Среднее количество груза, прибывающего с одним автомобилем, определяется по формуле
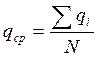=12.06т
Итог расчета по таблице 2.5 — накопленная частость Fnl(q) есть интегральной функцией распределения количества груза, прибывающего с автомобилем.
Строится график функции Fn1(q), как это продемонстрировано на рис. 2.13.
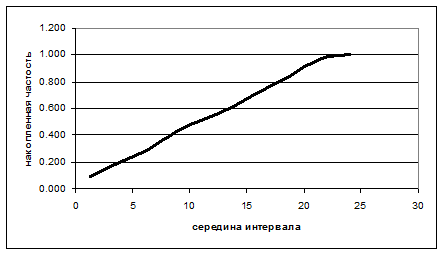
Строится таблица моделирования, как это продемонстрировано в табл. 2.11, при помощи трансформации 10 равномерно распределенных чисел от 1 до 10 через кривую Fn1(q).
Для удобства проведения изменения наложим на график экспоненциальную кривую, соответствующей выстроенной нами как продемонстрировано на рис 2.11.
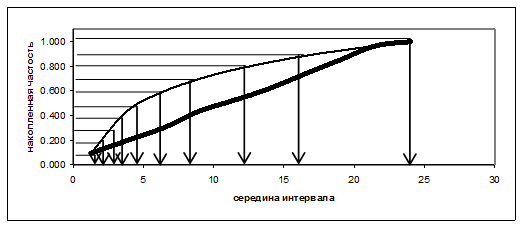
Табл. 4.4.
Таблица моделирования автомобильного потока
| n | значение |
| 1,26 | |
| 1,75 | |
| 2,43 | |
| 3,37 | |
| 4,68 | |
| 6,49 | |
| 9,00 | |
| 12,48 | |
| 17,32 | |
| 24,02 |
Подобным образом рассчитывается таблица моделирования распределения количества груза, убывающего с одним автомобилем Fn2(g).
Расчет таблиц моделирования распределения промежутков между последовательными выходами из строя грузовых длительностей и механизмов их восстановления (соответственно Fn4(Jr) и Fn4(tr)).
Исходный материал для расчетов получается методом проведения натурных наблюдений (хронометража) либо выборки из учетных документов.
Формируются моменты выхода из строя механизмов tr1,tr2,…, и длительности их простоя в ремонте либо техобслуживании tr1, tг2 ,…
Промежуток группировки определяется по формуле Стерджесса, в которой значения qmax и qmin заменяются на значения Jrmax и Jrmin либо на trmax и trmin (соответственно большой и минимальный промежуток между последовательными выходами из строя грузовых механизмов и большая и минимальная длительности их восстановления). Предстоящие расчеты ведутся так же, как в прошлом пункте.
Однако здесь допустим и следующий подход. Распределение промежутков между последовательными выходами из строя грузовых механизмов подчинено закону Пуассона, а распределение длительностей восстановления — обычному закону. В конечном итоге это не всегда так. Последнее не имеет принципиального значения, потому, что главное влияние на процессы, протекающие в грузовом пункте, оказывают не виды распределений, а средние значения этих размеров. В нашем случае
; 
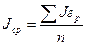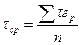
Зная эти значения и применяя графики теоретических функций F1(Jrm) и F2(trm), рассчитываются таблицы моделирования (табл. 2.13 — 2.14).
Табл. 4.5.
Работа крана
| n | значение |
| 0,91 | |
| 1,24 | |
| 1,70 | |
| 2,33 | |
| 3,20 | |
| 4,38 | |
| 6,00 | |
| 8,22 | |
| 11,26 | |
| 15,43 |
Табл. 4.6.
Время восстановления
| n | значение |
| 0,89 | |
| 1,21 | |
| 1,66 | |
| 2,28 | |
| 3,12 | |
| 4,28 | |
| 5,86 | |
| 8,03 | |
| 11,01 | |
| 15,08 |
Рис. 4.6. Окно ввода данных
По окончании чего в главном окне программы нужно ввести время работы грузового двора (с 8 до 18), время работы автотранспорта (с 7 до 22) и мощности грузопотоков А и Б (рис 4.7)
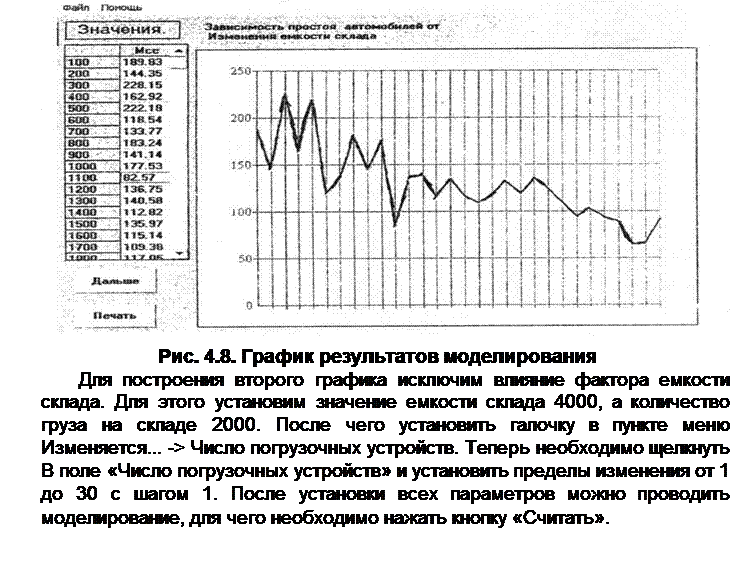
Для построения первого графика нужно установить такое число погрузочных устройств, при котором их влияние на форму графика минимально (в большинстве случаев количество погрузочных устройств должно быть в районе 20). По окончании чего установить галочку в пункте меню Изменяется… — Емкость склада. Сейчас нужно щелкнуть В поле «Емкость склада» и установить пределы трансформации емкости от 100 до 3000 с шагом 100. По окончании установки всех параметров возможно проводить моделирование, для чего нужно надавить кнопку «Вычислять».
В следствии моделирования программа выстроит график зависимости времени простоя автотранспорта (Мсс) от емкости склада (рис 4.8)
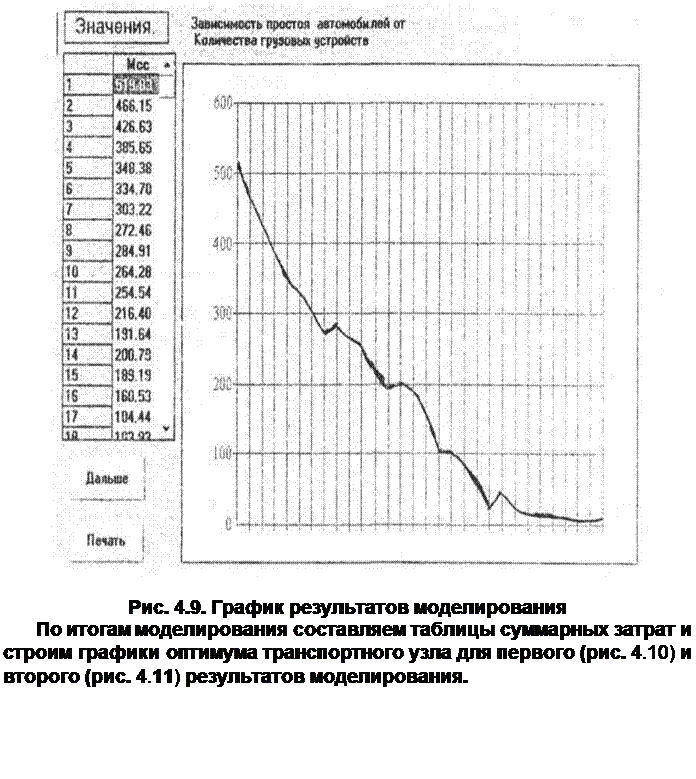
В следствии моделирования программа выстроит график зависимости времени простоя автотранспорта (Мсс) от количества погрузочных устройств (рис. 4.9).
| Емкость склада, гр-т | Цена 1 грузоместа | Суммарные затраты на содержание склада, руб./сут. | Ср. сут. простои автомоб. в ожидании груз, операций, ч | Цена 1 а/ч, руб | Суммарные затраты на простои машин, руб./сут. | Суммарные средние за сутки затраты, руб. |
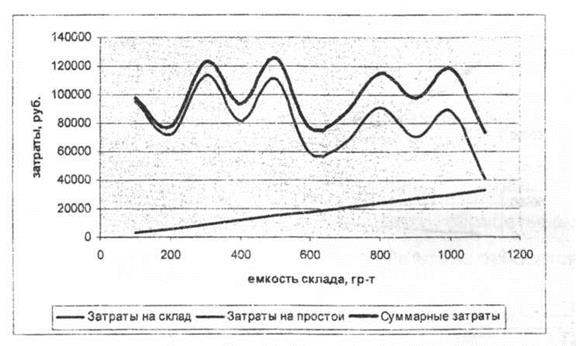
| Рис. 4.10. График зависимости затрат от емкости склада | ||||||
| Кол-во обсл. устр-в | Цена 1ч простоя гр. устр-ва, руб. | Суммарные затраты на простои обсл. устр-в, руб./сут. | Ср. сут. простои автомоб. ожидании груз, операций, ч | Цена 1 а/ч, руб | Суммарные затраты на простои машин, руб./сут. | Суммарные средние за сутки затраты, руб |
| 1930С0 | ||||||
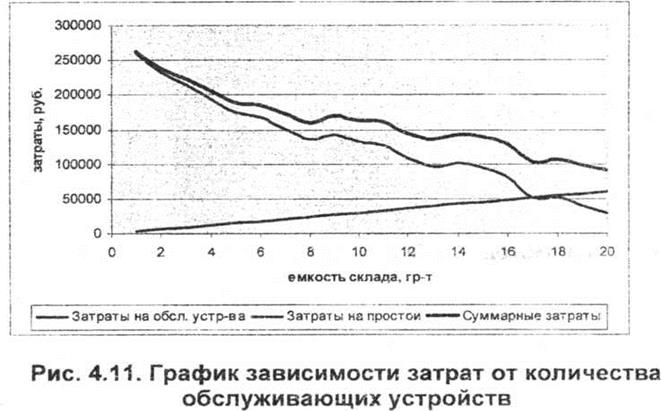
Рис. 5.4. Внутринедельная неравномерность (поток Б)
Для определения сезонных колебаний грузовых потоков употребляются отчетные эти, имеющиеся на грузовом дворе перевалочного пункта либо на автопредприятии. Раздельно учитывается груз, поступивший с автотранспорта, на железную дорогу и с железной дороги на автотранспорт. Отчетные эти, в большинстве случаев, берутся за прошедший год.
Значения относительных размеров месячных грузовых потоков, другими словами потоков грузов, поступающих с машинами на перевалочный пункт, L1, …, L12 определяются по формуле:
,
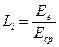где
Ее — количество груза, прибывшего с машинами на ГД в е-й месяц.
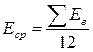, e=1..12
SL=12,000
Для значений Le строится таблица моделирования. Подобно строятся таблицы моделирования для противоположного автомобильного потока — потока грузов, убывающих с машинами с ГД перевалочного пункта.
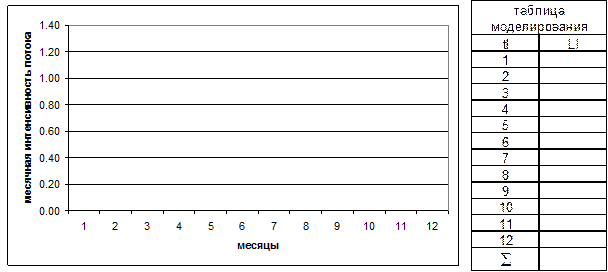
Рис. 5.5. Сезонная неравномерность (поток А)
Рис. 5.6. Сезонная неравномерность (поток Б)
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА
Значения количества груза qi должны быть сгруппированы. Промежуток группировки определяется по формуле Стерджесса
=
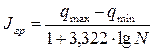где qmax и qmin — соответственно большое и минимальное значения величины qm,r, N — количество наблюдений (выборки)
Результаты расчетов сводятся в таблицу 5.3.
Табл. 5.3
| Промежуток группировки Jrp, т | Частота появления q в J-м промежутке, п; | Частость Pj=n/N | Накопленная частость, Fni(q) |
Среднее количество груза, прибывающего с одним автомобилем, определяется по формуле
=
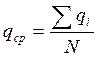Итог расчета по таблице — накопленная частость Fn1(q) есть интегральной функцией распределения количества груза, прибывающего с автомобилем.
Строится график функции Fn1(q), как это продемонстрировано на рис. 5.7.
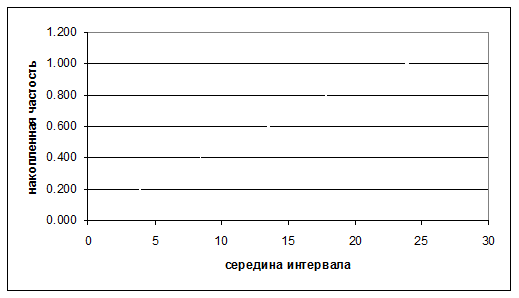
Рис. 5.7. График функции Fn1(q)
Строится таблица моделирования, как это продемонстрировано в табл. 5.4, при помощи трансформации 10 равномерно распределенных чисел от 1 до 10 через кривую Fn1(q).
Для удобства проведения изменения наложим на график экспоненциальную кривую, соответствующей выстроенной нами.
Табл. 5.4.
Таблица моделирования автомобильного потока
| n | значение |
Совершим нужные вычисления для потока порожних машин.
Промежуток группировки определяется по формуле Стерджесса
=
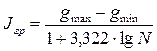где gmax и gmin — соответственно большое и минимальное значения величины gm,r, N — количество наблюдений (выборки)
Результаты расчетов сводятся в таблицу 5.5.
Табл. 5.5
| Промежуток группировки Jrp, т | Частота появления g в J-м промежутке, п; | Частость Pj=n/N | Накопленная частость, Fni(g) |
Среднее количество груза, прибывающего с одним автомобилем, определяется по формуле
=
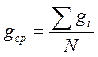Итог расчета по таблице — накопленная частость Fn2(g) есть интегральной функцией распределения количества груза, убывающего с автомобилем.
Строится график функции Fn2(g), как это продемонстрировано на рис. 5.8.
Рис. 5.8. График функции Fn2(g)
Строится таблица моделирования, как это продемонстрировано в табл. 5.6, при помощи трансформации 10 равномерно распределенных чисел от 1 до 10 через кривую Fn2(g).
Для удобства проведения изменения наложим на график экспоненциальную кривую, соответствующей выстроенной нами.
Табл. 5.6.
Таблица моделирования автомобильного потока
| n | значение |
Расчет таблиц моделирования средних промежутков постоянной среднего и работы времени восстановления обслуживающих устройств произведем по той же самой методике.
Выстроим таблицу моделирования среднего времени постоянной работы обслуживающего устройства.
Определим промежуток группировки:
=
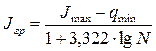Результаты расчетов занесем в табл. 5.7.
Табл. 5.7
| Промежуток группировки Jrp, т | Частота появления в J-м промежутке, п; | Частость Pj=n/N | Накопленная частость, Fni(J) |
Среднее время постоянной работы обслуживающего устройства определяется по формуле:
=
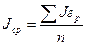Строится график функции Fn3(J), как это продемонстрировано на рис. 5.9.
Рис. 5.9. График функции Fn3(J)
Строится таблица моделирования, как это продемонстрировано в табл. 5.8, при помощи трансформации 10 равномерно распределенных чисел от 1 до 10 через кривую Fn3(J).
Для удобства проведения изменения наложим на график экспоненциальную кривую, соответствующей выстроенной нами.
Табл. 5.8.
Таблица моделирования постоянной работы обслуживающих устройств
| n | значение |
Выстроим таблицу моделирования среднего времени восстановления обслуживающего устройства.
Определим промежуток группировки:
=
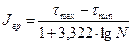Результаты расчетов занесем в табл. 5.9.
Табл. 5.9
| Промежуток группировки Jrp, т | Частота появления в J-м промежутке, п; | Частость Pj=n/N | Накопленная частость, Fni(t) |
Среднее время постоянной работы обслуживающего устройства определяется по формуле:
=
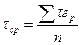Строится график функции Fn4(t), как это продемонстрировано на рис. 5.10.
Рис. 5.10. График функции Fn4(t)
Строится таблица моделирования, как это продемонстрировано в табл. 5.10, при помощи трансформации 10 равномерно распределенных чисел от 1 до 10 через кривую Fn4(t).
Для удобства проведения изменения наложим на график экспоненциальную кривую, соответствующей выстроенной нами.
Табл. 5.10.
Таблица моделирования среднего времени восстановления обслуживающих устройств
| n | значение |
ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Б.П. Безель, Л.Б. Миротин, Т.Б. Сулейменова, Имитация на компьютерах работы транспортно-производственных совокупностей.
2. Л.Б. Миротин, Ы.Э. Ташбаев, Транспортная логистика.
3. Л.Б. Миротин, Транспортная логистика.
4. А. М. Ивахненко, Рынок транспортных одолжений.
5. Н. П. Бусленко, Моделирование сложных совокупностей.
6. Р. Шеннон, Имитационное моделирование совокупностей – наука и искусство.
Главные понятия транспортных обслуживающих совокупностей.
Фазы обслуживания. Транспортные обслуживающие совокупности (АТОС) смогут быть однофазовыми и многофазовыми. К примеру, АТОС, в которых прибывшие машины сперва проходят операцию взвешивания, а после этого следуют под погрузку (выгрузку), являются двухфазовыми. В многофазовых совокупностях от фазы к фазе происходит изменение входящего потока.
Каналы обслуживания. Число обслуживающих устройств в фазе: Na , Nb , Nc , … .
Пропускная свойство фазы, канала обслуживания: Va , Vb , Vc , … , где Va=Na*va, Vb=Nb*vb, Vc=Nc*vc, … Тут соответственно va, vb, vc ,… — производительность одного обслуживающего устройства.
Разомкнутые и замкнутые АТОС
В разомкнутых АТОС входящие потоки машин формируются во внешней среде. Они, в большинстве случаев, вероятностен и значительно неравномерны. Разомкнутые АТОС — это, в большинстве случаев, единичные обслуживающие объекты (перевалочный пункт, грузовая автостанция, контейнерный терминал и т.д.).
В замкнутой АТОС машины циркулируют между обслуживающими объектами. Их потоки формируются фазами обслуживания. Автомобиль, попавший в замкнутую АТОС, в большинстве случаев, функционирует лишь в данной совокупности.
Замкнутые АТОС это, в большинстве случаев, сеть обслуживающих объектов.
Режим работы АТОС. В первую очередь, это сменность работы обслуживающих фаз и объектов, окончания рабочих и моменты начала смен (Тн, Тк), длительности рабочих смен (Т = Тк — Тн), составляющих АТОС.
ёмкости и Накопители. Склады, бункеры и т.д. Значения их вместимости Ua,Ub,Uc, … .
Средние значения интенсивностей входящих потоков требований на обслуживание: lт.ср., Qcp., lм.ср. и средние нагрузки на одно требование: qcp., gcp., tм.ср., где:
lт.ср. — интенсивность входящего потока машин, автомоб./сут,
Qcp.- интенсивность прохождения грузов через грузовой пункт, т/сут,
lм.ср. — интенсивность выхода из строя обслуживающих устройств,мех./дни;
qcp. и gcp- соответственно загрузка прибывающего и убывающего машин, г,
t.м.ср. — продолжительность восстановления (ремонта) одного обслуживающего устройства.
Неравномерность поступления требований на обслуживание в обслуживающую совокупность.
Нами рассматривается три вида неравномерностей — внутрисуточная, внутринедельная и сезонная (внутригодичная) — характеризуются собственными конфигурациями. Примеры таких конфигураций приведены на рис. 2.1, 2.3, 2.4.
Рассмотренные выше понятия и их численные значения и другие подобные им являются параметрами совокупности. Понятие параметра совокупности, и понятие черт протекающих в совокупности процессов занимают особенное место в комплексе понятий имитационного моделирования. Их особенная роль обуславливается тем, что они являются составляющими основополагающей формулы ТМО:
M=f(n),
тут свободная переменная, довод — это параметр обслуживающей совокупности, а функция, другими словами простои заявок, ожидающих обслуживания, — черта процессов, протекающих в совокупности.
К чертям обслуживающих процессов относятся не только стоимость и время простоев, но и другие элементы качества работы совокупности. Это, к примеру, общее число груза, перевезенного за единичный отрезок времени, число выполненных за данный же период автомобильных ездок, число необслуженных за рабочую смену машин и т.д.
За единичный отрезок времени в большинстве случаев принимаются дни (время от времени рабочая смена) и, следовательно, характеристики оцениваются собственными средними за сутки значениями.
Чертями АТОС являются:
Мсс — простои транспортных средств в ожидании обслуживания, авт./ч;
Lcc — простои обслуживающих устройств в ожидании работы, мех./ч;
Дсс — задержка (простои) грузов в АТОС, т/ч;
Wcc — количество транспортных средств, оставшихся необслуженными, шт.;
Sсс — количество переработанного груза, т.;
Рсс — количество автомобильных другие показатели и ездок, характеризующие уровень качества работы обслуживающей совокупности.
ВХОДЯЩИЕ ПОТОКИ ТРЕБОВАНИЙ НА ОБСЛУЖИВАНИЕ
НЕСПЕЦИАЛИЗИРОВАННЫЕ СВЕДЕНИЯ О ВХОДЯЩИХ ПОТОКАХ
Входящие потоки (ВП) требований на обслуживание в общем виде относятся к вероятностным процессам. Они исследуются и описываются способами математической статистики и теории вероятностей.
ВП смогут быть потоками единиц транспортных средств (транспортные потоки) и потоками окончания и моментов начала каких-либо событий (в большинстве случаев, моментов выхода из восстановления и строя обслуживающих устройств).
Транспортные ВП — это потоки машин, автопоездов, вагонов, судов, самолетов.
Транспортные ВП характеризуются двумя составляющими: по времени и по величине.
Во времени ВП описываются последовательностью моментов поступления транспортных средств t1, t2, …, ti, …, tN либо последовательностью промежутков между прибывающими транспортными средствами E1=t2-t1, …, Ei=t(i+1)-ti, …, EN=tN-tN-1
По величине ВП описываются последовательностью грузоподъемностей g1, g2, g3, …, gi, …, gN либо размеров груза, прибывающего (убывающего) с одним автомобилем (автопоездом) q1, q2, …, qi, …, qN.