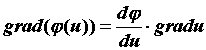И 2-ого рода зависит от того по какому пути он берётся, в случае, если начальнаяи конечная точки однообразные, в случае, если знач. Кр И равны между собой соед. Начальную и конечную точки инт., то говорят,что интеграл не зависит от пути интегрирования.
Теорема 1 Чтобы Кр И по прямой L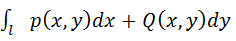 
не зависит от пути интегрирования в некоей области Д нужным и достаточным, дабы он по любому замкнутому контуру Д был равен 0
Необходимость. Интеграл не зависит от пути интегрирования. Доказать.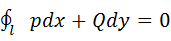 
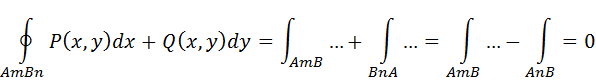
Достаточность. Не зависит от пути интегрирования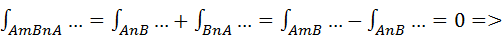 
ПИ-2, определение, вычисление, сообщение с ПИ-1, физический суть
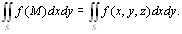
Вычисление ПИ-2сводится к вычислению ДИ по плоской области являющейся проекцией поверхности (символ + в случае, если угол между нормалью и поверхностью острый)
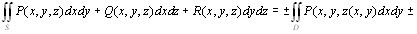
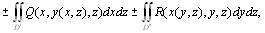
Физический суть поверхностный интеграл 2-го рода является потоком векторного поля через выбранную сторону поверхности S.
Сообщение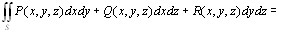 
,
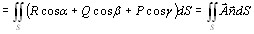И П-1 = И П-2
Формула Стокса
Пускай поверхность S ограничена кусочно-ровным контуром L (рис. 3.14).
Пускай функции: P(x,y,z), Q(x,y,z), R(x,y,z) – непрерывно дифференцируемы на поверхности S.
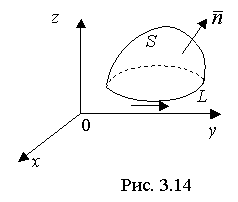
Тогда имеет место формула Стокса:
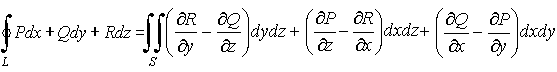
Формула Остроградского-Гаусса
Теорема: В случае, если функции Q(x,y,z); P(x,y,z); R(x;y;z) постоянны совместно со собственными частными производными 1-ого порядка в области V, то имеет место формула:
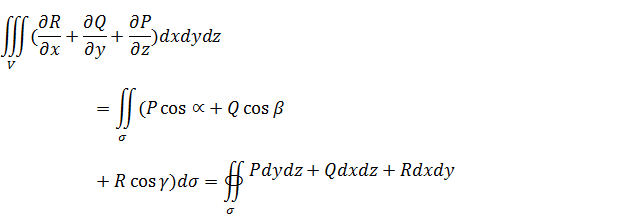
Интегрирование производится по внешней стороне поверхности.
Скалярное поле. поверхности и Линии уровня скалярного поля. Производная по направлению.
Скалярное поле. В случае, если каждой точке пространства ставится в соответствие скалярная величина , то появляется скалярное поле (к примеру, поле температуры, поле электрического потенциала). В случае, если введены декартовы координаты, то обозначают кроме этого
либо . Поле возможно плоским, в случае, если , центральным (сферическим), в случае, если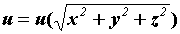 
, цилиндрическим, в случае, если 
.
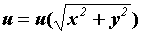линии и Поверхности уровня. Свойства скалярных полей возможно наглядно изучать посредством поверхностей уровня. Это поверхности в пространстве, на которых принимает постоянное значение. Их уравнение: . В плоском скалярном поле линиями уровня именуют кривые, на которых поле принимает постоянное значение: . В отдельных случаях линии уровня смогут вырождаться в точки, а поверхности уровня в кривые и точки.
ПРИМЕР 1. Изучение скалярного поля посредством линий уровня.
Производная по направлению и градиент скалярного поля. Пускай — единичный вектор с координатами , — скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле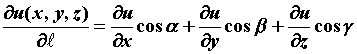 
. Производная по направлению представляет собой скалярное произведение вектора и вектора с координатами 
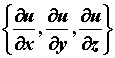, что именуется градиентом функции и обозначается . Потому, что 
, где — угол между и , то вектор показывает направление скорейшего возрастания поля , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно взять следующие особенности градиента:
