И совокупности частиц
В соответствии с основной концепции Ньютона свойства природы в громадных масштабах абсолютно определяются её микроскопическим строением. Исходя из этого изучение природы было бы конечно затевать с нахождения настоящих «установления» характеристик и кирпичиков мироздания, определяющих их движение и состояние. Но свойства настоящих элементарных объектов нам до тех пор пока малоизвестны. В этих условиях, следуя Ньютону, вместо настоящих объектов природы на роль таких «кирпичиков» целесообразно выбирать их идеализированную модель [2].
самая подходящей для этого есть модель частицы, либо корпускулы, интуитивное представление о которой имеет любой человек. Под ней, в большинстве случаев, подразумевается малая часть любого материального объекта. Характерные изюминки данной модели мы начали раскрывать в прошлом семестре (пропедевтический курс физики).
Выделенная роль модели частицы в описании природы определяется двумя событиями. Во-первых, эта модель универсальна, потому что в определённых условиях и настоящая элементарная частица (к примеру, электрон), и пылинка, и биллиардный шар, и планета, и галактика смогут рассматриваться как частицы. Во-вторых, она предельно несложна, потому, что состояние частицы минимально фиксируется всего двумя параметрами, определяющими все остальные её характеристики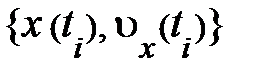 
. Перемещение же частицы, т. е. изменение её состояния со временем, сводится к наглядному процессу перемещения на протяжении траектории 
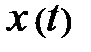(всемирный линии) в пространстве.
До этого момента, например, в работе [3], мы говорили о модели свободной частицы. Но для настоящих обстановок, к рассмотрению которых мы приступаем, частицы испытывает постоянное внешнее действие, но и к ним, однако, применима модель частицы [2]. Это указывает возможность моделирования материальных объектов «несвободными» частицами, характеристики состояния которых изменяются со временем. Такая модель владеет рядом преимуществ. Во-первых, она разрешает применять такую частицу в качестве «зонда» при изучении черт внешних их взаимосвязей и воздействий со особенностями пространства и времени. Во-вторых, в модели «несвободной» частицы узнаваемые характеристики состояния свободной частицы не остаются со временем без трансформации. Поэтому воображает интерес установление объективных черт внешнего действия на частицу, и применение и открытие законов, управляющих трансформацией черт состояния частицы со временем.
Рассуждая о проблемах изучения достаточно несложных совокупностей – или о свободных частицах, или об одиночной частице, испытывающей постоянное действие со стороны окружающих её массивных тел, мы, к тому же, не должны забывать, что в природе значительно чаще видятся совокупности материальных объектов, любой из которых возможно моделировать частицей. Такова, к примеру, Наша система либо рассмотренная ранее нами модель совершенного газа. Неспециализированной изюминкой таких совокупностей есть сотрудничество составляющих их объектов между собой или краткосрочно (к примеру, в газах), или непрерывно (планетные совокупности). Допустимо ли обрисовать подобные совокупности материальных объектов, опираясь на введённые модели свободной и несвободной частицы? Для упрощения аналитического ответа задачи будем разглядывать лишь изолированные совокупности частиц. Одновременно с этим будем помнить, изолированная совокупность взаимодействующих частиц, забранная сама по себе, – это обобщение модели свободной частицы, но только в те моменты, в то время, когда её размерами возможно пренебречь. Так, модель изолированной совокупности взаимодействующих частиц имеет то преимущество, что её свойства жёстко связаны со особенностями пространства и времени, обрисовываемыми основными законами сохранения. Опираясь на эти законы возможно обрисовать перемещение частиц при разных методах их движения и взаимодействия в изолированной совокупности, и перемещение самой совокупности как целого. Наряду с этим у нас появляется возможность постепенного перехода от краткосрочного сотрудничества, проявляющегося в совокупности, к постоянному сотрудничеству, характерному для перемещения совокупности как целого.
Ранее, в работе [3, гл. 4; 5] мы уже применяли процессы краткосрочного сотрудничества частиц, либо, в противном случае, столкновения, для введения последовательности фундаментальных размеров, характеризующих свободную частицу. Переход от свободной частицы к изолированной совокупности частиц, взаимодействующих краткосрочно, разрешил нам сформулировать энергии и сохранения фундаментальные законы импульса для данной совокупности. Выяснилось, знание одних лишь основных законов сохранения разрешает обрисовать многие свойства изолированной совокупности частиц, взаимодействующих краткосрочно, кроме того при отсутствии какой-либо информации о подробностях сотрудничества. Поэтому содержание данной главы сводится к введению характеристик и динамике частиц не только для одиночной частицы, но и для совокупности частиц, определяющих движение и состояние совокупности как целого.
направляться кроме этого обратить внимание на то, что в работе [3, с. 15] нами были предприняты упрочнения по рассмотрению динамики прямолинейного перемещения тел; тут, но, предметом изучения была физическая обстоятельство, обусловливающая тот либо другой темперамент перемещения тела. Но движущееся тело, как мы знаем, складывается из громадного ансамбля частиц, материальных точек – молекул либо атомов. Поэтому конечно появляется вопрос, а «трудятся» ли законы динамики Ньютона при рассмотрении перемещения единичной частицы и каковы предельные размеры разглядываемой частицы? Частично убедиться в этом нам удалось при рассмотрении колебательных процессов, механики целых статистических методов и сред изучения в работе светло синий3, гл. 3; 4; 5].
1.2. Пространственные и временные отношения,
их объективные характеристики
Перед тем как приступить к рассмотрению обозначенных в данной главе вопросов, уместно коротко остановиться на однородности и однородности и изотропности пространства времени; частично эти вопросы были подняты в прошлом семестре [3, с.6–8]. Но к их пониманию на данный момент мы подготовлены лучше, потому, что выработанное сейчас на основании повседневного опыта интуитивное представление о пространстве, времени и перемещении разрешает утверждать: пространство – это порядок обоюдного размещения материальных объектов, высказываемый словами ближе–дальше; время – это порядок сменяющих друг друга состояний материальных объектов, высказываемый словами раньше–позднее. Из этого срочно направляться первое неспециализированное свойство пространства и времени – их относительность. К тому же, сказать о пространстве и о времени без материальных объектов, без каких-то процессов не имеет смысла.
Второе неспециализированное свойство пространства и времени – их взаимозависимость. Не существует пространственных и временных взаимоотношений по отдельности. В природе любой процесс происходит в некоей области пространства, а материальный объект как-то изменяется со временем. Исходя из этого имеет суть сказать только о единых пространственно-временных отношениях между событиями, характеризующими – где и в то время, когда что-то происходит в природе. Каково объективное содержание этих понятий и как их обрисовывать количественно – отечественная цель.
Пространственные и временные отношения относятся к самые фундаментальным понятиям и их нереально свести к вторым, более несложным. В физике такие понятия принято определять путём указания процедуры их измерения. Будем до тех пор пока вычислять, что эти отношения друг от друга не зависят, и дадим их определения, начав с временных взаимоотношений. С целью этого введём эталонный процесс, именуемый часами. В качестве такового возможно применять любой периодический процесс, в котором с достаточной точностью повторяется одно да и то же состояние материального объекта. Примеры аналогичных процессов человечество «поймало» из повседневной судьбы: перемещение Почвы около оси Солнца; пульс человека, колебания математического маятника и т. п. Измерение длительности любого процесса пребывает в его сравнении с длительностью эталонного процесса, играющего роль деления шкалы времени.
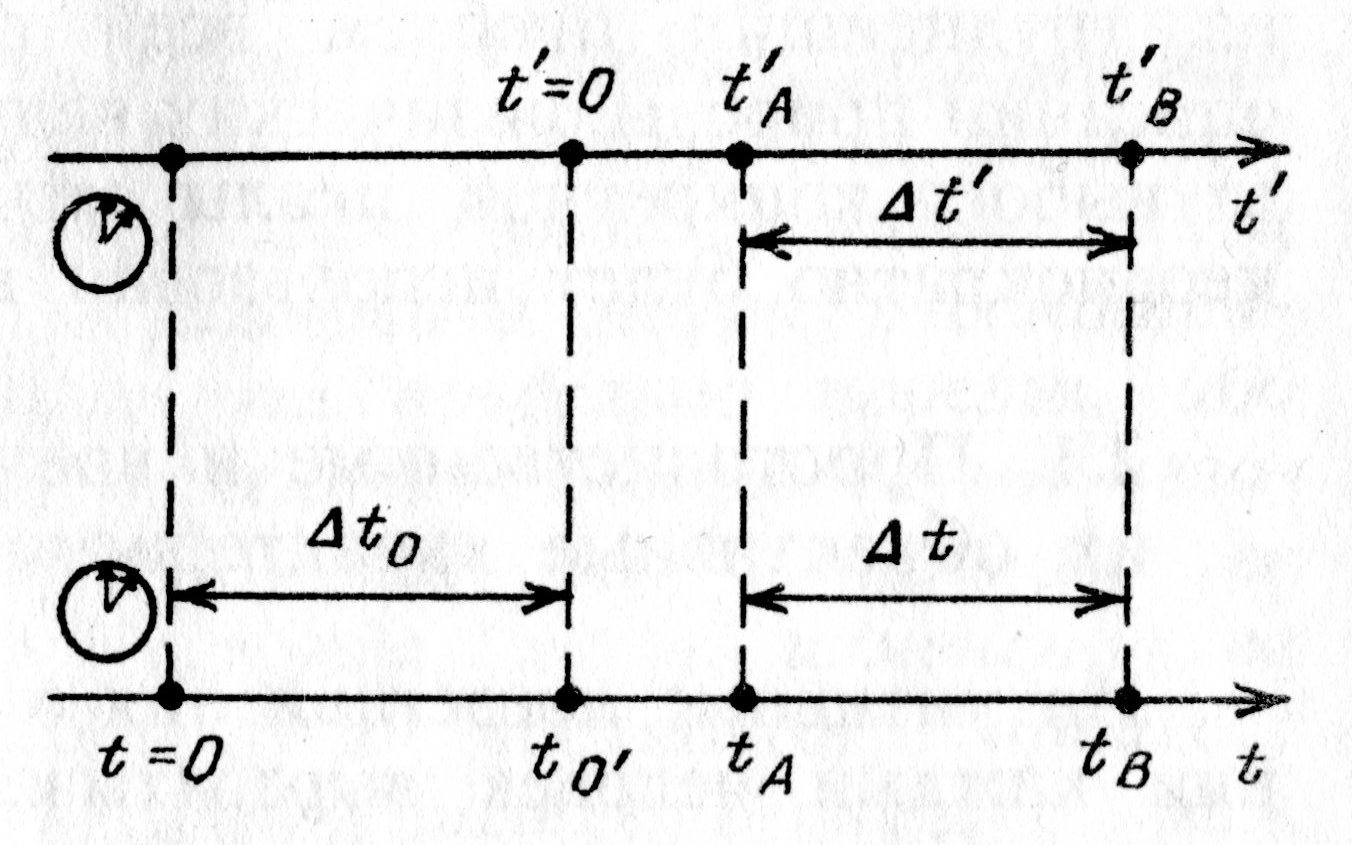 Рис. 1.1. Ось времени и начало её отсчёта |
Для математического описания временных взаимоотношений человечеству было нужно ввести модель настоящего процесса – мгновение. Это процесс, продолжительность которого пренебрежимо мелка в сравнении с длительностью любых вторых процессов в разглядываемой задаче. Разумеется, понятие мгновения довольно (к примеру, год в жизни человека и год в эволюции Почвы). Тогда, приняв произвольное мгновение за начало отсчёта времени любому второму мгновению (к примеру, появлению Вас, читателя, на Земле), возможно поставить в соответствие одно число – момент времени события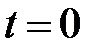 
либо на одномерной шкале – оси времени t временную координату 
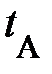(рис. 1.1, нижняя ось времени). Конечно ожидать, моменты времени одного и того же события относительны 
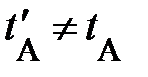(рис.1.1, верхняя ось времени). Они «чувствительны» к выбору начала отсчёта времени, так что сами по себе не являются объективными чертями времени; начало отсчёта верхней оси времени не сходится с началом отсчёта нижней оси времени (рис. 1.1., обратили внимание?). К примеру, в момент Вашего появления читатель в России Ваши дальние родственники в Европе зафиксировали (поставили в соответствие) второе число – момент времени события либо временную координату 
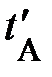на одномерной шкале – оси времени 
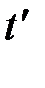; имеете возможность воспользоваться просторами России, проявится то же самое.
Из приведённых выше рассуждений направляться, объективной чёртом временных взаимоотношений может служить только временной отрезок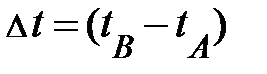 
– это положительное число, владеющее тем свойством, что его значение не зависит от выбора начала отсчёта времени (по какой причине?; проделайте геометрические действия; числовые):
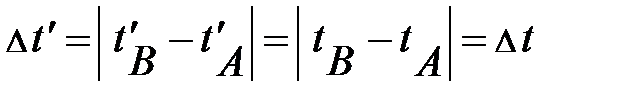. (1.1)
Переходя с символического языка математической записи на знаковый (словесный) язык, возможно сообщить, промежутки времени инвариантны, неизменны по отношению к выбору начала отсчёта времени. В данной аналитической записи, представленной знаковым языком, отражается наиболее значимое свойство времени – его однородность (см. рис. 1.1).
Разобравшись с математическим описанием временных взаимоотношений, перейдём к рассмотрению пространственных взаимоотношений. Очевидно, в обозначенной нами задаче для поступательного перемещения частицы достаточно до тех пор пока выяснить пространственные отношения на протяжении прямой, по которой происходит это перемещение. Для этого нужно ввести эталонный объект, в качестве которого возможно применять любой материальный объект, размер которого фиксирован с достаточной точностью; к примеру, линейка, метр и т.п.
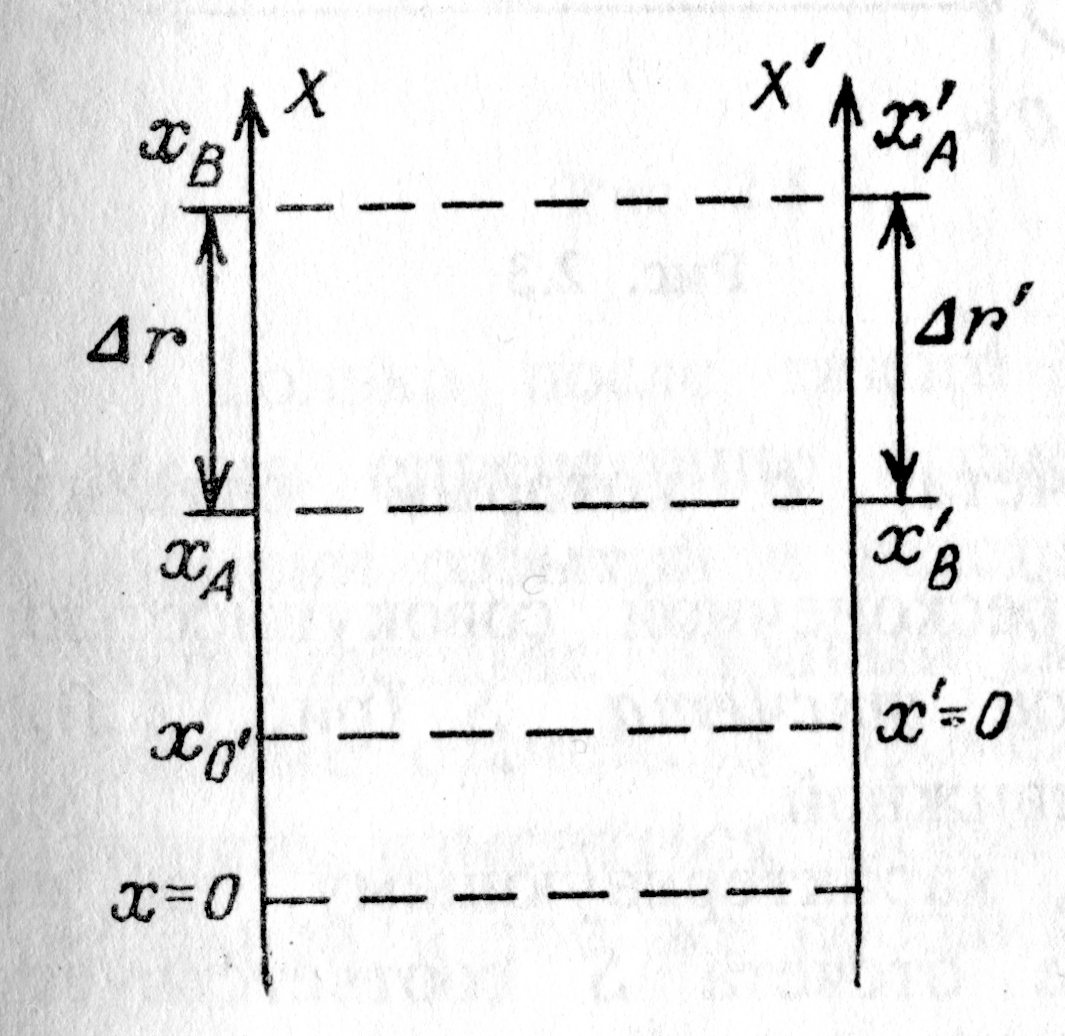 Рис. 1.2. выбор начала и Ось пространства отсчёта |
Для математического описания пространственных взаимоотношений потребуется модель настоящего объекта. Ранее в качестве для того чтобы объекта нами было введено понятие материальной точки либо частицы, корпускулы. В пространственных отношениях предложенная модель играется такую же роль, что и модель мгновения в описании временных взаимоотношений. Вправду, размеры предложенного объекта пренебрежимо мелки в сравнении с расстояниями в разглядываемой задаче. Тогда, приняв произвольную частицу (материальную точку) за пространственное начало отсчёта на протяжении разглядываемой прямой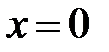 
(рис. 1.2, ось Х слева), каждый материальной точке либо частице на одномерной шкале пространственной оси Х возможно поставить в соответствие одно число – пространственную координату события 
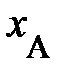, к примеру, появлению вас, читатель, на территории северного района. Разумеется, пространственные координаты одного и того же события А относительны. Они «чувствительны» к выбору начала отсчёта на пространственной оси, к примеру, ось 
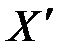(рис. 1.2., справа) 
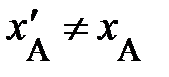; следовательно, сами по себе пространственные координаты не являются объективными чертями пространства. Вправду, событию вашего появления на территории северного района родственниками южного района будет приписана пространственная координата 
.
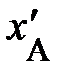Появившиеся трудности смогут быть преодолены, в случае, если мы поступим так же, как это было проделано при математическом описании временных взаимоотношений (1.1). Вправду, в случае, если воспользоваться понятием расстояния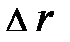 
между двумя частицами (телами) с пространственными координатами в некий момент времени 
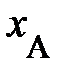и 
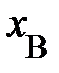, то эта величина не «чувствительна» к выбору начала отсчёта на протяжении пространственной оси. По определению расстояние – это положительное число 
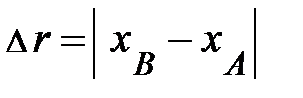и при исполнении математической операции вычитания начало отсчёта, входящее в координаты, уменьшается (убедитесь в этом самостоятельно). Переходя со знакового языка на символический, математическая запись принимает вид:
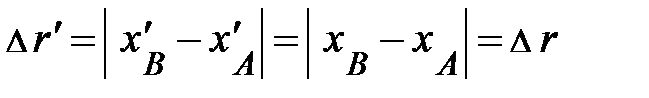. (1.2)
Из данной аналитической записи и рис. 1.2 направляться, значение расстояния 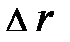не зависит от выбора начала отсчёта на протяжении пространственной оси. Иными словами, расстояния на протяжении оси Х инвариантны, неизменны по отношению к выбору начала отсчёта на пространственной оси. В этом отражается наиболее значимое свойство пространства – его однородность.
1.3. Характеристики прямолинейного перемещения.
Понятие о состоянии частицы и мире событий
Приведённые выше описания временных и пространственных взаимоотношений можно считать свободными только условно. В действительности необходимость анализа поведения материальных объектов в пространстве с течением времени неизбежно ведет к переходу к взаимосвязанным пространственно-временным отношениям. Их математическое описание возможно взять, объединив введённые описания взаимоотношений (рис. 1.1 и 1.2) на протяжении осей х и t соответственно. Для этого мы связывали декартову совокупность координат с телом отсчёта и «местными» часами [3], что разрешило нам ввести понятие совокупности отсчёта. В этом случае каждому событию, характеризующему где и в то время, когда находится частица (тело), в совокупности отсчёта S (рис. 1.3) соответствует мировая точка А либо два числа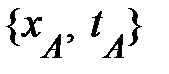 
, каковые совместно играют роль пространственно-временных координат для того чтобы события. Так, от условно-свободного описания пространственных взаимоотношений на протяжении оси Х и временных взаимоотношений на протяжении оси t мы перешли к более соответствующему природе взаимосвязанному описанию пространственно-временных описаний на плоскости Хt, т.е. в двумерном мире событий. Конкретно таковой подход разрешал нам в ранних работах [3] фиксировать временной отрезок 
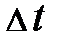между моментами времени событий и расстояние 
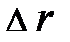между пространственными координатами этих событий.
Вправду, понятия событие, мировая точка, мир событий в повседневной судьбе неявно применяет любой человек. Ранее без них мы не могли обрисовать кроме того столь простое явление, как прямолинейное перемещение. В частности, одного указания на то, что траектория частицы – это прямая, к примеру, ось Х, для описания частицы слишком мало. На протяжении одной и той же прямой частица может двигаться направо либо налево, равномерно либо неравномерно (рис. 1.3) и т. п. Исходя из этого для последовательного описания прямолинейного перемещения нужно применять «двумерный» мир событий. В нём с прямолинейным перемещением частицы на протяжении оси Х сопоставляется постоянная совокупность событий, показывающих, где и в то время, когда находится движущийся объект. По сути на плоскости Хt прямолинейное перемещение изображается постоянной кривой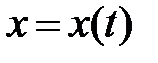 
произвольной формы (рис. 1.3), которую ранее мы именовали графиком перемещения либо всемирный линией. В случае, если движущееся тело покоится, его мировая линия (график перемещения) – прямая, параллельная оси времени: 
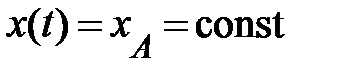(рис.1.3.); при равномерном перемещении мировая линия – наклонная прямая вида: 
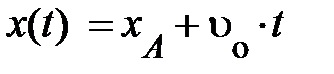(рис. 1.3), скорость 
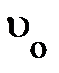возможно как хорошей, так и отрицательной величиной в зависимости от направления перемещения на протяжении оси Х. Очевидно, её значение не зависит от выбора начала отсчёта на протяжении оси Х и начала отсчёта времени. При неравномерном перемещении мировые линии движущегося тела (частицы, материальной точки) имеют вид незамкнутых кривых (рис. 1.3), для которых на любом участке 
.
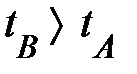Итак, физики, опираясь на математический аппарат (пускай и простой в нашем случае), продемонстрировали, черта быстроты перемещения – скорость – определяется через пространственные и временные отношения, определение которых со своей стороны связано с перемещением [2, 6]. Это показывает, что всякое раздельное рассмотрение пространственных и временных взаимоотношений (кроме того в неподвижной совокупности отсчёта) есть непоследовательным. Окружающая же нас природа существует в едином многообразии – мире событий, в котором понятие пространства, времени и перемещения взаимосвязаны и неразрывны. Говоря тут для простоты о двумерном мире событий – плоскости Хt – мы в действительности имеем дело не с отношениями на протяжении отдельных осей Х и t, а принципиально с отношениями на плоскости Хt. Это целостное двумерное многообразие, на котором заданы как расстояния и промежутки времени, так и каждые мировые точки событий, и мировые линии любой формы, соответствующие перемещению материальных объектов.
Какое отношение имеет сообщённое выше для вопроса, обозначенного в данной главе?
Во-первых, мы убедились в том, что в случае, если задан график перемещения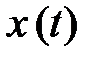 
в мире событий при всех значениях t, прямолинейное перемещение частицы (тела) обрисовано абсолютно. Во-вторых, в случае, если задана мгновенная скорость частицы 
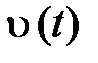при всех значениях t, её график перемещения возможно отыскан с точностью до постоянной 
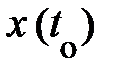. Но в настоящих условиях ни то, ни второе, в большинстве случаев, неизвестно. Замечая поступательное перемещение автомобиля, биллиардного шара, космического корабля мы имеем возможность выяснить с некоей точностью его мгновенную 
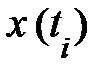скорость и координату 
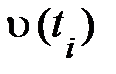в любой момент времени. По сути вместо графика перемещения либо мгновенной скорости при любых значениях времени, мы имеем дело с локальными значениями скоростей 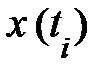и координат 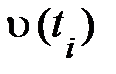. В случае, если учесть, что мировые линии материальных объектов, моделируемых частицами, в любой момент постоянны, то, как показывают математики, знания этих размеров достаточно, дабы угадать их значения в последующие моменты времени 
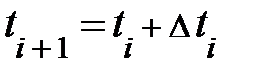. Всё это показывает на то, что при прямолинейном перемещении совокупность двух свободных размеров { 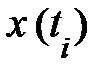, 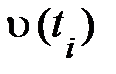} в любую секунду времени определяет как состояние частицы, так и последующее изменение её состояния со временем.
|
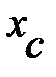
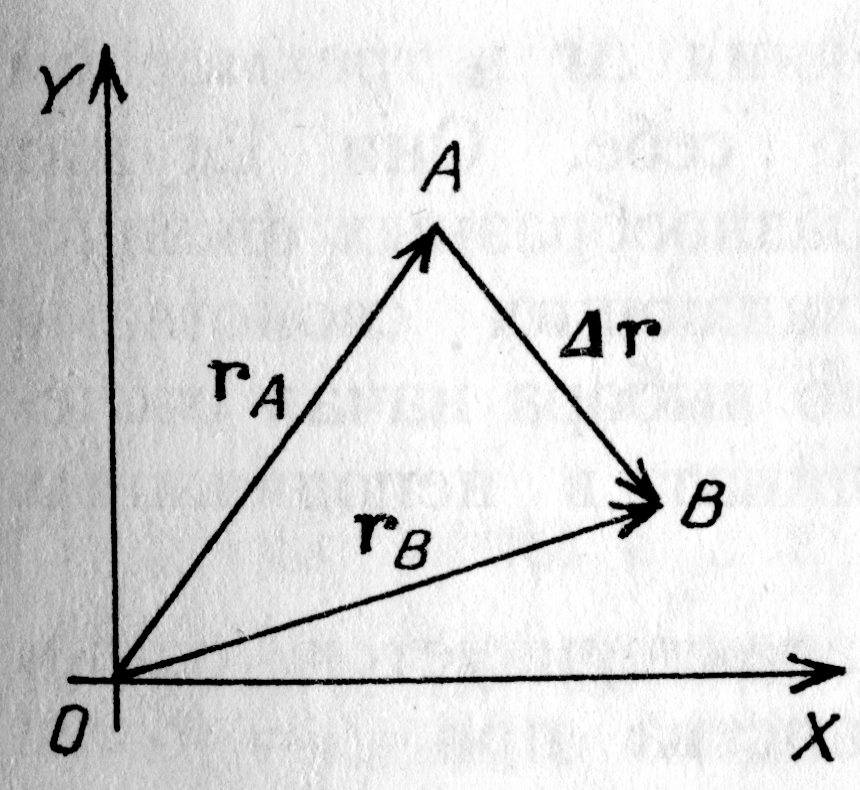 Рис. 1.4. Скалярные и векторные размеры на плоскости |
|
|
|
|
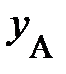
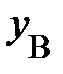
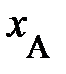
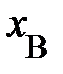
Не менее важно тут обратить внимание на то, что физики предпочитают сопоставлять физические размеры не просто с числами, а со особыми векторами образами – и математическими скалярами. Дело тут, по-видимому, в том, что физиков интересуют объективные законы природы. Объективность возможно обеспечить, в случае, если форма записи законов не «чувствительна» к выбору конкретной совокупности отсчёта, т.е. есть ковариантной, неизменной. Для неподвижных совокупностей отсчёта этого возможно добиться, в случае, если физические законы записывать через векторы и скаляры. (По какой причине?) Скалярная физическая величина расстояние 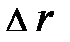характеризуется одним числом и имеет в данной точке пространства однообразное значение в любой неподвижной совокупности отсчёта. Векторная физическая величина – вектор расстояния 
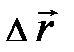характеризуется направлением и численным значением в пространстве. Вектор расстояния 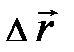(рис. 1.4) – пример математической величины, владеющей не только численным значением, но и направлением. Графически вектор принято изображать стрелкой, направленной от А к В, а его модуль в двумерном пространстве (для простоты записи) возможно представлен через проекции на координатные оси следующим образом: 
.
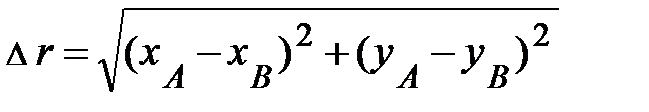Необходимо заметить, запись физических законов (в неподвижных совокупностях отсчёта) через векторы и скаляры значительна только для установления самих этих законов либо для демонстрации каких-то неспециализированных объективных особенностей. Для практических же целей их целесообразно спроецировать на оси более эргономичной неподвижной совокупности отсчёта; этим мы, кстати, и занимаемся при ответе задач.
Так, изотропности пространства и свойства однородности, разрешившие выделить объективные характеристики пространственных взаимоотношений, предопределяют самые общие особенности любых физических размеров, пригодных для объективного описания природы. Вместе с этим законы, записанные в форме математического соотношения, содержащего векторы и скаляры, ковариантны, т е. имеет однообразный вид в любой неподвижной совокупности отсчёта.
1.4. Принцип инерции. Импульс как черта
состояния частицы
Обсуждение пространственно-временных взаимоотношений разрешило прописать поступательное перемещение частиц (корпускул) и распознать наиболее значимые характеристики состояния материального объекта { 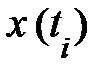, 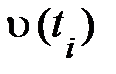}. Эти понятия имели суть объективных черт, потому что они не зависели от выбора конкретной неподвижной совокупности отсчёта (рис. 1.2.). Одновременно с этим настоящие тела отсчёта смогут двигаться. Исходя из этого заблаговременно нельзя утверждать, что их перемещение не оказывает влияния на форму физических законов в связанных с ними совокупностях отчёта и выбор самих объективных черт, благодаря которым следовало бы формулировать эти законы. Дабы отделить влияние конкретного выбора движущейся совокупности отсчёта от объективного содержания законов природы, нужно было бы сравнить формы каждого для того чтобы закона в разных движущихся совокупностях отсчёта. Но для этого нужно заблаговременно установить объективные законы, обрисовывающие перемещения самих материальных объектов, служащих телами отсчёта. Физики нашли выход из этого логически замкнутого круга (к примеру, см. [2]). В качестве «пробного камня» выбирают, во-первых, самый несложный закон природы и, во-вторых, таковой закон, что возможно было бы применять для описания перемещения совокупностей отсчёта. Несложным типом перемещения тел отсчёта, как мы знаем, есть поступательное, моделируемое перемещением одной частицы. Конечно, изучение перемещения частицы разрешает установить и темперамент влияния перемещения тел отсчёта на форму законов природы.
Из опыта известно, темперамент перемещения частицы зависит от действия на неё окружающих материальных объектов, причём с удалением частицы от них это действие убывает. Сейчас представим идеализированную обстановку – частица движется столь удалённо от всех остальных материальных объектов (включая и тело отсчёта), что их действием на неё возможно по большому счету пренебречь. Кстати, такую частицу принято именовать свободной. В настоящих условиях примером перемещения свободной частицы может служить установившееся перемещение парашютиста; тяготение Почвы компенсируется сопротивлением воздуха.
Разумно предположить, в мире событий (§ 1.3) график перемещения свободной частицы х =х(t) должен быть максимально несложен. Изучая форму мировых линий на плоскости Хt(рис. 1.3), нетрудно осознать – несложной формой владеют мировые линии, для которых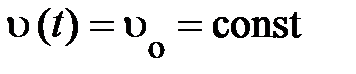 
, включая и 
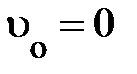(см. рис. 1.3). Из этого срочно направляться, несложным типом перемещения частицы есть прямолинейное равномерное перемещение и конкретно так обязана двигаться свободная частица в некоторых совокупностях отсчёта.
Закон перемещения свободной частицы (принцип инерции) был сформулирован ещё в начале XVII в. Г. Галилеем. В современной трактовке, как первый закон Ньютона, принцип инерции читается так: существуют совокупности отсчёта, в которых каждая свободная частица движется равномерно и прямолинейно либо покоится. Очевидна его тесная сообщение с проблемой выбора совокупностей отсчёта, довольно которых должна быть инвариантна (неизменна) форма законов природы, исходя из этого он был первым основным законом физики. Совокупности отсчёта, в которых выполняется закон инерции, именуются инерциальными; все остальные – неинерциальными.
Тут уместно подметить, не обращая внимания на внешнюю простоту принципа инерции, это одно из наибольших достижений в истории физики; с этого момента стало возмможно формулировать объективные законы природы, а физика появилась как наука.
Из закона инерции направляться серьёзный вывод, скорость – это черта перемещения свободной частицы. При наличии же внешнего действия это уже не так – различные частицы, двигавшиеся первоначально с однообразной скоростью, изменяют её по-различному. Это значит, кроме скорости частицам (телам) свойственна какая-то черта, отличающая одну частицу от второй и играющая роль внутренней характеристики самой материи. Таковой универсальной чёртом материи помогает масса. В области привычных для нас скоростей имеет место правило – в одних и тех же условиях более массивное тело способно купить меньшую скорость; т. е. оно более инертно. Понятие массы m(инертной) столь же
| Рис. 1.5. Распад объекта, к которому применима модель частицы |
привычно, как и понятие пространства и времени. Оно не сводится к более несложным понятиям, исходя из этого массу возможно выяснить лишь через измерение. Как именно? Пускай у нас имеется материальный объект, к которому применима модель свободной частицы; для простоты будем вычислять, что объект первоначально покоится. Примерами таких обстановок могут служить два грузика соединённые пружинкой; орудие, складывающееся из снаряда и лафета; радиоактивный атом. Предположим, что из-за внутренних сотрудничеств через некий временной отрезок объект распадается на два объекта (рис. 1.5), к каждому из которых применима модель частицы. Удаляющиеся друг от друга частицы 1 и 2 можно считать свободными. Опыты для того чтобы рода свидетельствуют, между скоростями двух частиц по окончании распада существует определённая сообщение. В частности, в случае, если исходная частица до распада покоилась,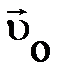 
=0 (представлено пунктиром), то частицы 1 и 2 движутся на протяжении прямой, а векторы 
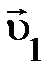и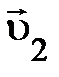 
направлены в противоположные стороны (рис. 1.5.). Моделируя распады
|
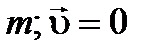
одной и той же исходной частицы, возможно найти, значения каждого модуля скорост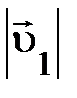и 
и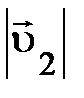 
смогут изменяться, но их отношение не зависит от самих 
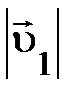и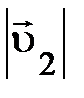 
, оставаясь постоянным: 
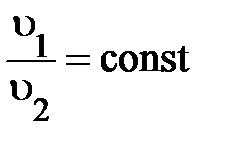. Помимо этого, в случае, если исходная частица распалась на две другие частицы, то это отношение измениться, но снова 
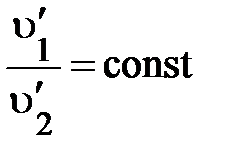. Разумеется, отношение модулей скоростей появившихся частиц характеризует какое-то их внутреннее свойство не связанное конкретно с перемещением. Всё это показывает на то, что отношение модулей скоростей частиц, образующихся при распаде покоящейся исходной частицы, обратно пропорционально их весам, характеризующим свойство изменять собственную скорость в одних и тех же условиях. Аналитически это возможно представлено так:
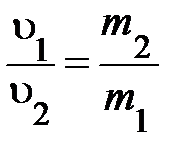. (1.3)
Не обращая внимания на простоту, утверждение (1.3) не противоречит интуитивным представлениям об инертности – из двух частиц, появившихся при распаде, меньшей скоростью (по модулю) владеет частица с большей массой. Оно так же даёт метод измерения инертной массы, к примеру, на борту космического корабля. На практике используются другие способы (какие конкретно?).
Так, масса есть «визиткой» частицы – к примеру, элементарной, из которой состоят атомы, молекулы и более большие тела. Из опыта направляться, где бы и в то время, когда бы ни была обнаружена подобная частица, её масса остаётся одним и тем же внутренне свойственным ей числом. Оно не «чувствительно» к положению частицы в пространстве и к моменту времени её наблюдения. Всё это разрешает предположить, масса – скалярная величина, не зависящая от выбора инерциальной совокупности отсчёта, а повседневный опыт подсказывает, она владеет свойством аддитивности (складывающиеся):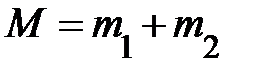 
. Это свойство массы в повседневном опыте укладывается в интуитивное представление о том, что масса макроскопического тела пропорциональна его количеству.
Тут мы подошли к серьёзному выводу – для всестороннего описания перемещения свободной частицы нужно знать не только её скорость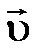 
, но и массу 
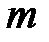. Конкретно исходя из этого Ньютон, в первый раз, и внес предложение применять в качестве комплексной характеристики перемещения частицы векторную величину импульс: 
.
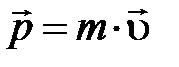В его важности возможно убедиться, воспользовавшись двухчастичным распадом (рис. 1.5). Потому, что по окончании распада частицы постоянно разлетаются по прямой в противоположные стороны, из формулы 1.3 приобретаем: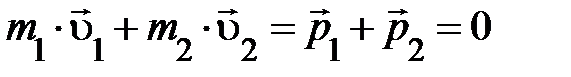 
. В это же время, до распада частица покоилась ( 
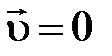) и владела массой m. Следовательно, её импульс 
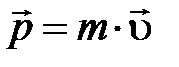так же был равен нулю: 
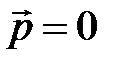. Из этого срочно направляться, снова введённая величина владеет серьёзным свойством, которого нет у скорости ( 
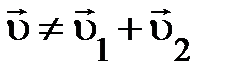), то есть, импульс изолированной совокупности в фиксированной инерциальной совокупности отсчёта сохраняется: 
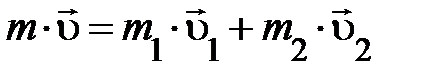. Преобразования в данном абзаце нужно выполнить.
Закон сохранения импульса оказывается нужным при обобщении понятия скорости поступательного перемещения для изолированной совокупности частиц как целого в тех случаях, в то время, когда её нельзя моделировать одной частицей.