Для практических расчетов электрических цепей созданы способы, разрешающие уменьшить количество решаемых уравнений в сравнении с совокупностью уравнений по законам Кирхгофа. Разглядим эти способы.
а) Способ узловых потенциалов. Способ двух узлов.
Количество уравнений по способу узловых потенциалов определяется числом уравнений по первому закону Кирхгофа для разглядываемой электрической цепи. В соответствии с данным способом, нужно сперва выяснить потенциалы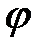 
всех узлов электрической цепи, а после этого посредством закона Ома выяснить токи в ветвях. Наряду с этим один из узлов электрической схемы, что именуют опорным, заземляется, его потенциал 
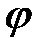делается равен нулю. Узел для заземления выбирается произвольно. Комфортно заземлять узел, номер которого имеет громаднейшее значение в заданной электрической цепи.
Совокупность уравнений по способу узловых потенциалов в виде матрицы будет иметь столько столбцов и строк, столько уравнений нужно записать по первому закону Кирхгофа для разглядываемой электрической цепи. В случае, если в электрической цепи имеется ветвь содержащая лишь совершенный источник ЭДС. Тогда комфортно пронумеровать узлы электрической цепи так, дабы номер узла с громаднейшим значения в заданной электрической цепи, был в узле от которого отходит источник ЭДС. Данный узел принимают за опорный и заземляют. Тогда потенциал узла, в который входит источник ЭДС, будет известным и равным величине ЭДС источника.
Разглядим применение способа узловых потенциалов на примере.
Пример.
Способ узловых потенциалов целесообразно использовать, в то время, когда количество уравнений по первому закону Кирхгофа для электрической цепи получается меньше чем по второму. На рисунке 2.1 представлена электрическая цепь, отвечающая указанным требованиям.
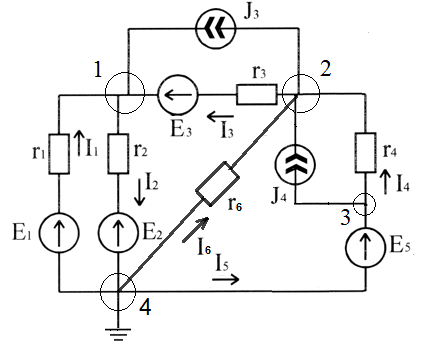
Рисунок 2.1 – Схема электрической цепи для расчета по способу узловых потенциалов
Представленная схема содержит 8 ветвей, 2 из которых содержат источники тока, следовательно, количество уравнений по второму закону Кирхгофа равняется: 8 – 2 – 3 = 3 уравнения.
В заданной цепи четыре узла, следовательно, по первому закону Кирхгофа нужно записать 4 – 1 = 3 уравнения, причем имеется ветвь, содержащая лишь совершенный источник ЭДС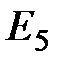 
. В этом случае узел, от которого отходит источник ЭДС 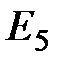, пронумеруем цифрой 4 и примем его за опорный, потенциал которого равен нулю 
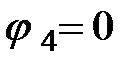. Обозначим заземление 
у ?4 на расчетной схеме. Потенциал узла, в который входит источник ЭДС 
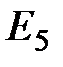, будет известным и равным величине ЭДС источника 
.
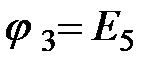Так, остается два малоизвестных потенциала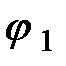 
и 
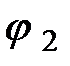, для их нахождения используем совокупность из двух уравнений:
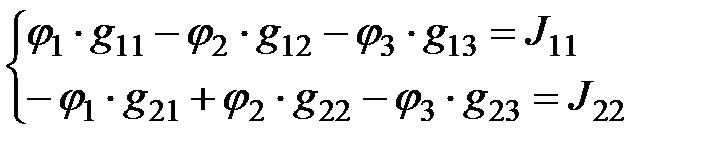, (2.1)
где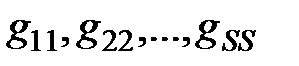 
– личные проводимости узлов 1, 2, …, S, соответственно, каковые определяются как сумма проводимостей ветвей, присоединенных к соответствующему узлу. Для разглядываемой цепи 
; 
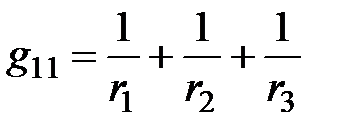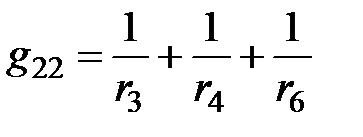. В совокупности уравнений (2.1) у собственных проводимостей узлов по основной диагонали матрицы будут постоянно стоять символы «плюс». В случае, если будет задана такая электрическая цепь, для которой по первому закону Кирхгофа нужно будет записать второе количество уравнений, то совокупность уравнений (2.1) обязана складываться из столбцов и строк, количество которых определяется числом уравнений по первому закону Кирхгофа.
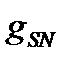– сумма проводимостей ветвей, соединяющих узел S с узлом N, в любой момент в совокупности уравнений (2.1) берется со знаком «минус». Для разглядываемой цепи сумма проводимостей ветвей между узлами 1 и 2, а, следовательно, 2 и 1, есть 
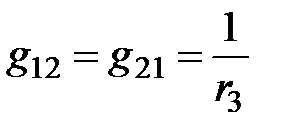. Сумма проводимостей ветвей между узлами 1 и 3, равна нулю, следовательно 
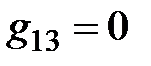. Сумма проводимостей ветвей между узлами 2 и 3 
.
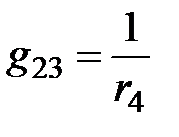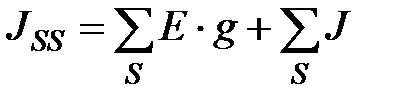, где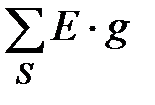 
– алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу S, на их проводимости; наряду с этим со знаком «плюс» берутся те произведения, в ветвях которых ЭДС действуют в направлении узла S, и со знаком «минус», – в направлении от узла S;
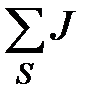– алгебраическая сумма источников тока, присоединенных к узлу S, символ перед 
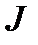определяется в соответствии с правилу, вышеуказанному. В нашем случае 
, 
.
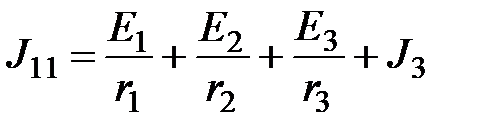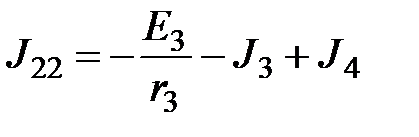Так, в новых обозначениях совокупность уравнений 2.1 примет следующий вид
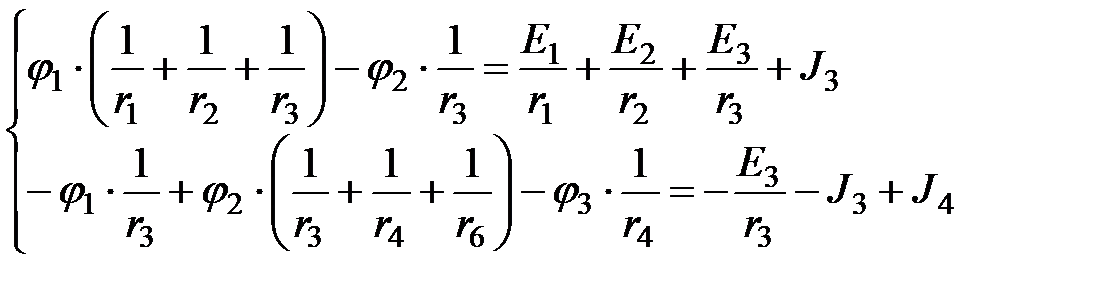. (2.2)
Решив систему (2.2) довольно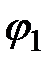 
и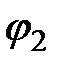 
, полагая известным 
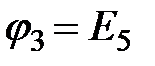, отыщем токи в ветвях электрической цепи.
Токи в ветвях электрической цепи определяются по закону Ома через полученные при ответе совокупности (2.2) потенциалы:
; 
; 
;
; 
; 
.
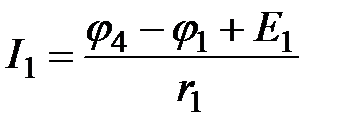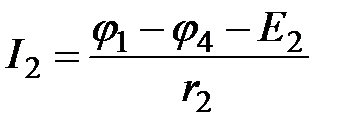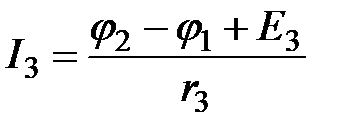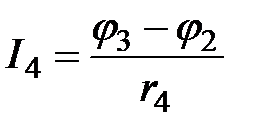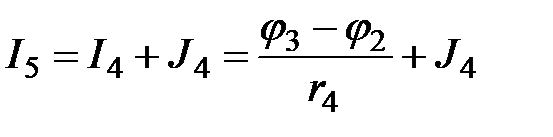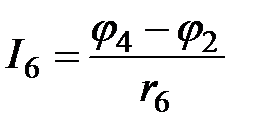Способ двух узлов (частный случай способа узловых потенциалов).
Видятся электрические цепи у которых всего два узла рисунок 2.2. Для расчета токов в таковой цепи самый рациональным способом расчета есть способ двух узлов.
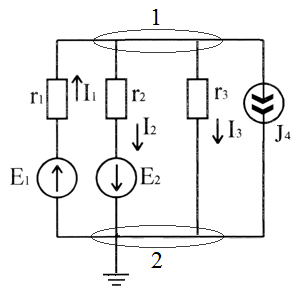
Рисунке 2.2 – Схема электрической цепи, содержащей два узла
Разглядим применение способа двух узлов на примере.
Пример.
Для электрической цепи (рисунок 2.2) по способу узловых потенциалов запишем следующее выражение:
.
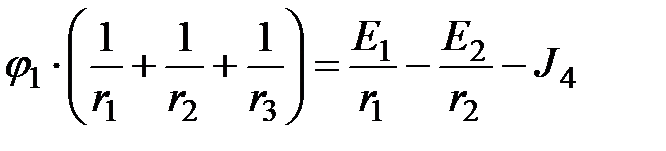Запишем оказавшееся выражение для напряжения 
:
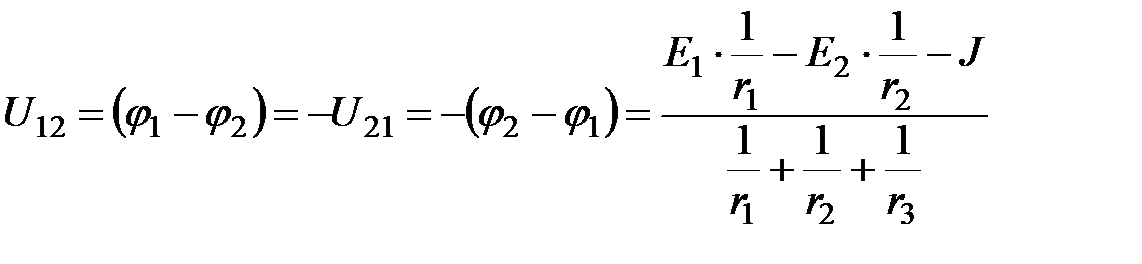. (2.3)
Выражение (2.3) принято именовать способом двух узлов.
Токи в ветвях электрической цепи, определяются по закону Ома следующим образом:
; 
; 
.
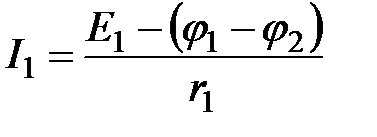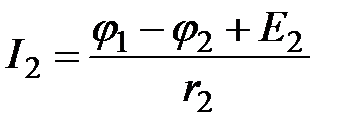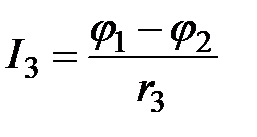б) Способ контурных токов и эквивалентного генератора.
Способ контурных токов кроме этого разрешает уменьшить количество решаемых уравнений в сравнении с совокупностью уравнений по законам Кирхгофа. Количество уравнений по способу контурных токов определяется числом уравнений по второму закону Кирхгофа для разглядываемой электрической цепи. Способ основывается на том свойстве, что ток в любой ветви возможно представлен в виде алгебраической суммы свободных контурных токов, протекающих по данной ветви. В соответствии с данным способом нужно выбрать контурные токи так, дабы любой из них проходил через один источник тока, а оставшиеся контурные токи выбирать проходящими по ветвям, не содержащим источники тока.
Совокупность уравнений по способу контурных токов в виде матрицы будет иметь столько столбцов и строк, столько уравнений нужно записать по второму закону Кирхгофа для разглядываемой электрической цепи. В случае, если в электрической цепи имеется источник тока, то добавится столбец в совокупность уравнений, в случае, если два, то два столбца и т.д.
Разглядим применение способа контурных токов на примере.
Пример.
Способ контурных токов целесообразно использовать, в то время, когда в количество уравнений по второму закону Кирхгофа для электрической цепи получается меньше чем по первому. На рисунке 2.3 представлена электрическая цепь, отвечающая указанным требованиям.
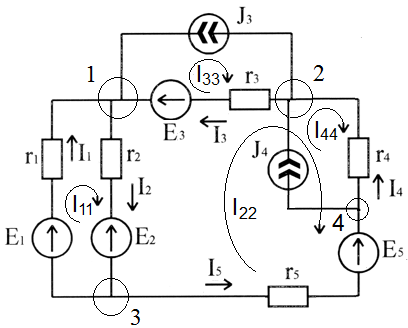
Рисунок 2.3 – Схема электрической цепи для расчета по способу контурных токов
Ответ.
В данной цепи четыре узла, следовательно, по первому закону Кирхгофа нужно записать 4 – 1 = 3 уравнения. Разглядываемая схема содержит семь ветвей, две из которых с источниками тока, следовательно, по второму закону Кирхгофа количество уравнений равняется: 7 – 2 – 3 = 2. Для заданной схемы направления обхода контурных токов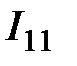 
, 
, 
, 
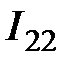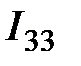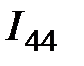забраны по часовой стрелке, причем 
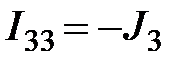, т.к. обход контура не сходится с направлением тока источника тока; 
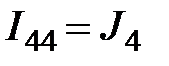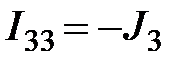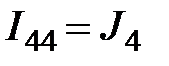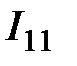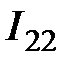, т.к. обход контура сходится с направлением тока источника тока. Так, контурные токи и считаются известными. Следовательно, остается два малоизвестных контурных тока ( и ), для их нахождения используем совокупность из двух уравнений:
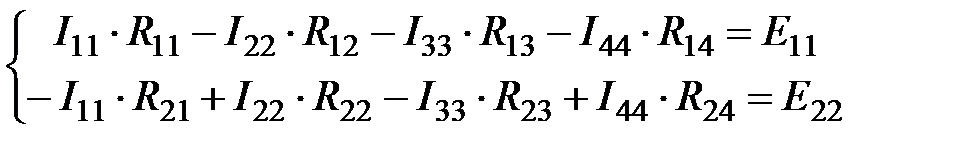(2.4)
где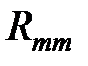 
– собственное сопротивление контура m (сумма сопротивлений всех ветвей, входящих в контур m). Для разглядываемой цепи 
; 
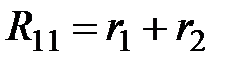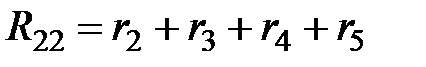. В совокупности уравнений (2.4) у собственных сопротивлений контуров по основной диагонали матрицы будут постоянно стоять символы «плюс». В случае, если будет задана такая электрическая цепь, для которой по второму закону Кирхгофа нужно будет записать второе количество уравнений, тогда и количество уравнений в совокупности (2.4) изменится. Количество строчков в совокупности (2.4) определяется числом уравнений по второму закону Кирхгофа, а количество столбцов равняется сумме числа уравнений по второму закону Кирхгофа и числа источников тока.
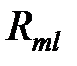– неспециализированное сопротивление контуров m и l, берется со знаком «плюс», в случае, если направления контурных токов в данной ветви совпадают, в обратном случае – берется символ «минус». В разглядываемой схеме неспециализированным сопротивлением между контурами 1 и 2, а, следовательно, 2 и 1, есть 
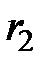. Направление контурных токов в данной ветви не совпадают, следовательно, сопротивление 
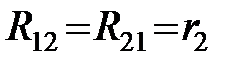войдет в уравнение со знаком «минус». Сопротивления между контурами 1 и 3, и 1 и 4 равны нулю, следовательно, 
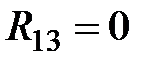и 
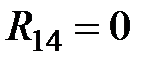. Сопротивление между контурами 2 и 3 
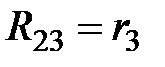. Направление контурных токов в данной ветви не совпадают, следовательно, сопротивление 
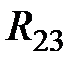войдет в уравнение со знаком «минус». Сопротивление между контурами 2 и 4 
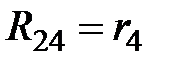. Направление контурных токов в данной ветви совпадают, следовательно, сопротивление 
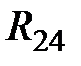войдет в уравнение со знаком «плюс».
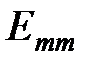– алгебраическая сумма ЭДС, входящих в контур m. Для данной схемы 
, 
.
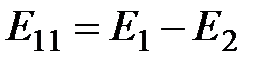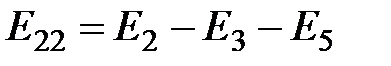Так, в новых обозначениях совокупность уравнений 2.4 примет следующий вид
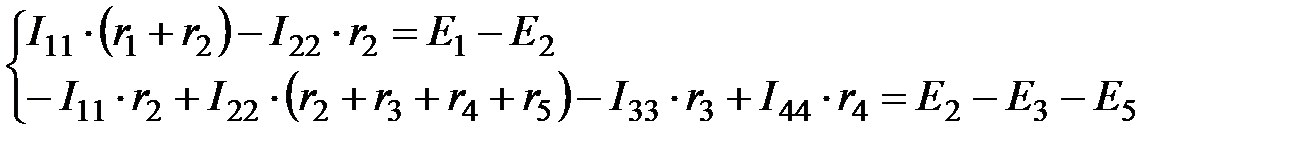. (2.5)
Решив систему (2.5) довольно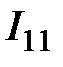 
и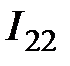 
, полагая 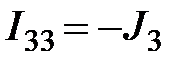и 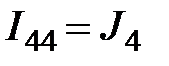известными, отыщем токи в ветвях электрической цепи.
Токи в ветвях электрической цепи, через контурные токи определяются следующим образом:
; 
; 
;
; 
.
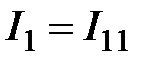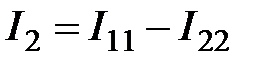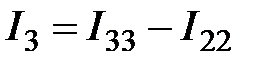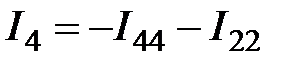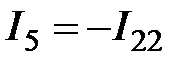Способ эквивалентного генератора в отличие от представленных выше разрешает выяснить ток, лишь в одной выбранной ветви, методом упрощения оставшейся части электрической цепи в одноконтурную неразветвленную цепь. По отношению к выделенной ветви другую часть цепи заменяют эквивалентным источником ЭДС – генератором. ЭДС этого генератора равна напряжению холостого хода на зажимах выделенной части цепи, к каким будет подключаться ветвь с определяемым током. Внутреннее сопротивление генератора будет равна входному сопротивлению по отношению к зажимам выделенной ветви.
Последовательность расчета по способу эквивалентного генератора.
1. Выделить в расчетной цепи ветвь, ток которой нужно выяснить. Другую часть схемы представить в виде источника ЭДС и внутреннего сопротивления. Выбрать хорошее направление тока в ветви.
2. Отсоединив выделенную ветвь, выяснить любым из ранее изученных способов напряжение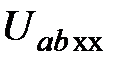 
на зажимах оставшейся части схемы, к каким будет подключаться ветвь с определяемым током.
3. Выяснить эквивалентное входное сопротивление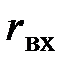 
по отношению к зажимам выделенной ветви. Наряду с этим источники энергии заменить их внутренними сопротивлениями и вычислять сопротивления источников ЭДС равными нулю, а сопротивления источников тока равными бесконечности.
4. Выяснить по закону Ома ток в взятой неразветвленной цепи:
,
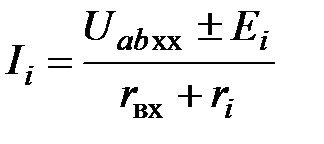где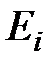 
, 
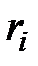– параметры ветви с искомым током.
Пример.
Разглядим применение способа эквивалентного генератора для электрической цепи, представленной на рисунке 2.4.
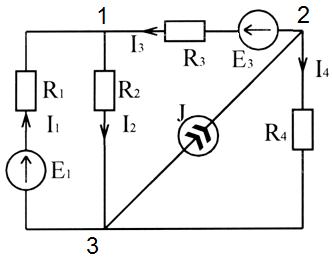
Рисунок 2.4 – Схема электрической цепи для расчета по способу эквивалентного генератора
При расчетах нужно выяснить ток в третьей ветви. Все параметры элементов электрической цепи, и ее топология считаются известными.
Ответ.
1. Выделим в расчетной цепи ветвь с током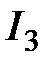 
, что будем определять. Другую часть схемы представим в виде источника ЭДС внутренним 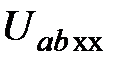сопротивлением и напряжением 
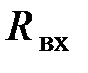(рисунок 2.5). Выберем хорошее направление тока в третьей ветви.
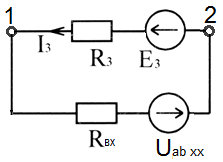
Рисунок 2.5 – Эквивалентная схема замещения
3. Отсоединим третью ветвь и определим любым из ранее изученных способов напряжение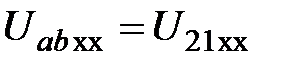 
на зажимах оставшейся части схемы (рисунок 2.6).
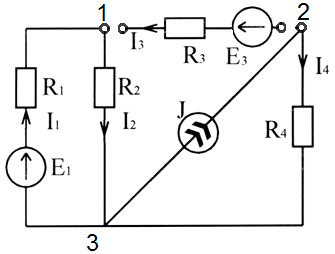
Рисунок 2.6 – Схема электрической цепи для расчета по способу эквивалентного генератора
По окончании отключения третьей ветви три электрическая цепь распадается на две свободные. Одна с источником ЭДС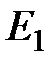 
, вторая источником тока 
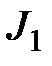. При таких условиях отыскать напряжение 
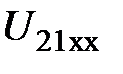возможно по закону Ома. Условно заземлим узел 3, тогда 
.
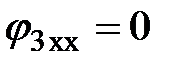Отыщем потенциал точки 1 через потенциал узла 3
.
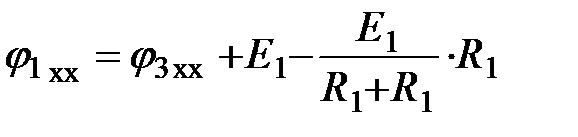Потенциал точки 2 через потенциал точки 3
.
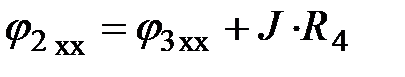Так,
.
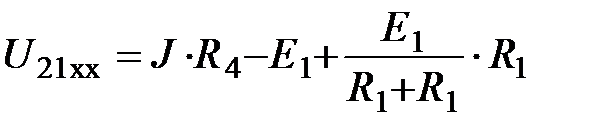4. Определим эквивалентное входное сопротивление 
по отношению к зажимам выделенной ветви. Наряду с этим источники энергии заменим их внутренними сопротивлениями и вычисляем сопротивления источников ЭДС равными нулю, а сопротивления источников тока равными бесконечности
.
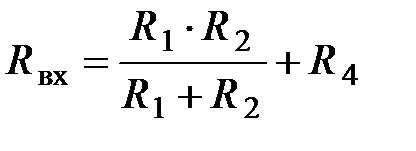5. Определим по закону Ома ток в третьей ветви:
.
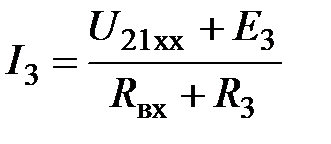в) Способ наложения.
Способ наложения применим лишь для расчета линейных цепей, параметры элементов которых не зависят от значений протекающего тока либо приложенного напряжения. Для расчетов цепей способом наложения составляют столько частных схем, сколько свободных источников энергии имеет исходная цепь. В личной схеме оставляется лишь один источник, все остальные заменяют их внутренними сопротивлениями. Результирующий ток ветви равен алгебраической сумме частных токов, вызванных действием каждого источника в отдельности. При исключении совершенных источников напряжения вместо источника ставится короткозамкнутая перемычка, что соответствует ЭДС, равной нулю при нулевом внутреннем сопротивлении. Ветвь с источником тока, напротив, размыкается, что соответствует нулевому току при нулевой проводимости.
При расчете частных схем токи, протекающие в ветвях, обозначают двумя индексами. Нижний индекс показывает номер ветви, в которой определяют ток, а верхний – номер источника, действием которого вызывается ток. К примеру,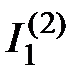 
? ток первой ветви, вызываемый действием второго источника. При расчете частных схем довольно часто приходится рассчитывать токи в параллельных ветвях 
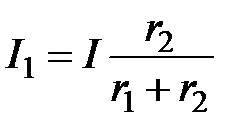и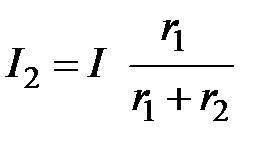 
(см. практическое занятие 1).
Разглядим применение способа наложения на примере.
Пример.
Способом наложения целесообразно пользоваться при расчетах электрической цепи, в которой содержащих один либо два, в крайнем случае, три источника электроэнергии. На рисунке 2.7 представлена электрическая цепь с двумя источниками энергии, отвечающая указанным требованиям.
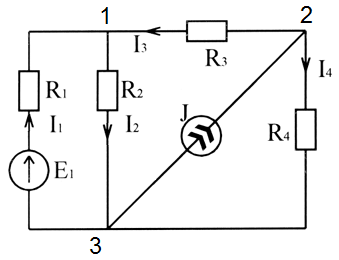
Рисунок 2.7 – Схема электрической цепи для расчета по способу наложения
Для нахождения токов в схеме рисунка 2.7 способом наложения определяют токи в частных схемах, приведенных на картинках 2.8 и 2.9.
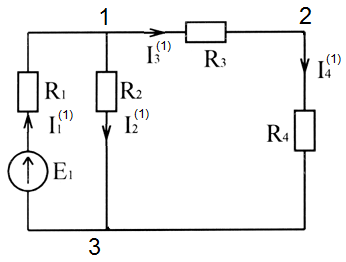
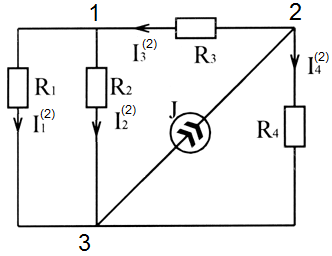
Рисунок 2.8 Рисунок 2.9
Для схемы рисунка 2.8:
; 
; 
.
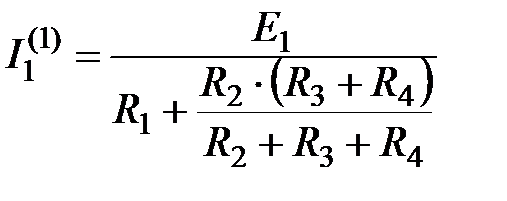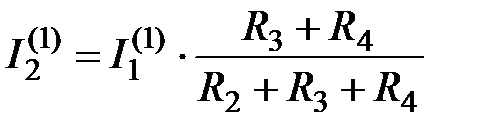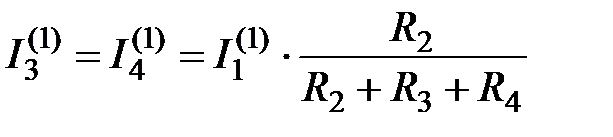Для схемы рисунка 2.9:
; 
;
; 
.
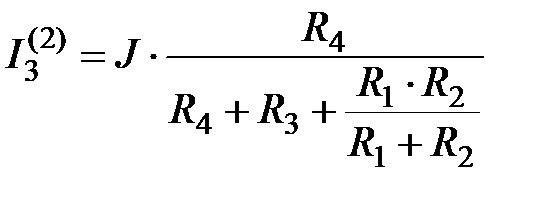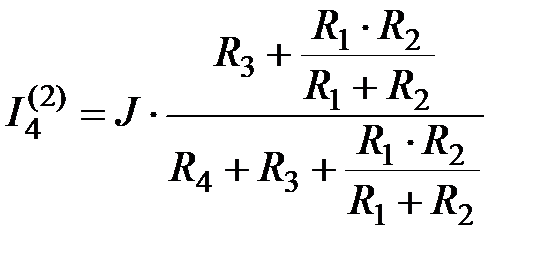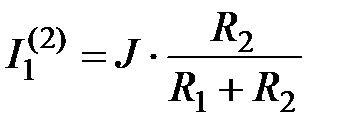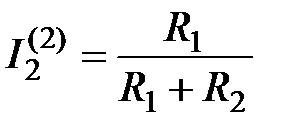направляться подчернуть, что при действии в электрической схеме одного источника электроэнергии, как продемонстрировано картинках 2.8 и 2.9, в ветвях схемы текут частичные токи. Их направление обусловлено направлением действующего в электрической цепи источника электроэнергии. Так, на рисунке 2.8 направление тока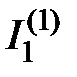 
обусловлено направлением источника ЭДС 
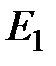. Из рисунка 2.8 видно, что ток 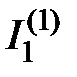подтекает к узлу 1, в котором он разделяется на 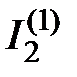ток 
и ток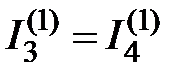 
, по окончании чего эти токи подтекают к узлу 2, где они опять объединяются в ток 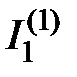. На рисунке 2.9 направление токов 
, 
, 
, 
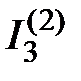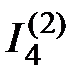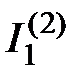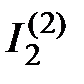обусловлено направлением источника тока 
.
Так, токи в исходной электрической цепи, определятся на базе частичных токов следующим образом:
.
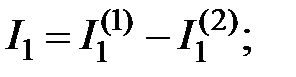
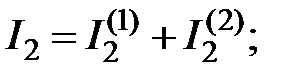
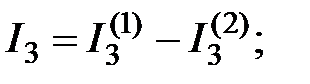
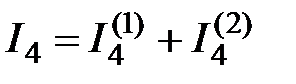Символ «минус» стоит у первого и третьего тока, поскольку их частичные токи при действии двух источников энергии имеют различные направления. Частичные токи второго и четвертого тока имеют однообразные направления, исходя из этого в уравнениях результирующего тока стоит символ «плюс».
Выводы по лекции
Для расчета токов ветвях электрицеской цепи не считая законов Кирхгофа возможно использовать способ узловых потенциалов, способ контурных токов, способ наложения, способ эквивалентного генератора. Число уравнений для способа узловых потенциалов такое же как по первому закону Кирхгофа, в случае, если схема содержит всего два узла возможно использовать способ двух узлов. Число уравнений для способа контурных токов такое же как по второму закону Кирхгофа. Способ наложения целесообразно применять, в то время, когда в электрической цепи содержится не более трех источников электроэнергии. В случае, если нужно вычислить ток в одной ветви возможно применять способ эквивалентного генератора.
Вопросы для самопроверки
1. Сформулировать ключевые принципы способа узловых потенциалов.
2. Каковы особенности применения способа узловых потенциалов для схем, содержащих лишь совершенный источник ЭДС в любой из ветвей?
3. Как отыскать токи в ветвях по способу двух узлов?
4. Охарактеризуйте главные этапы способа контурных токов.
5. Каковы особенности применения способа контурных токов для схем, содержащих источник тока?
6. В чем преимущества и недочёты способа наложения?
7. Изложите сущность способа эквивалентного генератора?