Тут не может быть верного либо неверного ответа. Мы желаем знать Ваше суждение об интенсивности запахов. Имеется вопросы?”1.
На протяжении опыта стандарт предъявляется перед каждым переменным стимулом. Стивенсом (1956) были эмпирически выведены следующие правила организации опыта по оценке размеров с модулем, разрешающие устранить влияния посторонних факторов на итог измерения:
1. Применяйте стандарт, уровень которого не воспринимается наблюдателем как экстремальная точка в последовательности интенсивностей, другими словами применяйте эргономичный стандарт, что, образно говоря, наблюдатель “имел возможность бы подержать в руках”.
2. Предъявляйте такие переменные, каковые были бы как выше, так и ниже стандарта.
3. Обозначайте стандарт числом, подобным 10, дабы им легко было оперировать.
4. Назначьте число лишь стандарту и предоставьте наблюдателю полную свободу решать, как ему назвать переменный стимул. К примеру, не информируйте наблюдателю, что самый не сильный переменный стимул будет назван 1, либо что самый громкий будет назван каким-нибудь вторым числом. В случае, если экспериментатор присвоит число более чем одному стимулу, он введет собственного рода принуждение, которое заставляет наблюдателя создавать суждения на более “сырой” — интервальной шкале, а не на шкале взаимоотношений.
5. Применяйте лишь один уровень стандарта в серии, но в целом изучении используйте разные стандарты, поскольку рискованно делать выводы о форме функции, взятой на базе данных лишь с одним стандартом.
6. Случайный порядок предъявления. С неопытным наблюдателем это отлично, однако начинайте с отношения громкости, которое не экстремально и которое, следовательно, легко оценить.
7. Делайте опыт маленьким — около 10 мин.
8. Пускай наблюдатель сам себе предъявляет стимулы. Тогда он сможет трудиться своим темпом и это разрешит ему быть более внимательным.
9. Так как оценки смогут очень сильно отклоняться от оценок “среднего” наблюдателя, то нужно применять группу наблюдателей, которая велика, чтобы получить при обработке устойчивую медиану.
В способе оценки размеров шкальные значения измеряемого субъектом показателя находятся в ответах испытуемых и смогут быть представлены медианой либо геометрическим средним всех оценок группы испытуемых, относящихся к каждому из стимулов. Медиана есть более неотёсанной, чем геометрическое среднее, мерой центральной тенденции. Геометрическое среднее в отличие от среднего арифметического логически более обосновано, т.к. в следствии измерения в большинстве случаев получается нелинейная психофизическая функция типа R = aYn. Геометрическое среднее определяется равенством (1). При солидном числе измерений рекомендуется логарифмический вариант равенства (2).
Разглядим пример из вышеупомянутой работы Энгена (1971), в которой любой из испытуемых два раза оценивал 7 разных концентраций запаха амилацетата, разведенного в диэтилфтолате. В качестве модуля, которому приписывалось значение 10, предъявлялась концентрация 12.50. Геометрические средние оценок представлены в табл. 2.
Представление этих данных в линейных координатах говорит о том, что полученная психофизическая функция нелинейна и характеризуется замедляющимся ускорением: лишь при малых концентрациях амилацетата прирост запаха опережает рост концентрации. Будучи представлена в двойных логарифмических координатах, эта функция отлично аппроксимируется прямой с наклоном
Таблица 2
Субъективная шкале запаха амилацетата, разведенного в без сомнений
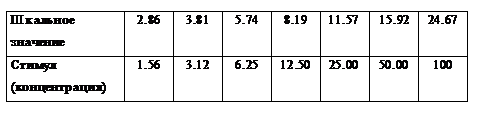 |
самый существенным недочётом способа оценки размеров с заданным модулем возможно зависимость экспоненты степенной функции от места заданного модуля в стимульном последовательности. Наличие таковой зависимости (Энген, 1971) очень не очень приятно тем, что ставит под сомнение экспоненту степенной функции как особую чёрта континуума и модальности. Но существование таковой зависимости далеко не всегда подтверждается опытами (Стивенс, 1956; Джонс и Восков, 1966).
2. Способ оценки размеров со свободным модулем.
В этом варианте способа мысль о независимости суждений испытуемого от выбора модуля взяла логическое завершение: никакой стимул не объявляется стандартным, не вводятся никакие ограничения при выборе чисел для ответа. Единственное требование к испытуемому — стараться при ответе применять числа, совершенно верно высказывающие величину позванного стимулом ощущения. В большинстве случаев стимулы предъявляются рандомизированно и в собственном для каждого испытуемого порядке. Перед началом опыта испытуемому дают пара (3—5) тренировочных проб.
Особенности этого варианта способа иллюстрируются в работе Кайн (1968) по оценке интенсивности запаха пентанола. 15 испытуемых оценивали каждую из 7 концентраций пентанола по 2 раза. Инструкция испытуемым:
“Вам будет предъявляться в нерегулярном порядке последовательность тюбиков, содержащих одинаковый по качеству запах, но отличающихся по его интенсивности. Ваша задача — информировать мне об интенсивности запаха, характеризуя его соответствующим числом. В то время, когда Вы понюхаете тюбик, обозначьте интенсивность запаха числом — любым числом, которое Вам думается подходящим. После этого я буду поочередно предъявлять Вам другие тюбики, и Вы станете каждому приписывать число. Попытайтесь, дабы отношения между приписываемыми числами соответствовали отношениям между интенсивностями запахов. В противном случае говоря, числа должны быть пропорциональны интенсивности исследуемого запаха. Не забывайте, что вы имеете возможность применять любое число, ограничений в выборе числа не существует. Верного либо неправильного ответа тут быть не имеет возможности. Нас интересует Ваше суждение об интенсивности запаха. Имеется вопросы?”1.
Полученные в опытах Кайн эти представлены в табл. 3.
Таблица 3
Личные оценки концентраций пентанола (Кайн, 1968)
 |
Казалось бы, что геометрическое среднее каждой колонки матрицы может рассматриваться как значение на субъективной шкале силы запаха. Но в силу отсутствия каких-либо ограничений в выборе модуля, применяемого различными испытуемыми, числовые области смогут очень сильно расходиться. Эта вариативность должна быть устранена до сглаживания групповых данных.
Стивенс (1956) предлагает применять несложную процедуру приведения оценок каждого испытуемого, данных каждому из стимулов, к единой величине методом умножения на подходящий коэффициент. Процедура обработки “сырых” данных включает следующие этапы: 1) определение медианы либо геометрического среднего двух оценок каждого стимула каждым испытуемым; 2) выбор единого шкального значения оценки стимула (нужно брать его для середины стимульного последовательности) и приведение всех оценок каждого испытуемого к единому масштабу через умножение на соответствующий коэффициент; 3) вычисление геометрического среднего либо медианы для каждого стимула по приведенным оценкам всех испытуемых даст шкальные значения измеряемого показателя.
Преимуществом предлагаемого Стивенсом метода обработки есть его простота. Недочёт этого метода пребывает в том, что определение коэффициента для приведения личных оценок осуществляется на базе суждений лишь об одном стимуле. Следовательно, в этом методе не учитывается личная несистематичность в применении чисел, в силу которой оценка испытуемым отдельного стимула может заметно выпадать из неспециализированной закономерности. В случае, если коэффициент приведения вычисляется по оценке конкретно для того чтобы стимула, то возрастает неточность в сглаживании групповых оценок всех стимулов.
Энген (1971) предлагает более громоздкий, но и более корректный метод первичной обработки экспериментальных данных, в котором учитывается как меж-, так и внутрииндивидуальная вариативность суждений. Его метод складывается из 6 этапов:
1. Выяснить логарифм каждой численной оценки стимула.
2. Вычислить логарифм геометрического среднего оценок каждого стимула в отдельности каждым испытуемым.
3. Отыскать логарифм геометрического среднего оценок каждым испытуемым всех стимулов, отыскать среднее каждого последовательности (см. табл. 3).
4. Выяснить среднее всех размеров, вычисленных на 3-м этапе — логарифм неспециализированного геометрического среднего оценок всех стимулов всеми испытуемыми в матрице “сырых” данных.
5. Вычесть величину логарифма неспециализированного геометрического среднего (п.4) из логарифма личного геометрического среднего (п.3).
6. Сложить разности, полученные в п.5, с соответствующими значениями логарифмов геометрического среднего оценок испытуемым каждого стимула (п.2).
Итоги таковой первичной обработки данных, приведенных в табл. 3, продемонстрированы в табл. 4.
Таблица 4
Скорректированные оценки испытуемых, представленные в табл. 3 (по Энгену, 1971)
 |
Цель, которая достигается этим методом обработки, пребывает в уменьшении разброса личных данных около главной функции, но не воздействует на ее параметры. Для получения шкальных значений необходимо вычислить среднее для каждой колонки, антилогарифм которого и есть геометрическим средним оценок группой испытуемых данного стимула. Отысканные так геометрические средние употребляются при определении вида психофизической зависимости.
В том случае, если эта зависимость подчиняется степенному закону Z = kS?при изображении ее в двойных логарифмических координатах, она должна быть прямой линией. В случае, если же исследуемая зависимость подчиняется закону Фехнера Z = klogS, она возможно представлена прямой лишь в том случае, если логарифмический масштаб берется лишь для шкалы физического параметра стимулов, а шкала суждений остается линейной.
Как было отмечено выше, прямая эргономичнее (несложнее) с позиций наилучшей подгонки к экспериментальным точкам и подбора математического описания взятой зависимости. В большинстве случаев подгонка осуществляется или “на глазок”, что дает неотёсанное приближение при разбросе точек около подлинной линии регрессии, или способом мельчайших квадратов, разрешающим обеспечить наилучшую аппроксимацию, в случае, если заблаговременно известен вид зависимости.
Литература
Главная
1. Джелдард Ф.А. Сенсорные шкалы//Хрестоматия по восприятию и ощущению/Под ред. Ю.Б. Гиппенрейтер, М.Б. Михалевской. М.: Изд-во Моск. ун-та, с. 1975.
2. Стивенс С.С. Психофизика сенсорной функции//Хрестоматия по восприятию и ощущению/Под ред. Ю.Б. Гиппенрейтер, М.Б. Михалевской. М.: Изд-во Моск. ун-та, 1975.
Дополнительная
1. Вудсвортс Р., Шлосберг Г. Психофизика II. Способы шкалирования//Неприятности и способы психофизики/Под ред. А.Г. Асмолова, М.Б. Михалевской. М.: Изд-во Моск. ун-та, 1974. с. 174—228.
2. Стивенс С.С. О психофизическом законе//Неприятности и способы психофизики/Под ред. А.Г. Асмолова, М.Б. Михалевской. М.: Изд-во Моск. ун-та, 1974.
3. Harper R.S., Stevens S.S. A Psychological Scale of Weight and a Formula for its Derivation//Amer. J. Psychol. 1948. Vd. 61. P. 343—351.
4. Stevens S.S. The Direct Estimation of Sensory Magnitudes: Loudness//Amer. J. Psychol. 1956. Vd. 69. P. 1—25.
Методические советы по исполнению учебного задания по теме
“Способы прямой оценки”
Задание 1. Построение психофизической функции высоты звукового тона
Цель задания. Фактически ознакомиться с способом установления заданного отношения, выстроить психофизическую функцию высоты звукового тона.
Методика
Аппаратура. Задание выполняется на IBM-совместимом персональном компьютере. Для предъявления звуковых стимулов употребляются особая звуковая плата типа “Sound Blaster” и головные телефоны. Для исполнения учебного задания употребляется компьютерная программа sscal.exe.
Стимуляция. Стимулами являются бинаурально предъявляемые тональные звуковые сигналы в диапазоне от 125 до 12000 Гц и интенсивностью около 80 дБ (УЗД). Употребляются 8 стандартных стимулов: 125, 250, 500, 1000, 2000, 4000, 6000, 8000 Гц.
Испытуемые. Любой студент сперва трудится как испытуемый, а после этого обрабатывает собственные оценки и сооружает по ним психофизическую зависимость. Для получения групповых данных испытуемые должны объединиться в группу не меньше 7—10 человек.
Процедура. Шкалирование производится способом оценки заданного отношения в вариантах фракционирования (деления на 2) и мультипликации (умножения на 2). Опыт складывается из 2-х серий — “деление на 2” и “умножение на 2”. В первой серии употребляются 7 стандартных стимулов: частотой 250, 500, 1000, 2000, 4000, 6000 и 8000 Гц. Во второй — 125, 250, 500, 1000, 2000, 4000, 6000 Гц. Стандартные стимулы предъявляются в случайном порядке, любой по 5 раз. Оценка заданного отношения производится способом установки, в то время, когда, регулируя частоту переменного стимула, испытуемый подбирает подходящий переменный стимул.
Любая проба начинается с предъявления на экране монитора ее порядкового номера (от 1 до 35). Затем, надавив на клавишу на клавиатуре компьютера, испытуемый обязан прослушать звучание стандартного стимула. Для прекращения предъявления стандартного стимула направляться надавить клавишу . Регулировка частоты переменного стимула (от частоты стандарта) осуществляется клавишами управления перемещением курсора — , , для увеличения и уменьшения частоты, соответственно. Нажимая на эти клавиши, испытуемый может изменять частоту звукового сигнала: чем продолжительнее нажимаешь на клавишу, тем стремительнее изменяется его частота. В любую секунду испытуемый может возвратиться к прослушиванию стандартного стимула, надавив еще раз на . Окончание подбора переменного стимула, находящегося в заданном отношении к стандартному, подтверждается нажатием на клавишу .
Между сериями устраивается 5-минутный паузу.
Обработка результатов. По окончании окончания опыта испытуемому выдается распечатка личных результатов, в которой для каждой серии (умножение и деление на 2) приводятся геометрические средние его оценок стандартных стимулов.
На протяжении предстоящей обработки личных результатов каждому студенту направляться выполнить следующее:
1. Занести полученные данные в таблицу.
2. Представить полученные данные в линейных координатах на 2-х отдельных графиках (рис.1 и 2): абсцисса — частота стандартного стимула, ордината — частота стимула, оцененного находящимся в заданном отношении (1/2, 2) к стандартному.
4. То же самое повторить в двойных логарифмических координатах (рис. 3 и 4). Посредством линейного регрессионного анализа вычислить параметры регрессионных прямых для двух серий опыта и выстроить соответствующие прямые на рис. 3 и 4.
Для исполнения регрессионного анализа целесообразно воспользоваться статистическим пакетом “Stadia”. В редакторе данных частоты стандартного стимула заносятся в первую переменную (это будут значения X ), а оценки испытуемого — во вторую (это будут значения Y). После этого переходят в меню статистических процедур (F9) и выбирают опцию “Несложная регрессия (тренд)”. Войдя в нее, необходимо указать номера переменных (1, 2), а после этого указать тип функции для построения регрессии — линейная. Затем программа выстроит для вас математическую модель ваших данных, воображая их в виде уравнения прямой: Y = a0 + a1*X. Взяв коэффициенты a0и a1, возможно легко выстроить на графике аппроксимирующую прямую, проходящую через 7 экспериментальных точек. Статистическая оценка адекватности сделанной линейной аппроксимации приводится внизу экрана.
5. Выстроить психофизическую зависимость, применяя результаты 2-х серий опыта — “деление на 2” и “умножение на 2”. Для этого поступим подобно С. Стивенсу и соавт. (1937) и примем чувство высоты тона 1000 Гц за точку отсчета, присвоив ей величину 1000 “мел”. Для нахождения нужных значений на оси абсцисс психофизической функции возможно воспользоваться или графиками, выстроенными на рис. 3 и 4, или решить ту же задачу более совершенно верно — аналитически.
С целью этого возможно обратиться к уравнениям регрессионных прямых и выполнить все вычисления по формуле вручную либо еще раз воспользоваться программой “Stadia”. Формально это указывает, что по взятому уравнению регрессионной прямой (геометрической модели оценок испытуемого) необходимо отыскать малоизвестные X по известным Y. С целью проведения расчетов необходимо опять возвратиться в меню статистических способов и, выбрав ту же опцию (“Линейная регрессия”), указать второй порядок переменных — 2,1. Это будет означать , что в качестве X мы выбираем полученные оценки испытуемого, а в качестве Y — частоту стандарта. По окончании расчета нового регрессионного уравнения возможно отыскать все нужные точки на оси X конструируемой психофизической функции.
Нанеся 8—10 точек на график психофизической функции возможно попытаться соединить их плавной кривой и прикинуть “на глазок” вид взятой функции. Для более строгой оценки взятой зависимости направляться снова обратиться к статистической программе “Stadia” и, воспользовавшись способами регрессионного анализа, оценить ее как соответствующую логарифмической либо степенной функции. Степень соответствия возможно оценить по минимуму коэффициента и максимуму корреляции доверительного интервала и стандартного отклонения коэффициентов а0и а1.
6. Выстроить психофизическую функцию по групповым данным, для чего вычислить геометрические средние по 7—10 личным оценкам, причем в каждую группу не должны входить однообразные личные эти.
Обсуждение результатов.
1. Сопоставив деления и данные умножения, оценить обоснованность взятой субъективной шкалы, как шкалы взаимоотношений.
2. Сделать вывод о приложимости одного из известных психофизических законов к взятым экспериментальным данным.
3. Сравнить личную и групповую шкалы и оценить их адекватность литературным данным (см. статью Р. Вудвортса и Г. Шлосберга в кн. “Неприятности и способы психофизики”. Под ред. А.Г. Асмолова, М.Б. Михалевской, с. 183-186).
ЧАСТЬ III
МНОГОМЕРНОЕ ШКАЛИРОВАНИЕ
Глава 1. ФАКТОРНЫЙ АНАЛИЗ
Введение
Факторный анализ (ФА) принадлежит к числу таких способов, каковые будучи созданными в рамках запросов одной науки, потом купили более широкое междисциплинарное значение. Заслугой психологии можно считать разработку конкретно для того чтобы способа. Исторически появившийся в лоне психометрики, ФА на данный момент получил статус общенаучного способа и обширно распространен не только в психологии, но и в нейрофизиологии, социологии, политологии, статистике и экономике. Исходя из этого не следует удивляться, в случае, если на вопрос к математику, что такое ФА, вы получите ответ, что данный способ понижения размерности корреляционной матрицы, а экономист добавит, что ФА употребляется им как средство визуализации многопараметрического объекта экономического анализа.
ФА как общенаучный способ, взявший к настоящему времени солидное математико-статистическое обоснование, имеет непростую историю, начиная с полного отказа математиков признать сокровище применяемого психологами в известной степени нестрогого и зависящего от мастерства исследователя метода до необходимого включения разных вариантов ФА в любую какое количество-нибудь известную компьютерную статистическую программу. Главные идеи ФА (но, как и других способов многомерного анализа данных) были заложены в трудах известного антрополога и английского психолога Ф. Гальтона (1822—1911), основателя евгеники, внесшего кроме этого солидный вклад в изучение личных различий. В разработку ФА внесли вклад многие ученые и лишь на русском опубликовано более 10 монографий, посвященных конкретно ФА, но психологи должны быть особенно признательны трем своим сотрудникам, с именами которых связаны внедрение и разработка ФА в психологию — это Ч. Спирмен (1904, 1927, 1946), Л. Терстоун (1935, 1947, 1951) и Р. Кеттел (1946, 1947, 1951). Помимо этого, нельзя не упомянуть еще трех ученых — философа и английского математика К. Пирсона, в значительной мере развившего идеи Ф. Гальтона, американского математика Г. Хоттелинга, создавшего современный вариант способа основных компонент, и известного британского психолога Г. Айзенка, обширно применявшего ФА для создания психотерапевтической теории личности.
Нужно подчернуть, что в силу опытных установок авторов в литературе на русском (К. Иберла, 1980; Г. Харман, 1972) ФА значительно чаще излагается как один из способов математической статистики, а ориентированное на психологов изложение — скорее исключение, чем правило (Дж. Ким, Ч. Мьюллер, 1989; Я. Окунь, 1972). В данной главе ФА будет излагаться как один из способов психотерапевтического шкалирования и многомерного анализа данных. Помимо этого, в отличие от вторых авторов, в силу последовательности обстоятельств обрисовывавших в основном центроидный способ ФА, мы уделим особенное внимание более современным и компьютеризованным процедурам применения ФА. По возможности мы будем исключать экскурсы в математические базы той либо другой процедуры, а сосредоточимся на описании главных этапов работы с эмпирическими данными и их изменением на протяжении ФА. В силу специфики курса “Психотерапевтические измерения” в Общем психотерапевтическом практикуме изложение материала будет сопровождаться иллюстрациями применения 2-х статистических программ — “Stadia” и SPSS.
§ 1. Область применения факторного анализа
Необходимость применения ФА в психологии как одного из способов многомерного количественного описания (измерения, анализа) замечаемых переменных первым делом направляться из многомерности объектов, изучаемых отечественной наукой. Сразу же определим, что под многомерным понятием объекта мы будем осознавать итог его оценивания по нескольким разным и значительным для его описания чертям-измерениям, т.е. присвоение ему сходу нескольких числовых значений. Из этого в полной мере конечно следуют два вопроса жизни и смерти: как значительны и разны эти применяемые характеристики. Первый вопрос связан с полнотой и всесторонностью описания объекта психотерапевтического измерения, а второй (в основном) — с выбором некоего минимально разумного количества этих черт. Поясним сообщённое выше на примере. Чем отличается хороший, профессионально сделанный психотерапевтический опросник от бессчётных “полупродуктов-полушуток”, во множестве публикуемых в периодической печати для широкой публики либо в книгах непрофессионалов-любителей? В первую очередь тем, что в первом случае объект психотерапевтического измерения (конструкт) описывается разносторонне и полно, и, помимо этого, в нем не содержится лишних, не относящихся к делу (т.е. “не трудящихся” на ту либо иную шкалу) вопросов. Так, при применении способов многомерных измерений психотерапевтических черт самый серьёзны две неприятности — обрисовать объект измерения всесторонне и, в также время, компактно. С известной долей обобщения возможно заявить, что это одни из главных задач, решаемых ФА.
Ясно, что информативность многомерного описания объекта отечественного изучения возрастает с повышением количества применяемых показателей либо измерительных шкал. Но весьма тяжело выбрать сходу и значительные, и свободные друг от друга чёрта. Данный выбор иногда непрост и продолжителен. В большинстве случаев, исследователь начинает с заведомо избыточного количества показателей, и в ходе работы (к примеру, по созданию нового опросника либо анализу экспериментальных данных) сталкивается с необходимостью адекватной интерпретации громадного количества взятых данных и их компактной визуализации. Разбирая полученные эти, исследователь подмечает тот факт, что оценки изучаемого объекта, полученные по некоторым шкалам, сходны между собой, а вдруг оценить это сходство количественно и подсчитать коэффициент корреляции, то он может оказаться высоким. Иначе говоря появляется вопрос о том, что многие характеристики (т.е. переменные, по которым производилось измерение отечественного объекта), возможно, в некоей степени дублируют друг друга, а вся полученная информация в целом избыточна. Внимательный исследователь, кроме того незнакомый с базами ФА, сразу же может сообразить, что за связанными между собой (коррелирующими) переменными, по-видимому, стоит влияние некоей скрытой, латентной переменной, благодаря которой возможно растолковать замечаемое сходство взятых оценок. Часто эту гипотетическую латентную переменную именуют причиной. Примерно такаялогика вынудила Чарлза Спирмена, психолога Оксфордского университета, на протяжении анализа результатов тестирования свойств учеников британских школ предположить существование единого, главного фактора интеллектуального развития человека, воздействующего на бессчётные показатели разнообразных интеллектуальных тестов. Так, в далеком прошлом узнаваемый способ научного познания — обобщение —приводит нас к необходимости и возможности выделения факторов как переменных более неспециализированного, более большого порядка. Часто обобщение разрешает по-новому посмотреть на полученные эти, подметить те связи между исходными чертями (переменными), каковые ранее были не очевидны, а затем выйти на более большой уровень понимания сущности измеряемого объекта.
Для того чтобы рода обобщение (т.е. сокращение размерности взятых данных) позволяет применять весьма замечательное средство научного анализа — графическое представление взятых данных. Ясно, что сокращение размерности результатов многомерного измерения какого-либо объекта до двух-трех разрешит исследователю в весьма наглядной и компактной форме представить целый количество взятых данных, выйдя за рамки логического анализа массы цифр, собранных в огромную таблицу. Имея в виду ответственное значение наглядно-образного мышления, тяжело переоценить преимущества пространственного (графического) осмысления разбираемых данных. Так, ФА может рассматриваться и как средство компактной визуализации данных.
Выделение на протяжении анализа данных неспециализированного (для последовательности переменных) фактора разрешает решать исследователю еще одну сложную задачу — оценивать некую скрытую от яркого наблюдения переменную (фактор) опосредованно, косвенно — через ее проявление (влияние) во многих других, прямо измеряемых переменных. Подобным образом в психодиагностике личности были обнаружены, экстрагированы и измерены многие личностные конструкты, к примеру: хороший конструкт Айзенка импульсивность, оцениваемый в тесте EPI по ответам испытуемых на последовательность вопросов, с различных сторон отражающих данный конструкт. Более того, ФА разрешает измерять не только прямо ненаблюдаемые (скрытые) переменные, но и оценивать определенные качества, каковые смогут намеренно прятаться и искажаться испытуемым при прямом их тестировании, но проявляться (т.е. быть измеренными) косвенно через разные связанные с ними качества, оцениваемые прямо.
На протяжении научного изучения ФА может выступать в двух ипостасях: как разведочный (эксплораторный) и как проверочный (конфирматорный) способ анализа данных. В первом случае ФА употребляется ex post factum, т.е. для анализа уже измеренных в эмпирическом изучении переменных и, практически, оказывает помощь исследователю их структурировать; на этом этапе совсем не обязательно делать априорные догадки о их связях и количестве факторов с наблюдавшимися переменными. Тут основное значение ФА — структурировать связи между переменными, оказать помощь сформулировать рабочие догадки (пускай время от времени и весьма умозрительные) о обстоятельствах найденных связей. В большинстве случаев, такое применение ФА характерно для начальной, ориентировочной стадии работы, в то время, когда очень многое неявное думается явным, непростое — несложным, и напротив. В отличие от разведочного, конфирматорный ФА употребляется на более поздних стадиях изучения, в то время, когда в рамках какой-либо теории либо модели сформулированы четкие догадки, связи между переменными и факторами достаточно выяснены, и исследователь их может прямо указать. Тогда конфирматорный ФА выступает как средство проверки соответствия сформулированной догадки взятым эмпирическим данным.
Обобщая вышесказанное, выделим главные цели применения ФА:
1. Понижение размерности числа применяемых переменных за счет их объяснения меньшим числом факторов. Обобщение взятых данных.
2. Группировка, компактная визуализация и структурирование взятых данных.
3. Опосредованное, косвенное оценивание изучаемых переменных при неосуществимости либо неудобства их прямого измерения.
4. Генерирование новых идей на этапе разведочного анализа. Оценка соответствия эмпирических данных применяемой теории на этапе ее подтверждения.