Процесс определения психофизической функции имеет несколько этапов:
1. Получение в процедуре измерения оценок стимулов, находящихся в заданном отношении к стандартным стимулам.
2. Проведение регрессионного анализа взятых данных, построение графика деления (умножения) на n и психофизической зависимости.
3. Проверка исполнения особенностей шкалы взаимоотношений.
4. Определение вида психофизической зависимости.
Разглядим последовательно любой из этих этапов на примере работы (Харпер, Стивенс, 1948) по взвешиванию грузов.
3. Организация измерительной процедуры.
При измерении оценок стимулов, находящихся в заданном к стандартным стимулам отношении, употребляется какой-либо из способов определения локализации точки на оси (способы границ, констант либо подравнивания). Процедуры этих способов минимизируют возможность систематических неточностей в оценке. Выбранный психофизический способ задает порядок предъявления переменных стимулов (Sc), среди которых необходимо выбрать находящийся в заданном отношении к стандартному, и метод вычисления средней оценки, потому, что постоянно имеет место разброс оценок, приобретаемых в отдельных пробах и у различных испытуемых.
Сравниваемые стимулы выбираются так, дабы охватить целый вероятный диапазон разброса оценок при подборе стимула, находящегося в заданном отношении к стандарту, и обеспечить хорошую точность оценки, т.е. они изменяются малыми шагами. Они предъявляются или рандомизированно (способ констант), или восходящими и нисходящими последовательностями (способ подравнивания). Средняя оценка вычисляется как точка субъективного равенства (PSE). Число измерений на каждую PSE возможно уменьшено при хорошей “кучности” оценок. В большинстве случаев их число лежит в пределах от 30 до 100 на точку.
Стандартные стимулы выбираются так, дабы охватить всю область измеряемого показателя, а их число должно быть таково, дабы обеспечить обнаружение разрывов психофизической функции, если они имеется, и проведение ровной кривой, в случае, если их нет. В большинстве случаев, употребляется не меньше 5 стандартных стимулов. В большинстве случаев величины стандартных стимулов выбираются так, дабы составить геометрический последовательность, потому, что психофизическая зависимость значительно чаще нелинейна.
Повторные оценки смогут быть взяты при опросе группы испытуемых, при повторном опросе одного испытуемого, и обоими этими методами в зависимости от того, желаем мы взять эту шкалу для одного испытуемого либо группы испытуемых. При повторном опросе одного испытуемого появляется вопрос, приобретать ли сходу пара оценок для одного стандартного стимула, а после этого переходить к следующему, либо же приобретать одну оценку каждого из стандартных стимулов, а после этого повторять всю серию. самоё предпочтительным с позиций независимости оценок есть второй метод, что, но, может оказаться более тяжёлым для испытуемого.
направляться учесть таковой фактор, как тренированность испытуемых. Тренировка может уменьшить разброс оценок, т.е. расширить их надежность, но вместе с тем процесс тренировки может поменять вид психофизической функции. Более того, разные методы тренировки смогут привести к разным трансформациям функции. Ответ, тренировать ли испытуемых, зависит от того, как будет употребляться выстроенная шкала. К примеру, в случае, если в будущем она будет использоваться в работе с нетренированными испытуемыми, то не нужно проводить их тренировки.
Предотвращение систематических смещений и ошибок, обусловленных внешними факторами.
Обстоятельства смещений смогут быть самыми разнообразными. Два отлично известных примера — фиксированный временной либо пространственный порядок предъявления переменного и стандартного стимулов ведет к появлению систематических смещений. Эти неточности смогут быть предотвращены при помощи уравновешивающих процедур, предусмотренных в классических пороговых способах.
Пара сложнее осуществлять контроль влияние так называемых контекстных эффектов. Многие изучения продемонстрировали, что в то время, когда испытуемому предъявляют последовательность переменных стимулов, он пробует выбрать как соответствующий заданному отношению со стандартом тот из стимулов, что расположен около середины последовательности. Данный факт отлично разъясняется теорией уровня адаптации Хелсона. Влияние комплекта стимулов на суждение особенно очень сильно в тех случаях, в то время, когда оценка затруднительна для испытуемого. Гарнер (1954) продемонстрировал, что выбор стимула, оцениваемого как добрая половина стандарта, абсолютно зависит от применяемого диапазона переменных стимулов. Гилфорд (1954) рекомендует для полного устранения этого результата применять один долгий последовательность переменных стимулов для всех стандартных. Эти Стивенса и Поултона (1956) подтверждают тот факт, что контекстные эффекты исчезают, в то время, когда испытуемого не ограничивают фиксированным рядом сравниваемых стимулов, к примеру, при применении процедуры подравнивания.
Ниже приводится последовательность стандартных стимулов весов, употреблявшихся в работе Харпера и Стивенса (1948) и соответствующие им медианы (Md) весов, оцененных испытуемыми как равные половине стандартных (табл. 1).
Таблица 1
Результаты оценки испытуемыми стимула как половины стандартного (по Харперу и Стивенсу, 1948)
 |
4. Построение графика деления (умножения) на nи психофизической функции.Средняя оценка стимулов, находящихся в заданном отношении n со стандартом, вычисляется или как медиана Md, которая есть неотёсанной, но легко вычисляемой оценкой, или как среднее геометрическое G, определяемое по формуле:
(1)
где, S1… Sn— величины стимулов, оцененных как составляющие заданную часть от стандартного; n — число повторных оценок .
В случае, если число оценок больше трех, то G эргономичнее обнаружить методом логарифмирования:
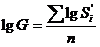 |
. (2)
Харпер и Стивенс воспользовались, как уже было сообщено выше, медианой для оценки весов, принимаемых как добрая половина стандартного. На основании взятых данных была найдена зависимость S’= f(Sst), где S’– медиана стимулов, оцениваемых как добрая половина стандартного стимула. Эта зависимость представлена на рис. 1.
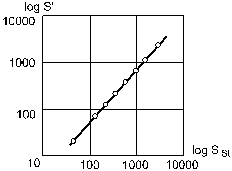 |
Рис. 1. График “деления на 2”: по оси абсцисс – веса стандартного стимула (Sst), в граммах; по оси ординат – веса, принимаемые как добрая половина от стандартных (S’), в граммах. Обе оси забраны в логарифмическом масштабе из-за громадного диапазона значений стимулов. По экспериментальным точкам совершена регрессионная прямая (по Харперу и Стивенсу, 1948)
В этом случае экспериментальные точки практически совершенно верно ложатся на прямую, и она без явных неточностей возможно совершена на глазок.
В большинстве случаев линия, сопоставляющая на графике деления на n каждому стандартному стимулу не S’, принимаемый как объективно в n раз меньший, проводится через конечное и, в большинстве случаев, маленькое число точек, соответствующих использованным стандартным стимулам. Проведение плавной линии через пара точек, очевидно, постоянно содержит неточность, неточность. Но, в случае, если вид зависимости известен (линейная, логарифмическая и т.п.), то неточность по отношению к экспериментальным точкам возможно минимизировать. Минимизация неточности есть задачей регрессионного анализа, а полученная в следствии ответа данной задачи линия именуется линией регрессии (прямолинейной, логарифмической и т.п.). До тех пор пока мы можем забыть о допускаемой неточности в определении данной кривой и разглядывать ее как постоянную и “правильную” для всех S.
Как от графика деления на n, что есть лишь стимульно-стимульной функцией, перейти к психофизической функции? Для этого необходимо лишь ввести единицу измерения на субъективной шкале, потому, что все необходимые для построения субъективной шкалы соотношения субъективных и стимульных значений уже находятся в взятой в опыте зависимости: S’ = f(Sst). Для этого выбирается какой-либо из стандартных стимулов и соответствующее ему значение на шкале ощущения (Z) принимается за единицу (Z=1). Харпер и Стивенс выбрали в качестве такового чувство тяжести, появляющееся при поднятии груза 100 г., и назвали эту единицу “вег” (от старонорвежского слова, имеющего значение “поднимать”). Конечно, что шкальное значение того веса, что испытуемый оценил как в два раза менее тяжелый, чем Sst= 100 г, равняется 1/2 вега. Это вес 77 г. В принципе способ установления заданного отношения разрешает указать любой стимул, которому соответствует шкальное значение, равное na, где а = 0, ±1, ±2 …. В отечественном примере, где 1/n = 1/2, возможно определить значения 1/4, 1/8, 1/16, 2, 4, 8, 16 и т.д. Как это делается, продемонстрировано на рис. 2.
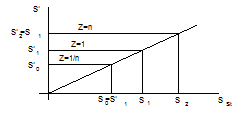 |
Рис. 2. Пример построения психофизической функции: по оси абсцисс – вес стандартного стимула, в граммах; по оси ординат – шкальные значения тяжести (Z).
Примем, что шкальное значение, соответствующее стимулу S1, равняется 1. Так, мы вводим единицу измерения на будущей шкале (в отечественном примере — это 1 “вег”) и строим на ней первую точку с координатами (100; 1 либо S1; S’1 на рис. 2). Тогда стимулу S0, оцененному как в n раз меньший, соответствует шкальное значение 1/n. Отложив по оси абсцисс значение S0 (мы его находим легко из графика “деления на n”, приведенного на рис.1, т.к. в опыте уже отыскан тот вес, что ощущается как добрая половина от S1), соотносим его со шкальным значением 1/n и строим на графике вторую точку. В отечественном примере шкальное значение S’0 будет равняется 1/2. Так возможно отыскать и все предстоящие отрицательные степени n. Конечно, что точность построения психофизической функции будет зависеть от точности вычислений стимульных значений по графику “деления на n”, что, со своей стороны, определяется “хорошестью” подгонки экспериментальных точек под плавную кривую либо прямую, отражающую устойчивость взятой эмпирической зависимости. Чтобы получить все хорошие степени того же отношения, нужно поменять направление отечественных расчетов. Отыщем по графику “деления на n” величину стимула, что при делении на n дает 1 вег — S’2. Эту величину возможно отыскать, совершив перпендикуляр от той точки на оси ординат, которая соответствует 1 вегу, до пресечения с аппроксимирующей кривой (прямой), и из точки пересечения опустить перпендикуляр на абсциссу. Отысканная величина (S2) соответствует n вегам (в отечественном примере n = 2) и может, со своей стороны, быть использована для определения 2n вегов и т.д.
По отысканным парам значений на субъективной шкале (Z) и на физической шкале стимулов (S) строится психофизическая функция: по оси абсцисс откладываются субъективные размеры (к примеру, веги), а по оси ординат — соответствующие им значения физического параметра стимула (к примеру, граммы). Плавная линия, соединяющая точки, образованные парами значений Z и S, и образует графическую шкалу ощущений тяжести. Эта линия возможно совершена “на глазок” либо с применением способов регрессионного анализа и аппроксимирована подходящей математической функцией.
В будущем психофизическая зависимость может употребляться для определения шкальных значений любого стимула, среди них и для того чтобы, что не используется в опыте, к примеру, лежащего между S’1и S’2. В действительности, такому стимулу нельзя приписать конкретно шкальное значение, потому, что к нему нельзя “прийти” от предъявлявшихся в опыте стимулов S1либо S2методом обрисованной выше процедуры посредством кривой “деления на n”. Возможно лишь утверждать, что его шкальное значение лежит между 1/n и 1. Это утверждение будет справедливо только при допущении, что психофизическая зависимость есть строго монотонной. Неточность в определении шкального значения, соответствующего этому стимулу, возрастает за счет неточности при построении психофизической зависимости.
Психофизическая функция, выстроенная согласно данным Харпера и Стивенса, продемонстрирована на рис. 3.
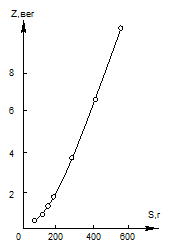 |
Аналитический метод, что дает более правильное определение субъективной шкалы, потому, что лишен неточностей, которые связаны с неточностью проведения графических работ, детально обрисован Гилфордом (1954). Тут приведем лишь краткую схему аналитического ответа, потому, что для тех, кто обладает минимальными навыками регрессионного анализа, посредством любой современной статистической программы оно не воображает громадного труда. Подобранные в опыте значения стимулов, оцененных как в n раз меньшие (громадные), чем стандартные, преобразуются в логарифмы и посредством способа мельчайших квадратов определяется уравнение прямой. Уровень качества подгонки взятой прямой под экспериментальные точки оценивается стандартным образом. Применяя это уравнение, возможно вычислить любое значение на оси “X” по известному значению на оси “Y” (и напротив). Конечно, что точность приобретаемых оценок будет зависеть от качества взятой регрессионной прямой. Находя так необходимые значения на оси “X” конструируемой психофизической функции, приобретают все нужные точки. Затем, используя способы регрессионного анализа, определяют вид функции, обрисовывающей психофизическую зависимость. Потому, что психофизические функции, в большинстве случаев, нелинейны, эргономичнее воображать результаты на графике и проводить регрессионный анализ в логарифмическом масштабе по оси абсцисс. В случае, если эта функция подчиняется закону Фехнера, то в этом случае она будет прямой. В случае, если же психофизическая функция степенная, то представление ее в виде прямой возможно взять лишь в двойных логарифмических координатах (так именуемые log-log-координаты), т.е. введя логарифмический масштаб кроме этого и по оси ординат. Так, изображение психофизической функции в виде прямой в логарифмических координатах, есть необычным “тестом” на ее соответствие одному из фундаментальных психофизических законов.
5. Проверка соответствия процедуры шкалирования шкале взаимоотношений: деление (умножение) на два взаимно несложных числа.
Если судить по вышеприведенному описанию, способ фракционирования достаточно неотёсан с позиций получения правильной психофизической зависимости. Оказывается, но, что это не единственный а также не самый главный его недочёт. Дело в том, что процедура этого способа не содержит возможности проверить, существует ли соответствие между выполненными испытуемым операциями отыскания стимула, относящегося как 1/n к стандартному, и особенностями шкалы взаимоотношений. Следовательно, мы имеем предлог сомневаться в том, вправду ли возможно строить шкалу взаимоотношений по кривой деления (умножения) на n.
Проверка исполнения особенностей шкалы взаимоотношений. Уточним, что направляться осознавать под “соответствием операций особенностям шкалы”. В этом случае соответствие свидетельствует, что операция деления (умножения) стимула на число n (т.е. отыскания стимула, составляющего субъективно 1/n-ю от стандарта) эквивалентна математической операции деления (умножения) наименованного числа (значения предполагаемой шкалы) на число-скаляр n. “Эквивалентна” свидетельствует, что она владеет теми же особенностями. Названная математическая операция владеет особенностями ассоциативности, коммуникативности, тотальной сравнимости, неизменности и обратимости при умножении на 1. Для отечественных целей достаточно представить эти свойства в виде следующих правил:
1. Z = Z · 1 для любого шкального значения Z.
2. Z · a1· a2· a3 … · ?n = Z · b1· b2· b3… · bn,
в случае, если и лишь в случае, если a1· a2· a3 … · an = b1· b2· b3… · bn(это правило включает в себя и коммуникативность, и ассоциативность).
3. Для любых двух Z1и Z2существует единственное ?, такое, что Z1= Z2· a (тотальная сравнимость).
4. В случае, если Z1= Z2· a, то Z2= Z1· 1/a (это свойство обратимости)1.
Разглядим, что означают эти правила на языке эмпирических операций деления (умножения):
1. Свойство 1 выполняется разумеется в любой момент, в случае, если лишь нет систематических неточностей, которые связаны с условиями опыта.
2. Пускай испытуемый “дробит” стимул S на 2, тем самым он выбирает новый стимул S’1. Стимул S’1он “дробит” на 3 — выбирает стимул S’2. Если бы первое “деление” было не на 2, а на 3, то вместо S’1должен был бы выбираться некий стимул S»1. Правило 2 гарантирует, что в случае, если сейчас S»1“поделить” на 2, то окажется снова S’2(т.к. 1/3 · 1/2 = 1/2 · 1/3). Данный пример, и и другие примеры, демонстрирующие диагностику правила 2, приведены на рис. 4.
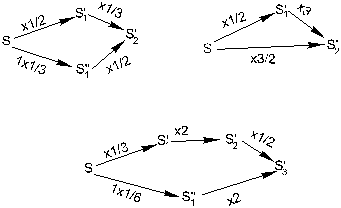 |
Рис. 4. Пример, демонстрирующий исполнение правила 2
3. Правило 3 свидетельствует, что методом каких-то “делений” и “умножений” от одного стимула в любой момент возможно “добраться” до любого другого. В случае, если опыт организован так, что это правило выполняется, то мы избавляемся от необходимости строить психофизическую зависимость примерно (так как до любого стимула возможно “добраться” от “единичного” и тем самым взять совершенно верно соответствующее ему шкальное значение).
Возможно доказать следующее утверждение: в случае, если экспериментально выстроены не одна кривая “деления на n” (см. рис. 1), а две — “деления на m” и “деления на n”, где n и m — взаимно простые числа (к примеру, 2 и 3), то правило 3 выполняется. Подтверждение направляться из того факта, что любое шкальное значение возможно какое количество угодно совершенно верно приближено числом вида 2a· 3bа,b = 0, ±1, ±2,…).
4. Правило 4 поясняется на рис. 5.
xa
X1/a
Рис. 5. Пример, демонстрирующий исполнение правила 4
Тут, как и на рис. 4, стрелка обозначает выбор нового стимула. Проверка выполнимости правила возможно осуществлена так: строится кривая “деления на n” и кривая “умножения на n”, они должны совпасть с точностью до перемены осей (как функции ln и exp).
6. Определение вида психофизической зависимости.
Если бы вероятный вид зависимости был совсем малоизвестен, было нужно бы проделывать громадную работу: совершить регрессионный анализ для умелых данных, проверить исполнение особенностей шкалы взаимоотношений, выстроить кривую психофизической зависимости и лишь затем возможно подбирать математическое выражение для взятой психофизической функции. Положение облегчается, в случае, если вид психофизической зависимости известен либо по крайней мере должен быть осуществлен выбор между несколькими известными видами.
Как мы знаем, что большая часть психофизических зависимостей возможно представлено в степенной либо логарифмической форме. Разглядим главные варианты этих те следствия и форм, каковые из них вытекают для умножения “и” кривых “деления”. Все эти следствия (не смотря на то, что это и не будет доказываться) в действительности являются не только нужными, но и достаточными условиями исполнения соответствующих форм психофизической зависимости.
1. Несложная степенная форма Z = aSa. Какой вид должна иметь кривая “умножения” на n? Дабы узнать это, разглядим два значения стимула S и Sn, такие, что соответствующие им ощущения относятся как Z и Z · n:
Z = aSa, (3)
Zn= aSan. (4)
Поделим равенство (4) на (3):
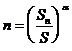 (5)
(5)
Так, в случае, если выстроить прямую наилучшего приближения согласно данным “умножения на n” (стимульно-стимульная кривая, где по оси абсцисс отложены значения стандартного стимула S, а по оси ординат — стимула, субъективно в n раз большего S’, см. рис. 6), то:
1) прямая пройдет через начало координат (0,0);
2) наклон прямой продемонстрирует показатель степени в законе Стивенса. Данный показатель мы возьмём, в случае, если заберём логарифм тангенса наклона (при основании, равном коэффициенту “умножения/деления” n), т.е. logntgj, и вычислим обратную этому выражению величину (см. рис. 6).
2. Степенная форма Z = k(S — S0)aявляется степенной зависимостью с “порогом” (при S = S0чувство равняется 0, т.е. исчезает). Значения S
Z = k(S — S0) a, (3′)
Zn = k(Sn- S0) a. (4′)
Поделив второе равенство на первое и совершив элементарные преобразования, возьмём:
Sn= n1/a S + (1 — n1/a)S0. (5′)
Итак, линия “умножения на n” оказывается прямой с наклоном n, но не проходит через начало координат (см. рис. 7).
 |
Рис. 6. Вид функции умножение на n, проходящей через начало координат: по оси абсцисс — величина стандартного стимула; по оси ординат — величина стимула, оцененного в n раза больше, чем обычный
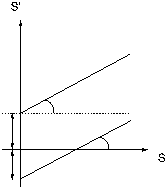 |
Рис. 7 . Вид функции умножение на n, смещенной по оси ординат и не проходящей через начало координат: по оси абсцисс — величина стандартного стимула; по оси ординат — величина стимула; оцененного в n раза больше, чем обычный
Выстроив прямую наилучшего приближения согласно данным “умножения на n”, вычислим подобно тому, как это делалось в прошлом пункте, показатель степени Стивенса. Но, непрохождение прямой через (0,0) не разрешает ограничиться проделанным: слишком мало знать лишь a, необходимо еще вычислить S0. Прямая “умножения на n” пересекает ось ординат на уровне (1 -n1/a)S0. Поделив эту величину на (1 -n1/a), возьмём S0.
На рис. 6 и 7 изображена прямая “умножения на n” в предположении, что Z = aSa(рис. 6) и в предположении, что Z = k(Sn- S0)?a?(рис. 7). На рис. 7 кроме этого продемонстрирован случай, в то время, когда (1 -n1/a)S0— величина отрицательная. В случае, если S0вправду есть “порогом”, то независимо от символа данной величины S0должна быть величиной хорошей. В случае, если этого не случится, то интерпретация S0изменяется. Функция Z = k(S+r)a(где r0) показывает наличие “шума”, так что и при нулевом стимуле S0имеет место ненулевое чувство Z = kr a. Эта отличие в интерпретации не воздействует на формальный анализ.
3. Несложная логарифмическая зависимость Z = logS. В этом случае пара равенств, задающих кривую “умножения на n” такова:
Z = logS ,(3′)
Zn= logSn . (4′)
Разумеется, что, совершив те же вычисления, как и в прошлых пунктах, мы возьмём:
logSn= nlogS, (5′)
т.е. определенно нелинейную зависимость. Значит, в случае, если мы ожидаем логарифмическую, а не степенную зависимость, не нужно строить прямых наилучшего приближения. В случае, если мы все же их выстроим, то они окажутся “нехорошими” в смысле приближения к умелым точкам, и самое основное, вычисления по различным n (n=1/2, 1/3 и 2) дадут нам различные размеры a. Выход из затруднения пребывает в том, что эти “умножения на n” направляться откладывать в двойных логарифмических координатах. Тогда, в соответствии с (2’’), наилучшим приближением будет прямая, наклон которой равен коэффициенту фракционирования n (см. рис. 8).
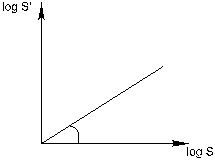 |
Рис. 8. Вид функции умножение на n, проходящей через начало координат в двойных логарифмических координатах:
по оси абсцисс — логарифм стандартного стимула; по оси ординат — логарифм величины стимула, оцененного в n раза больше, чем обычный
4. Логарифмическая форма Z = logS + b. В этом случае имеем:
Z = logS + b, (3»)
Zn = logSn+ b. (4»)
Поделив второе равенство на первое и произведя элементарные преобразования, возьмём:
logSn= nlogS + (n-1)b. (5»)
График данной зависимости в двойных логарифмических координатах продемонстрирован на рис. 9.
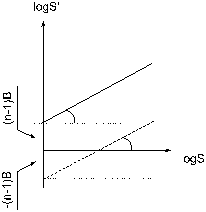 |
Рис. 9. Вид функции умножение на n, смещенной по оси ординат и не проходящей через начало координат, в двойных логарифмических координатах: по оси абсцисс — логарифм стандартного стимула; по оси ординат — логарифм величины стимула, оцененного в n раза больше, чем обычный; штриховой линией продемонстрирован случай, в то время, когда (n-1)b — величина отрицательная
§ 2. Способ оценки величины
Способ оценки величины имеет своим предшественником способ дополнительного стимула, созданный Меркелем еще в 1890 г., но позже прочно забытый. В современной форме способ оценки величины предложен С. Стивенсом. Он утвержает, что “… все началось с дружеского спора с сотрудником, что сообщил: “Вы вычисляете, что у каждой громкости имеется собственный число и что, в случае, если кто-то издаст стон, то я смогу сказать ему число, соответствующее этому стону”. “Мысль стоит того, чтобы ее испробовать”, — ответил я. Мы дали согласие, что как и в любой проблеме измерений сперва необходимо решить вопрос о размере отечественных единиц. Я сказал громкий звук, обозначив его громкость как 100. После этого я предъявил последовательность разных интенсивностей в случайном порядке и с готовностью, поразившей нас обоих, мой знакомый пронумеровал звуки в абсолютно сходной манере”. Создавая данный способ, Стивенс стремился максимально снять каждые ограничения испытуемого в выражении собственных впечатлений числом, ограничения, которые связаны с введением обозначений финишей стимульного последовательности либо с необходимостью определения взаимоотношений к заданному стандарту. Он желал уменьшить какую бы то ни было предрасположенность испытуемого отвечать в некотором роде в силу выбранной экспериментатором совокупности ответных реакций, к примеру, отвечать лишь дробями.
Итак, главное допущение прямого шкалирования пребывает в утверждении, что человек способен охарактеризовать числом величину любого собственного впечатления, будь то приятность вкуса либо громкость звука, красота произведения искусства либо видимая яркость. Не смотря на то, что прямое шкалирование используется по большей части в тех случаях, в то время, когда известен соответствующий измеряемый ощущениями физический континуум стимулов, согласно точки зрения Стивенса нет никаких принципиальных ограничений для прямого шкалирования и в тех случаях, в то время, когда исследователя интересует не психофизический закон.
Для получения шкалы способом оценки величины испытуемому должен быть предъявлен фиксированный последовательность надпороговых стимулов, охватывающий достаточно широкий диапазон измеряемого показателя. По утверждению Стивенса, средний испытуемый в оптимальных условиях способен оценить ощущения по шкале от 1 до 1000, вызванные стимулами, физическая интенсивность которых изменяется от 1 до биллиона (диапазон в 90 дБ). В большинстве случаев, в измерениях участвует довольно много испытуемых (n ?15), но любой дает мало оценок на любой стимул (в большинстве случаев всего 2). Стимулы предъявляются в случайном порядке. Частенько различным испытуемым предъявляются разные случайные последовательности стимулов. Воздействие временных факторов балансируется при получении второй оценки предъявлением стимульной последовательности в обратном порядке.
Существуют 2 формы способа оценки величины: с заданным модулем либо со свободным модулем (в противном случае его именуют без модуля).
1. Способ оценок величины с заданным модулем.
В начале опыта испытуемому предъявляется обычный стимул и сообщается соответствующее позванному им ощущению некое числовое значение на субъективной шкале показателя — модуль. Все другие оценки испытуемый обязан соотносить с этим модулем. Задача испытуемого детально описывается в инструкции. Как пример забрана инструкция из работы Энгена (1971) по шкалированию запахов:
“Мы желаем, дабы Вы выяснили интенсивность запахов. Данный стимул воображает стандартную интенсивность. Другие запахи будут предъявляться в нерегулярном порядке. Все они приблизительно однообразны по качеству, но их интенсивность разна. Назовем обычный запах “10”. Ваша задача содержится в оценке интенсивности либо силы всех других запахов довольно стандартного. Иначе говоря в случае, если стандарт обозначен 10, как Вы обозначите сравниваемый запах? Применяйте каждые числа, каковые кажутся Вам подходящими — дроби либо целые. К примеру, в случае, если сравниваемый стимул пахнет в 7 раз посильнее стандартного, обозначьте его 70. Если он образовывает 1/5 силы стандартного, оцените его 2, в случае, если 1/20, обозначьте 0.5 и т.д.