Новейшие технологии и
Формы логико-обучения детей и математического развития дошкольного возраста
УЧИТЕЛЬ
Е.В.СЕМЁНОВА
ВОПРОСЫ К ТЕМЕ:
«Новейшие технологии ЛОГИКО-Обучения ДЕТЕЙ и МАТЕМАТИЧЕСКОГО Развития ДОШКОЛЬНОГО ВОЗРАСТА»
1. Исходя из сути и характерных линия проблемно-игровой технологии, выясните, в чём состоит её значение для математического развития детей?
2. Какие конкретно средства включает проблемно-игровая разработка обучения дошкольников математике?
3. В чём особенность логико-математических игр? умения и Какие знания дети осваивают с их помощью?
4. Какие конкретно приёмы употребляются для проблемных обстановок в ходе овладения детьми логико-опытом и математическим содержанием?
5. Каков метод применения проблемных обстановок в обучении дошкольников математике?
6. В чём сущность логико-математических занятий и сюжетных игр?
7. В чём исследования и отличие экспериментирования от проблемного обучения?
8. Раскройте этапы управления независимой исследовательской деятельностью дошкольников.
9. Приведите примеры игр, упражнений, заданий математического содержания для организации экспериментирования в различных возрастных группах.
10. В чём специфика творческих задач, вопросов, обстановок как приёма обогащения логико-математического опыта дошкольников?
11. Подберите наглядный материал для организации игры «Логический поезд». Совершите игру в группе студентов.
Новейшие технологии ЛОГИКО-Обучения ДЕТЕЙ и МАТЕМАТИЧЕСКОГО Развития ДОШКОЛЬНОГО ВОЗРАСТА
выбор и Разработка разработок логико-математического развития детей зависит от того, что подлежит освоению, и от направления развития интеллектуальной деятельности ребёнка.
В дошкольном возрасте ребёнок осваивает математические понятия, зависимости и связи, методы действий; обучается выбирать активные поисковые действия, осуществлять деятельность на базе логических операций мышления, соотносить действия с результатом, стремиться к цели на базе прогнозирования, объективно оценивать итог.
В обучении дошкольников математике применяют проблемно-игровую разработку, включающую следующие средства:
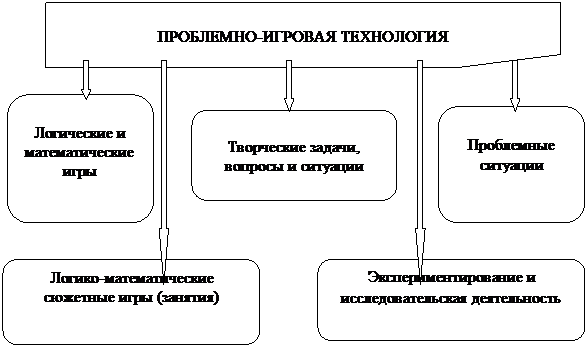
Сущность разработке – создание взрослыми обстановок, в которых ребёнок пытается к активной деятельности и приобретает хороший творческий итог.
Характерные черты разработки:
1. ребёнок не ограничен в поиске практических действий, экспериментировании, общении для противоречий и разрешения ошибок, проявлении огорчений и радости;
2. в большинстве случаев исключаются подробное объяснение и показ;
3. ребёнок самостоятельно находит метод достижения цели либо осваивает его;
4. ребёнок конечно принимает помощь со стороны взрослого: частичную подсказку, участие в исполнении либо уточнении действий, речевых способов оценки и т.д.;
5. взрослый создаёт мотивацию и подбирает занимательные для ребёнка игры, упражнения, развивающие сообразительность и смекалку.
Логические и математические игры.
Современные логические и математические игры разнообразны. В них ребёнок осваивает эталоны, модели, обращение, овладевает методами познания, начинается мышление.
- настольно-печатные: «форма и Цвет», «Сосчитай», «Игровой квадрат», «Прозрачный квадрат», «Логический поезд» и др.
- игры на объёмное моделирование: «Кубики для всех», «Тетрис», «Шар», «Змейка», «Ёж», «Геометрический конструктор» и др.
- игры на плоскостное моделирование: «Танграм», «Сфинкс», «Т-игра» и др.
- игры из серии «цвет и Форма»: «Сложи узор», «Уникуб», «Цветное панно», «Многоцветные квадраты», «Треугольное домино», «Дабы цвет не повторялся» и др.
- игры на составление целого из частей: «Дроби», «Сложи квадрат», «Греческий крест», «Сложи кольцо», «Шахматная доска» и др.
- игры-забавы: лабиринты, перестановки («Ханойская башня», «Чайный сервиз», «бараны и Козлы», «Упрямый осёл»);
- головоломки (пазлы, мозаики, «Радуга», «Фея цветов», «Бабочки», «Рыбки», «Умный клоун», «Петрушка», математические головоломки – волшебные квадраты; головоломки с палочками) и др.
Проблемные обстановки.
Это средство овладения поисковыми действиями, умением формулировать личные мысли о методах поиска и предполагаемом результате, средство развития творческих свойств.
Структурными компонентами проблемной обстановке являются:
- проблемные вопросы (какое количество методами возможно разрезать квадрат на 4 части?),
- занимательные вопросы (У стола четыре угла. Сколько будет у стола углов, в случае, если один отпилить? какое количество месяцев в году содержат 30 дней?),
- занимательные задачи (какое количество финишей у трех палок? А у трех с половиной? Коля поспорил, что выяснит, какой будет счет в игре футбольных команд «Спартак» и «Динамо» перед матчем , и победил спор. Какой был счет?),
- задачи-шутки (Выше какого именно забора ты можешь прыгнуть? Яйцо пролетело три метра и не разбилось. По какой причине?).
Сперва взрослый ставит перед детьми проблему, получает её осмысления, направляет внимание детей на необходимость её решения. После этого идёт их проверка и выдвижение гипотез практическим путём, коллективное обсуждение путей и ситуации её решения. К примеру: «На столе лежат три карандаша различной длины. Как удалить из середины самый долгий карандаш, не трогая его?», «Как посредством одной палочки выложить на столе треугольник?».
Логико-математические сюжетные игры (занятия).
Это игры, в которых дети обучаются выявлять и абстрагировать свойства, осваивают операции сравнения, обобщения и классификации. Для них характерно наличие сюжета, действующих лиц, схематизации. Таковой комплекс игр предложен Е.А.Носовой на базе блоков Дьенеша: Мышки – норушки. Запасы на зиму. Автомобильная трасса. Выращивание дерева. Где чей гараж? Научи Незнайку. Загадки без слов. Переводчики. Выстрой цепочку. Две дорожки. У кого в гостях Винни-Пятачок и Пух? Фабрика. Архитекторы. Помоги фигурам выбраться из леса. Оформим витрину. Выстрой дом. Подели блоки – 1. блоки – 2. Помоги игрушке. Подели блоки – 3. Подарки для трех поросят. И др.