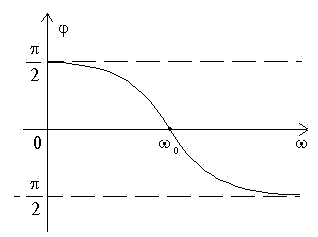
Комплексная передаточная функция
Передаточная функция — один из способов математического описания динамической совокупности. Употребляется по большей части в теории управления, связи, цифровой обработке сигналов. Представляет собой дифференциальный оператор, высказывающий связь между выходом и входом линейной стационарной совокупности. Зная входной сигнал совокупности и передаточную функцию, возможно вернуть выходной сигнал.
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее действие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
Различают четыре вида передаточных функций:
1) передаточная функция по напряжению:
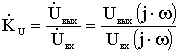
2) передаточная функция по току:
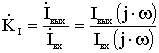
3) передаточное сопротивление:
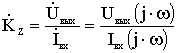
4) передаточная проводимость:
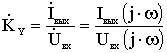
В общем виде передаточная функция:
представляется в виде АЧХ — К(?) и ФЧХ — ?(?)
Частотные характеристики
В случае, если на вход объекта подавать периодический сигнал заданной частоты и амплитуды, то на выходе будет кроме этого периодический сигнал той же частоты, но в общем случае второй амплитуды со сдвигом по фазе. Связь между параметрами периодических сигналов на выходе и входе объекта определяют частотные характеристики. Значительно чаще их применяют для описания направляться совокупностей:
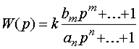 , n = m. , n = m. |
(2.40) |
Формально обобщенная частотная черта возможно взята из передаточной функциизаменой p на
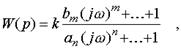
|
(2.41) |
и представлена в виде
| . | (2.42) |
Составляющие обобщенной частотной чёрта имеют следующие названия и самостоятельное значение:
- вещественная частотная черта (ВЧХ),
- мнимая частотная черта (МЧХ),
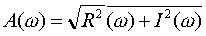 амплитудная частотная черта (АЧХ),
амплитудная частотная черта (АЧХ),- фазовая частотная черта (ФЧХ).
Частотная черта по выражению (2.42) возможно выстроена на комплексной плоскости. В этом случае финиш вектора, соответствующий комплексному числу , при трансформации от 0 до прочерчивает на комплексной плоскости кривую, которая именуется амплитудно-фазовой чёртом (АФХ).
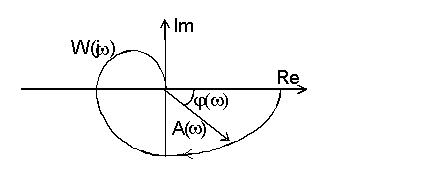
Пример амплитудно-фазовой чёрта совокупности
Фазо-частотная черта (ФЧХ) — графическое отображение зависимости сдвига по фазе между входным и выходным сигналами в зависимости от частоты,
Для определения знаменатель и числитель W(j ) разлагаются на множители не выше второго порядка
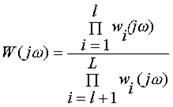 ,
,
тогда 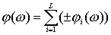 , где символ + относится к i=1,2,…,l (числителю передаточной фунции), символ — -к i=l+1,…,L(знаменателя передаточной функции).
, где символ + относится к i=1,2,…,l (числителю передаточной фунции), символ — -к i=l+1,…,L(знаменателя передаточной функции).
Каждое из слагаемых определяется выражением
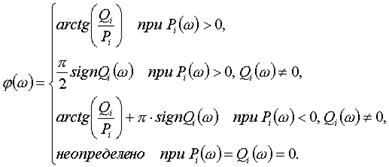
где .
Амплитудно-частотная черта (АЧХ) — функция, показывающая зависимость модуля некоей комплекснозначной функции от частоты. Кроме этого может рассматриваться АЧХ вторых комплекснозначных функций частоты, к примеру, спектральной плотности мощности сигнала.
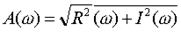
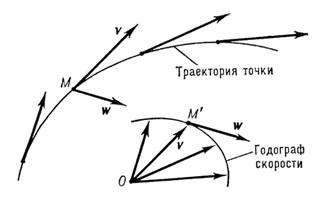
Годограф — кривая, воображающая собой геометрическое место финишей переменного (изменяющегося со временем) вектора, значения которого в различные моменты времени отложены от общего начала
Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого трансформации, имеющей направление касательной к годографу.
К примеру, скорость точки есть величиной, изображаемой переменным вектором v. Отложив значения, каковые имеет вектор v в различные моменты времени, от начала О, возьмём годограф скорости; наряду с этим величина, характеризующая быстроту трансформации скорости в точке М, другими словами ускорение (в данной точке), имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке М’.
Частотные характеристики двухполюсников
четырехполюсники и Пассивные двухполюсники включают комплект резистивных и реактивных (индуктивных и емкостных) элементов, в которых протекают электрические токи под действием какого-либо одного внешнего источника энергии. Для описания физических явлений в таких цепях при действии на входных зажимах источника гармонических колебаний с фиксированной частотой =const применяют способ комплексных амплитуд, что со своей стороны основывается на введении понятий комплексных сопротивлений либо проводимостей отдельных элементов цепи -r, 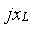 , , и комплексных амплитуд токов и напряжений – , .
, , и комплексных амплитуд токов и напряжений – , .
В общем случае у источника гармонических колебаний может изменяться не только начальная фаза и амплитуда, но и угловая частота — . Тогда комплексная черта источника (входного действия) записывается в виде функции мнимой комплексной переменной — ( ). Эту чёрта в большинстве случаев записывают в показательной (полярной) форме и именуют комплексной спектральной плотностью. Модуль данной характеристики именуют спектральной плотностью, а довод — фазовой плотностью либо фазочастотной чёртом. Так для напряжения имеем:
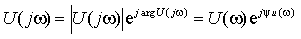
|
где — спектральная плотность напряжения, — фазовая плотность напряжения.
Подобно гармонический ток с переменной угловой частотой ? характеризуется собственной комплексной спектральной плотностью:
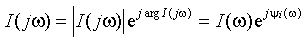
|
В зависимости от вида входного действия (электрического сигнала) спектральные плотности смогут иметь постоянный либо дискретный темперамент. В будущем для краткости будем опускать написание зависимости от угловой частоты, полагая , , , .
На рисeyrt изображен двухполюсник, имеющий два входных зажима, к каким подсоединяется источник входного сигнала. В случае, если к цепи присоединяется источник тока J(t), то входной ток i(t) = J(t), т.е. будет свободной функцией времени, а напряжение u(t) на входе определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют тока комплексов и отношение напряжения.
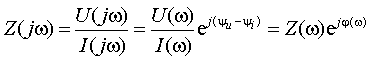
|
(*) |
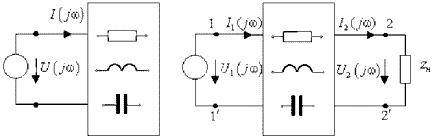
Такое отношение именуют комплексным входным сопротивлением
двухполюсника:
Из определения (*) направляться, что Z(j?) со своей стороны включает две характеристики: — амплитудно-частотную чёрта (АЧХ) и — фазочастотную чёрта (ФЧХ) функции входного сопротивления.
В случае, если к цепи присоединяется источник напряжения e(t), то напряжение на двухполюснике u(t) = e(t), т.е. будет свободной функцией времени, a ток i(t) определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение тока к напряжению, которое именуют комплексной входной проводимостью двухполюсника:
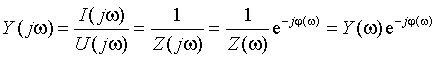
|
где Y(?) и ?(?) именуют соответственно АЧХ и ФЧХ функции входной проводимости.
52.Колебательный контур — осциллятор, воображающий собой электрическую цепь, содержащую соединённые конденсатор и катушку индуктивности. В таковой цепи смогут возбуждаться колебания тока (и напряжения).
Последовательный колебательный контур.
Разглядим цепь, складывающуюся из последовательно включенных катушки конденсатора и индуктивности. При действии на такую цепь переменного (гармонического) напряжения, через конденсатор и катушку будет протекать переменный ток, величина (амплитуда) которого возможно вычислена в соответствии с закону Ома: I = U/|Х?| , где |Х?| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора
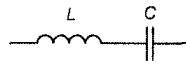
В случае, если соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Данный эффект именуется резонансом колебательного контура, сама схема из индуктивности и конденсатора — последовательным колебательным контуром, а частота, на которой проявляется данный эффект — частотой резонанса.
Добротность
Добро?тность — черта колебательной совокупности, определяющая полосу резонанса и показывающая, во какое количество раз запасы энергии в совокупности больше, чем утраты энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в совокупности. Другими словами, чем выше добротность колебательной совокупности, тем меньше утраты энергии за любой период и тем медленнее затухают колебания. Неспециализированная формула для добротности любой колебательной совокупности: 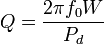
Коэффициент мощности
Коэффицие?нт мо?щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с позиций наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, как сдвигается по фазе переменный ток, протекающий через нагрузку, довольно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига.
Коэффициент передачи по напряжению
Коэффициент передачи (кроме этого коэффициент преобразования) — отношение напряжения на выходе той либо другой совокупности, предназначенной для передачи электрических сигналов, к напряжению на входе. В частном случае, в то время, когда входного сигнала и значения выходного являются однородными, коэффициент передачи именуют коэффициентом усиления. KП = UВЫХ / UВХ. Коэффициент передачи довольно часто высказывают в логарифмическом виде, как 20 lg (UВЫХ / UВХ), дБ.
В усилительных устройствах коэффициент передачи больше единицы (больше нуля в логарифмическом масштабе) именуют коэффициентом усиления (не путать с коэффициентом усиления антенны).
При рассмотрении пассивных устройств, и линий передачи, в то время, когда выходное напряжение меньше входного, употребляют понятие ослабление сигнала.
Амплитудно-частотные характеристики
График АЧХ для последовательного контура приведён на рис. Из графика видно, что графики АЧХ для C и L пересекаются при резонансной частоте
w= 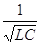
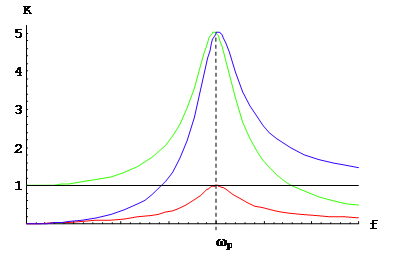
Фазо-частотные характеристики
Графики ФЧХ выглядят следующим образом 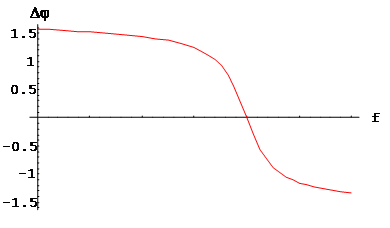
53. Последовательный колебательный контур.
Разглядим цепь, складывающуюся из последовательно включенных катушки конденсатора и индуктивности. При действии на такую цепь переменного (гармонического) напряжения, через конденсатор и катушку будет протекать переменный ток, величина (амплитуда) которого возможно вычислена в соответствии с закону Ома: I = U/|Х?| , где |Х?| -модуль суммы реактивных сопротивлений последовательно включенных катушки и конденсатора 
полоса и Избирательность пропускания
Избирательностью именуют свойство колебательного контура выделять колебания одной избранной частоты. Разные контуры владеют неодинаковой избирательностью. Дело в том, что в случае, если на контур воздействуют два сигнала, частоты которых близки, то он может оказаться не в состоянии поделить эти сигналы. Не нужно думать, что колебательный контур увеличивает напряжение либо ток лишь при правильного совпадения его частоты с собственной частотой колебательного контура. В случае, если частота источника, подключенного к контуру, незначительно отличается от резонансной частоты, то напряжение либо ток этого источника все же будут увеличены контуром, не смотря на то, что и в меньшей степени, чем при резонансе. Исходя из этого каждый колебательный контур выделяет в конечном итоге несколько частоту, а целую полосу частот. Полоса частот, выделяемых колебательным контуром, именуется полосой пропускания колебательного контура. Ширина полосы пропускания измеряется в герцах, килогерцах, мегагерцах. Она зависит от качества колебательного контура: чем выше добротность, тем уже полоса пропускания. Ширину полосы пропускания возможно подсчитать по следующей несложной формуле. Ясно, что чем уже полоса пропускания, тем лучше избирательность контура, тем лучше он разделяет сигналы, имеющие родные частоты, тем меньше воздействуют на него всевозможные помехи.
Расстройка
Применение на практике последовательных колебательных контуров.
54. Параллельный колебательный контур
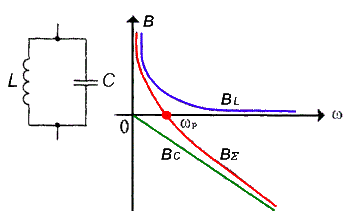
В разных радиотехнических устройствах наровне с последовательными колебательными контурами довольно часто (кроме того чаще, чем последовательные) используют параллельные колебательные контуры На рисунке приведена принципиальная схема параллельного колебательного контура. Тут параллельно включены два реактивных элемента с различным характером реактивности Как мы знаем, при параллельном включении элементов складывать их сопротивления запрещено — возможно только складывать проводимости. На рисунке приведены графические зависимости реактивных проводимостей катушки индуктивности BL = 1/?L, конденсатора ВC = -?C, и суммарной проводимости В?, этих двух элементов, являющаяся реактивной проводимостью параллельного колебательного контура. Подобно, как и для последовательного колебательного контура, имеется некая частота, именуемая резонансной, на которой реактивные сопротивления (соответственно и конденсатора) и проводимости катушки однообразны. На данной частоте суммарная проводимость параллельного колебательного контура без утрат обращается в нуль. Это значит, что на данной частоте колебательный контур владеет вечно громадным сопротивлением переменному току.
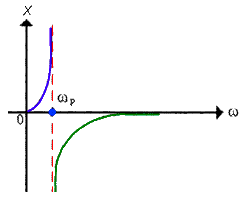
В случае, если выстроить зависимость реактивного сопротивления контура от частоты X? = 1/B?, эта кривая, изображённая на следующем рисунке, в точке ? = ?р будет иметь разрыв второго рода. Сопротивление настоящего параллельного колебательного контура (т.е с утратами), очевидно, не равняется бесконечности — оно тем меньше, чем больше омическое сопротивление утрат в контуре, т.е значительно уменьшается прямо пропорционально уменьшению добротности контура. В целом, физический суть понятий добротности, резонансной частоты и характеристического сопротивления колебательного контура, и их расчетные формулы, честны как для последовательного, так и для параллельного колебательного контура.
Для параллельного колебательного контура, в котором индуктивность, сопротивление и ёмкость включены параллельно, добротность вычисляется:
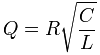 ,где R, L и C — сопротивление, ёмкость и индуктивность резонансной цепи, соответственно.
,где R, L и C — сопротивление, ёмкость и индуктивность резонансной цепи, соответственно.
Резонанс токов, условие его происхождения
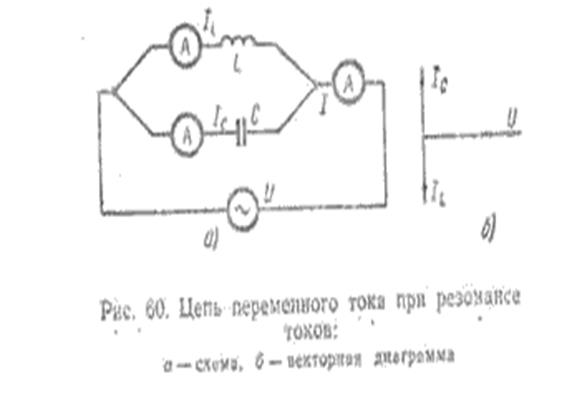
Резонанс токов. Резонанс токов может появиться при ёмкости и параллельном соединении индуктивности (рис 198 а). В совершенном случае, в то время, когда в параллельных ветвях отсутствует активное сопротивление (R1=R2 = 0), условием резонанса токов есть равенство реактивных сопротивлений ветвей, содержащих ёмкость и индуктивность. Так как в разглядываемом случае активная проводимость G = 0, ток в неразветвленной части
цепи при резонансе I=U(G2+(BL-BC)2)= 0. Значения токов в ветвях I1 и I2 будут равны(рис 198 б) , но токи будут перемещены по фазе на 180° (ток L в индуктивности отстает по фазе от напряжения U на 90°, а ток в емкости С опережает напряжение U на 90°). Следовательно, таковой резонансный контур представляет собой для тока I вечно электрическая энергия и большое сопротивление в контур от источника не поступает. Одновременно с этим в контура протекают токи IL и IС, т. е. имеет место процесс постоянного обмена энергией в контура. Эта энергия переходит из индуктивности в емкость и обратно.
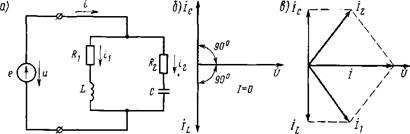
Показатели резонанса токов
При, в то время, когда частота колебаний генератора сходится с резонансной частотой контура его индуктивная и емкостная ветви оказывают равное сопротивление переменному току, в следствие чего токи в ветвях контура будут однообразными. В этом случае говорят, что в цепи имеет место резонанс токов. Как и при последовательного колебательного контура, конденсатора и реактивности катушки компенсируют друг друга, и сопротивление контура протекающему через него току делается чисто активным (резистивным). Величина этого сопротивления, довольно часто именуемого в технике эквивалентным, определяется произведением добротности контура на его характеристическое сопротивление Rэкв = Q·?. На частотах, хороших от резонансной, сопротивление контура значительно уменьшается и получает реактивный темперамент на более низких частотах — индуктивный (потому, что реактивное сопротивление индуктивности падает при уменьшении частоты), а на более высоких — напротив, емкостной (т к реактивное сопротивление емкости падает с ростом частоты)
Резонансная частота
Резонансной частотой контура именуют такую частоту, на которой сопротивление контура имеет чисто деятельный (резистивный) темперамент. Условие резонанса — это равенство размеров реактивных ёмкости катушки и сопротивлений индуктивности.
Векторная диаграмма
Выстроим векторную диаграмму для разглядываемой цепи (рис. 60, б) при резонансе токов. Отложим в выбранном нами масштабе вектор напряжения U. Ток в индуктивности отстает от напряжения на угол j = 90°. Исходя из этого вектор тока IL отложим вниз под углом 90° к вектору напряжения U. Так как ток в емкости опережает напряжение на угол j=90°, то вектор тока Iс, равный по условию резонанса токов вектору тока IL, отложим вверх под углом 90° вектору напряжения U.
На векторной диаграмме видно, что ток в индуктивности и том в емкости перемещены по фазе на угол j=180 (градусов) и равны друг другу. Из этого следует, что неспециализированный ток при резонансе токов равен нулю, а полное сопротивление цепи вечно громадно.
В конечном итоге неспециализированный ток будет довольно мелок, но не равен нулю. Данный ток, что производит генератор, есть активным и покрывает утраты энергии в контуре.
55.
- Параллельный колебательный контур. Полное эквивалентное сопротивление контура при резонансе и при расстройках, его активная и реактивная составляющие. Эквивалентная добротность параллельного контура с учётом влияния внутреннего сопротивления генератора.
В параллельном колебательном контуре катушка и конденсатор индуктивности соединены параллельно. В случае, если снабдить таковой контур энергией, к примеру, зарядив конденсатор, либо приведя к току в катушке индуктивности, то потом энергия будет перетекать из конденсатора в катушку и обратно. На конденсаторе будет формироваться синусоидальное напряжение. Его частота именуется частотой резонанса параллельного колебательного контура. Если бы не было утрат, то колебания длились бы вечно, но из-за утрат колебания понемногу затухают.
Контур, настроенный в резонанс , имеет большое активное сопротивление:
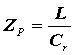
Расстройка контура ведет к изменению и уменьшению характера его реактивности. При , при
Избирательность контура в этом случае равна:
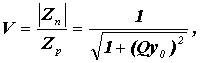
Контуры параллельного типа в зависимости от метода подключения к источнику переменного напряжения дробят на контуры первого, второго и третьего видов.
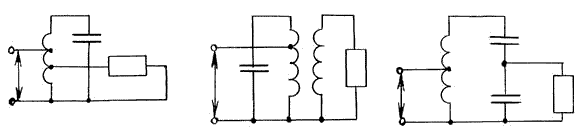
эквивалентное сопротивление контуров параллельного типа при резонансе токов равняется:
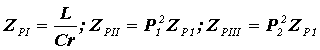 ,
,
Подключение нагрузки к контуру увеличивает сопротивление утрат контура, сокращает и , снижает его избирательность V
И увеличивает полосу пропускания
Для повышения избирательности используют колебательные совокупности, складывающиеся из двух либо более связанных между собой контуров.
Добро?тность — черта колебательной совокупности, определяющая полосу резонанса и показывающая, во какое количество раз запасы энергии в совокупности больше, чем утраты энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в совокупности. Другими словами, чем выше добротность колебательной совокупности, тем меньше утраты энергии за любой период и тем медленнее затухают колебания.
Неспециализированная формула для добротности любой колебательной совокупности:
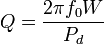 ,где:
,где:
- — резонансная частота колебаний
- — энергия, запасённая в колебательной совокупности
- — рассеиваемая мощность.
Параллельный колебательный контур. Амплитудно-частотные и фазо-частотные характеристики параллельного контура. Полоса пропускания контура и её зависимость от внутреннего сопротивления генератора. Избирательность параллельного контура при разных внутренних сопротивлениях генератора.
АЧХ
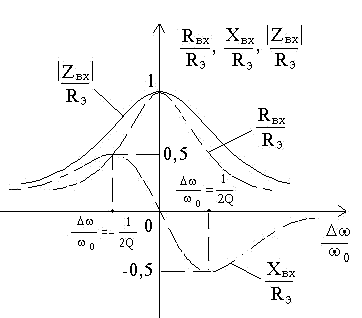
ФЧХ