Мыслитель. Скульптура О.РОДЕНА.
Выше говорилось, что мышление человека неотделимо от разрешения какой-либо неприятности, задачи, от поиска ответа на вопрос. И первый этап ответа задачи пребывает в правильном формулировании ее вопроса, в постановке самой задачи.
В случае, если человек говорит, что он о чем-то думает, а сам не имеет возможности сообщить конкретно, о чем, то сейчас настоящего мышления у него нет. Ему лишь думается, что он думает.
Время от времени перед отечественным умственным взглядом проносятся нерасчлененные образы, обрывки фраз — и мы можем быть полностью поглощены ими, принимая это как размышление. Особенно довольно часто так происходит при усталости либо болезни, при переутомлении. Но в случае, если нас спросят: какой вопрос разрешает отечественная идея, что мы желаем отыскать, — то мы не сможем сообщить ничего вразумительного, конкретного. И напротив, умение совершенно верно сформулировать вопрос, проблему — это уже начало настоящего мышления.
Во многих случаях эти вопросы ставит перед нами сама жизнь либо окружающие люди, но по большей части это зависит от нас и отечественной любознательности. Любопытный человек видит и ставит вопросы в том месте, где у других они не появляются. Умение подмечать в жизни нерешенные вопросы и пробовать решать их — первый показатель мыслящего человека.
Второй этап ответа задачи — рассмотрение условий, выяснение их точного содержания и состава, как время от времени говорят, данных, каковые необходимо учитывать при поиске ответа на вопрос. Это — тяжёлое дело, и оно не всегда сходу удается.
Для примера попытаемся решить такую несложную задачу:
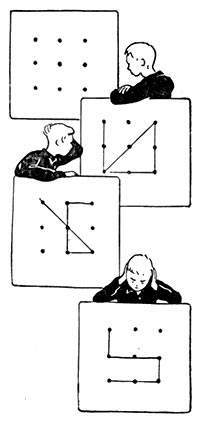«Даны 9 точек (см. рис.). Не отрывая карандаша от бумаги, необходимо перечеркнуть их четырьмя прямыми линиями».
Попытайтесь выполнить требования задачи. Вот вы сделали одну попытку, другую, третью (см. рис.).
Не получается?!
Из каких же условий вы исходите? «9 точек необходимо перечеркнуть четырьмя прямыми, не отрывая карандаша…» — думается, ваше ответ этому удовлетворяет.
Так отчего же все-таки у вас не получается?
Разглядите чертеж внимательнее, сопоставьте еще раз собственный воздействие с условиями.
Вы проводили линии лишь в квадрата, очерченного точками! Но для того чтобы условия в задаче нет. Вы создали его себе сами, подчиняясь изюминкам чертежа. Отбросим это невольное ограничение и будем проводить линии вне квадрата — тогда ответ возможно отыскать скоро (см. рис.).
Итак, не разглядев правильных условий задачи, решить ее верно запрещено. Самый распространенными неточностями наряду с этим бывают или приписывание условиям того, чего в них нет (как в задаче с точками), или, напротив, неучет того, что в них содержится. При ответе задач об этом направляться постоянно помнить.
Для проверки собственного умения устанавливать правильный состав условий попытайтесь решить следующие задачи:
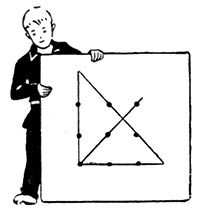
1. Из шести спичек выстройте 4 равносторонних треугольника со сторонами, равными длине одной спички.
2. Чему равен вес кирпича, если он весит 1 кГ и еще столько, сколько весит добрая половина кирпича? (Ответы даны в конце статьи.)
Узнав состав условий, мы переходим к третьему, ответственному этапу ответа задачи — к поискам самого ответа. Данный поиск содержит, в большинстве случаев, две стадии: сначала выдвигается предположение (догадка) о вероятном ответе, а после этого оно проверяется.
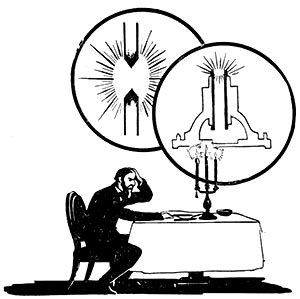
Разглядим, как решал одну техническую задачу известный русский ученый П. Н. Яблочков. Он продолжительное время занимался усовершенствованием электрической дуговой лампы. В лампах, использовавшихся до изобретения Яблочкова, угли размешались на одной прямой линии горящими финишами друг к другу. Понемногу угли сгорали, расстояние между ними возрастало, и лампа меркла (см. рис.). Существовало пара совокупностей регуляторов сближения углей по мере их сгорания, но все они были ненадежны.
Яблочкову довольно продолжительное время не получалось придумать ничего нового, дабы сохранить постоянным расстояние между углями. Но вот в один раз, как говорит его биограф, изобретатель сидел за столиком в кафе. Он весьма устал по окончании целого дня напряженной работы и сейчас, в ожидании обеда, рассеянно и машинально игрался карандашом. Случайно он положил его параллельно второму карандашу, лежавшему на бумагах, — и внезапно рассеянность его как ветром сдуло. А ну как расположить угли совершенно верно так, как эти карандаши — параллельно, — и совершить электродугу между ними? Тогда никакого сближения не потребуется и протяженность дуги будет постоянной (см. рис.).
Яблочков проверил это предположение и по окончании преодоления некоторых технических трудностей убедился в его правильности. Задача была решена.
На первый взгляд думается, что тут помог случай. В действительности это, само собой разумеется, не так. Изобретатель довольно много трудился над этим вопросом, всегда думал о нем, и лишь исходя из этого простые карандаши связались в его уме с электродами.
Бессчётные изучения процесса мышления при ответе задач (учебных, практических, научных) продемонстрировали, что предположение о ходе ответа часто появляется, в то время, когда человек разглядывает какой-либо второй материал. При попытках решить какую-либо задачу у человека создается «предчувствие» того, что должно быть ответом, но что именно — он еще не знает. Но сейчас кроме того маленькая подсказка со стороны сходу может натолкнуть его на решение. Человек как бы выясняет в ней то, что ему необходимо.
Иногда такими подсказками бывают весьма далекие от задачи предметы. Вот как было сделано одно открытие германским химиком прошлого столетия Кекуле. Он продолжительно думал, как изобразить молекулу бензола в виде таковой структурной формулы, которая отвечала бы особенностям бензола (его молекула содержит 6 атомов водорода и 6 атомов углерода— С6Н6).
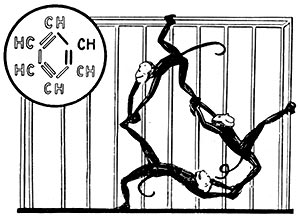Принцип построения таковой формулы был отыскан Кекуле очень нежданно и при необычных событиях. в один раз он заметил клетку с мартышками. Играясь, мартышки ловили друг друга. Один раз они схватились так, что составили кольцо. Любая мартышка одной ногой держалась за клетку, а обеими руками — за другую ногу соседней мартышки. В этом положении мартышки и образовали круг. Такое сложное распределение ног и рук животных натолкнуло ученого на идея: «Вот изображение формулы бензола». И вправду, его молекула возможно представлена в виде кольца с двойными связями атомов углерода (см. рис.). Так появилась в химии новая структурная формула.
Выдвигая предположение о вероятном ответе, мы довольно часто обращаемся к собственному прошлому опыту, к знаниям, купленным при ответе вторых задач. Это, само собой разумеется, во многом оказывает помощь нам: так как довольно часто задачи бывают сходны, подобны друг другу. Но это же иногда и мешает верно подойти к новой задаче, не разрешает заметить в ней необычное, не шаблонное содержание, требующее особенного приема. Решим такую задачу.
«На полке слева направо стоят две книги: в одной 450 страниц, в второй 470. В книгах завелся червь. Он прогрыз их от первой страницы первой книги до последней страницы второй. какое количество всего страниц прогрыз червь?»
Попытайтесь скоро решить эту задачу. Что тут следует сделать и какой окажется ответ? Разумеется, 920 страниц — так как необходимо сложить количество первой книги с количеством второй, не так ли?
Многие так и рассуждают, опираясь на собственный опыт: «В случае, если имеются две книги, а червь прогрыз их от первой страницы первой книги до последней страницы второй, то значит необходимо сложить их количества». На первый взгляд это словно бы бы верно, и вывод, значит, оправдан. Но это правильно лишь на первый взгляд! Снова, но пристально прочтите задачу и представьте себе положение книг. Лучше нарисуйте их либо кроме того заберите две книги и поставьте слева направо. Проделали это? Додумались, в чем тут дело? Правильно: червь прогрыз всего-навсего… лишь верхнюю крышку переплета первой и нижнюю крышку переплета второй книги! Так как книги находились слева направо, и верхняя крышка переплета первой книги соприкасалась с нижней крышкой переплета второй книги (см. рис.).
Неточность в ответе данной задачи обычна, она видится у большинства людей, пробующих решить задачу сходу, схватив условия только в общем виде, а в остальном надеясь на собственный прошедший опыт.
Сейчас попытаемся решить другую задачу. Тут вам пригодится знание элементарной школьной геометрии.
«Предположим, что около Почвы по экватору натянута нить. Ее протяженность равна окружности Почвы. Вторая нить натянута около апельсина (она равна его окружности). К каждой нити присоединили отрезки длиной в один метр. Ясно, что сейчас между поверхностями апельсина и Земли и нитями появилось пространство, собственного рода зазор. Какова же величина зазоров около апельсина и Земли? Сравнимы ли эти величины?»
Сейчас сообщите, каково ваше первое предположение об ответе? Вряд ли мы навяжем вам собственный мнение, в случае, если сформулируем его так: «Эти зазоры тяжело сопоставимы. Что означает один метр, прибавленный к окружности земного шара! В отношении же мелкого апельсина данный метр значит довольно много. Около Почвы зазора практически не будет, а около апельсина он будет громадной».
Таковой ответ исходит из наглядного представления о размерах апельсина и земного шара. Но в случае, если их окружности вправду очень сильно разны по величине, то в определении зазоров имеется принципиальная неточность. Дабы ответить на верно поставленный в задаче вопрос, необходимо именно отвлечься от апельсина и наглядного сопоставления Земли и совершить геометрические расчеты. А они приведут совсем к второму ответу.
Как мы знаем из геометрии, протяженность окружности равна 2?R, где ? — постоянная величина, приближенно равная 3,14, a R — радиус окружности. Ясно, что радиусы апельсина и Земли весьма разны. Обозначим условно радиус Почвы буквой R, а апельсина — r. Тогда окружность Почвы будет 2?R, а апельсина — 2?r. В то время, когда к длине каждой окружности прибавили по одному метру нити, они стали соответственно равны: 2?R + 1 и 2?r + 1.
При трансформации длины окружностей изменились и их радиусы, поэтому-то и появились зазоры — отличие между старыми радиусами и новыми. Вы понимаете, что радиус равен длине окружности, дроблённой на 2?r. Из этого следует, что новый радиус окружности для Почвы равен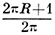 
, а для апельсина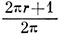 
Вычислим отличие между старым радиусами и новым.
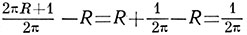
Отличие для Почвы:
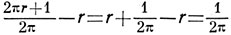
И вот вам ответ: отличие между старым радиусами и новым окружности для апельсина и Земли будет однообразной, то есть — 1/2? метра. В случае, если ? принять примерно за 3,0, то 2? будут равны 6, следовательно, и в том и другом случае зазор будет равен 1/6 м.
Так, строго математическое вычисление разрешило правильно, с учетом содержания данных условий, решить задачу, которая ошибочно решалась посредством привычных наглядных представлений.
Так, возможно сделать вывод, что при ответе задач нужно проводить правильное, строгое и, нужно, математически контролируемое рассуждение. На базе наглядных представлений многие задачи физики, других наук и химии решать весьма тяжело, а время от времени и просто нереально. Так как настоящие отношения вещей довольно часто не совпадают с тем, как они представляются на первый взгляд. Это необходимо постоянно помнить при столкновении с новыми, уникальными задачами и особенно строго контролировать начальные догадки о вероятном ходе ответа.
ОТВЕТЫ К ЗАДАЧАМ
1. Прочтя задачу, решающий в большинстве случаев начинает строить треугольники в одной плоскости — в плоскости стола, не смотря на то, что условие задачи этого не требует. Наряду с этим обнаруживается, что шести спичек для построения четырех треугольников слишком мало. Тогда решающий или отказывается от задачи, или пробует выложить треугольники из спичек, сломанных пополам (это, само собой разумеется, не соответствует условию задачи).
Ответ же весьма легко: необходимо из трех спичек выложить равносторонний треугольник в плоскости стола, а остальные три спички поставить над ним «шатром» (каждую спичку-под углом к плоскости стола). Окажется объемная фигура .
2. Вторую задачу в большинстве случаев решают так: к 1 кГ прибавляют 0,5 кГ (т. е. «половину» веса кирпича), что, само собой разумеется, не соответствует настоящему ответу. Так как в случае, если принять его за верное, то вес кирпича будет 1,5 кГ, а добрая половина — 0,75 кГ. Тогда в соответствии с условию кирпич обязан весить 1 кГ — 0,75 кГ, а это противоречит уже отысканному числу. При верном ответе задаются вопросом: а какая часть кирпича весит 1 кГ? Так как в случае, если кирпич весит 1 кГ и еще столько, сколько весит добрая половина, то, значит, 1 кГ имеется вес второй половины кирпича! Целый кирпич весит 2 кГ.