1. Ввести значения и заполнить ими массив.
2. Отыскать среднее значение в массиве.
Var
a: array[1..10] of integer;
s: integer;
i:byte;
begin
s:=0;
for i:=1 to 10 do
begin
wtite(‘введите —’);
readln(a[i]);
s:=s+a[i];
end;
end.
16.Правила разработки цикла
Известно по крайней мере два класса задач, каковые приводят к появлению цикла:
- обработка либо формирование массивов — при переносе формулировки задачи типа
//типа
либо
//типа инициализировать/ввести массив
с объекта на любой его компонент приобретаем повторяющиеся подзадачи. Эту последовательность подзадач уменьшаем, записывая формулировку подзадачи один раз (в обобщенной форме) и повторяя в цикле. При ответе этого класса задач циклы разрабатываются сверху вниз.Число повторений в большинстве случаев определяется числом элементов массива, исходя из этого употребляются циклы for (со счетчиком).
- итерационные методы – методы, основанные на применении рекуррентных формул. При ответе задач этого (второго) класса циклы разрабатываются снизу-вверх. Рекуррентные формулы в большинстве случаев употребляются по причине того, что для понижения сложности вычислений (замена умножения — сложением, а возведения в степень — умножением и т.п.) на каждом шаге при каждом новом повторении цикла любой новый итог получается с применением ветхого (ранее взятого) результата. Возможно выделить 2 разновидности итерационных методов:
1. Методы, которые связаны с реализацией т.н. n-арных операций:
S =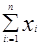 
=x1+x2+x3+…+xn S = 
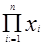= x1•x2•x3•…•xn S = X!=1•2•3•4•…•X и т.п.
Реализация n-арных операций требует преобразования их в последовательность двухместных (двоичных) операций, что ведет к появлению повторяющихся необходимости и действий сворачивания этих повторяющихся действий в цикл.
2. Методы приближенных вычислений — методы, разрабатываемые для постепенного (пошагового) приближенного нахождения ответа задач (к примеру, поиск корня уравнения), для которых неизвестно, как отыскать правильное ответ.
Обе задачи второго класса приводят к появлению циклов, каковые разрабатываются способом снизу вверх. Наряду с этим первая разновидность задач второго класса реализуется посредством циклов с известным числом повторений (цикла for — для каждой n-арной операции, зная n, возможно выяснить число повторений), а вторая разновидность — посредством циклов с малоизвестным числом повторений.
Как мы знаем, что структура цикла (с известным числом повторений) включает в себя три компонента: подготовка цикла, заголовок цикла, тело цикла (те действия, каковые нужно многократно повторить). Заголовок цикла задает правила трансформации параметра цикла (тело цикла повторяется для каждого значения параметра цикла).
В большинстве случаев, очередное повторение тела цикла строится с применением результата, взятого при прошлом повторении тела цикла, наприемр, как в этом случае
xi = xi-1 + h
yi = f(xi).
Наряду с этим подготовка цикла фактически имитирует такое исполнение тела цикла, которого еще не было. Это делается после этого, дабы настроить тело цикла на первое верное исполнение.
Но, в случае, если цикл организован так, что очередное повторение тела цикла не применяет итог прошлого повторения, как в этом случае
xi = (i-1)*h и yi = f(xi)
то в этом случае подготовка цикла не нужна.
Порядок разработки циклов восходящим способом:
1. Записываем линейный метод (в котором, к примеру, многоместная операция реализуется посредством последовательности громадного количества двоичных операций).
2. Находим рекуррентную формулу (подмечаем повторяемость) для определенной последовательности шагов.
3. Те повторяющиеся действия, для которых удалось взять обобщенную формулу, сворачиваем в цикл. Наряду с этим в тело цикла попадают те действия, каковые записаны в виде рекуррентной формулу; в заголовке цикла записываем правило, благодаря которому устанавливается, повторять потом цикл либо нет; в подготовку цикла включаются те действия, каковые не удалось обобщить.
4. В случае, если подготовка цикла не несложная, то нужно выполнить ее упрощение.
5. В случае, если попытка упрощения подготовки цикла удалась, то нужно скорректировать заголовок так, дабы число повторений стало на 1 больше.
6. Нужно выполнить операцию отбрасывания лишних индексов.
Сейчас о том, в то время, когда циклы разрабатываются способом сверху вниз. Возвратимся к уточнению команд обработки цикла.
При появлении команд:
Организовать массив
либо
Обработать массив
Пример:
ввести массив
либо
вывести массив не связано с накоплением и вычислением значений
либо
присвоить массив массиву
Но не:
Отыскать сумму элементов массива связано с накоплением
Отыскать минимальный либо большой элемент массива значений
эти команды (из верхних примеров) уточняются следующим образом: потому, что объект (массив) владеет однородной внутренней структурой, мы можем воспользоваться стандартным правилом уточнения команд и перенести исходную задачу на любой элемент массива (компонент объекта).
В следствии получается много формулировок команд следующего вида:
обработать первую компоненту
обработка массива обработать вторую компоненту
………………………………………………..
обработать n-ую компоненту
уточнение
Как мы знаем, наличие громадного количества повторяющихся формулировок команд приводит к необходимости сворачивания их в цикл, в отличие от разработки цикла восходящим способом. В этом случае появление циклов возможно предвидеть, наряду с этим нет необходимости сначала записывать линейный метод, обнаружить обобщенную запись и т. д. В этом случае цикл разрабатывается способом сверху вниз, и такая разработка включает в себя следующие шаги:
1. Сходу возможно записать тело цикла, имеющее одну из следующих 2 форм:
| организовать i-ю компоненту либо обработать i-ю компоненту |
2. Возможно сходу записать заголовок цикла, в котором в качестве параметра цикла возможно применять индекс (номер) элементов массива. Закон трансформации параметра цикла, либо количество повторений цикла, будет определяться числом компонент, каковые нужно обработать.
К примеру:
For i := to do …
где i – параметр цикла.
3. В соответствии с ранее сформулированному правилу с учетом того, что тело цикла в большинстве случаев не применяет итог прошлого, подготовка цикла в большинстве случаев не нужна. Выше было продемонстрировано, что подготовка цикла нужна лишь при формулировок задач вида
— Отыскать сумму элементов массива
— Отыскать минимальный либо большой элемент массива
и т.п.
Действия над массивами
15.6.1 Возможно присваивать содержимое одного массива второму, но не всегда.
Type
t = array [1..10] of byte;
Var
a, b: array [1..10] of byte;
c: array [1..10] of byte
e, f: t;
| Верно |
begin
a := направляться;
e := f;
| Неправильно |
a := c;
e := a;
Правило, по которому неправильное отделяется от верного, весьма простое: вы имеете возможность присвоить содержимое лишь таких массивов, у которых эквивалентны типы в соответствии с объявлению.
Тип С неэквивалентен типам А и В. Если бы необходимо было сделать тип С эквивалентным типам А и В, то необходимо:
a, b, c: array [1..10] of byte;
Замечание: не смотря на то, что возможно присваивать содержимое одного массива второму, вы запрещено их сравнивать.
if a = b then … — запрещено.
Исходя из этого, в случае, если необходимо сравнить 2 массива, то их сравнивать придется посимвольно (не считая символьных массивов, каковые в Паскале эквивалентны строчкам).
15.6.2 Инициализация массивов.
Замечание: в отличие от языка Си, где имеется старт языка т в соответствии с этому стандарту все глобальные переменные, а также массивы, в начале исполнения программы инициализируются нулями, для Паскаля (Турбо-Паскаля) нет стандарта (данный язык — внутренняя разработка компании Борланд) и массивы (в зависимости от реализации) смогут не инициализироваться (инициализироваться всяким мусором — не обязаны инициализироваться непременно 0). Исходя из этого для определенности нужно перед применением массивов задать им начальное значение. Для этого имеется три пути:
1. Применение типизированных констант (уже разглядели выше)
2. 
Применение цикла (по элементам)
3. 
Применение специальной функции Fillchar().
Применение цикла (по элементам)
Var
a: array [1..5] of byte;
i: byte;
begin
randomize;
for i := 1 to 5 do
a[i] := i; // элементы массива инициализируются значениями параметра цикла
либо
a[i] := random(100); // элементы массива инициализируются псевдослучайными числами
либо
| begin write(‘a[‘, i, ‘] = ‘); readln(a[i]) end; |
// элементы массива инициализируются в диалоге с пользователем
 |
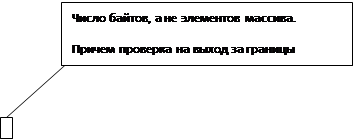Применение процедуры Fillchar(): типа char
Fillchar(имя массива, число байт (не элементов), значение) — заполняет побайтно всю область памяти под массив заданным значением {fillchar (a, 5 ,#0);}, причём проверка на выход за границы массива не выполняется.
Пользоваться данной процедурой нужно бережно: в случае, если тип элемента массива будет не byte, а integer, то fillchar (a,5,#1) забьет массив значением 257, а не 1. Помимо этого, если бы тип элементов был integer, нужно было бы писать 5*sizeof(integer) вместо 5.
15.6.3 Элементы массива возможно применять везде, где возможно применять простые скалярные переменные (в процедурах ввода и операторах присваивания-вывода и т.п.)
15.6.4 Обмен значениями между подмассивами и между массивом и подмассивами
15.6.4.1 Обмен между подмассивами
Подмассив – часть массива, к которой возможно обратиться, применяя число индексов, меньшее чем число размерностей массива. Более неспециализированное наименование подмассива – сечение. В языке PL/I: А(1,*) – 1-я строчок, А(*,1) – 1-я колонка массива. В Паскале сечения вероятны лишь для строчков: A[1] – первая строчок n-мерного массива.
Правило (выше было дано): тип элемента массива определяется тем, сколько индексов указано по окончании имени массива.
Разглядим пример:
Const N=3;
Var
A: array[1..2, 1..N] of byte;
B: array[1..2, 1..N] of byte;
Begin возможно применять sizeof(тип элемента)*число_ячеек
Fillchar(a, sizeof(a) div 2, 1); ————- заполнение 1-ой строки единицами (верно)
Fillchar(a[2,1], sizeof(a) div 2, 2); ————- заполнение 2-ой строки двойками (неправильно)
возможно и без того: round(sizeof(a)/2) — в отличие от DIV деление посредством ‘/’ постоянно даёт вещественный итог
Замечание. Так показывать параметр fillchar запрещено (и указатель применять также запрещено)
Нужно (возможно) один из двух вариантов:
1) Fillchar(a, sizeof(a), 2); //целый массив а заполняем двойками
Fillchar(а, sizeof(a) div 2, 0); //первую строчок очищаем от двоек
2) Fillchar(a[2], sizeof(a) div 2, 2); //вторую строкузаполняем двойками
a[1] := a[2]; ——— возможно ——- обмен между 1 и 2 строчками одного массива
b[1] := a[2]; ——— запрещено (типы не эквивалентны)
Правило: Обмениваться смогут подмассивы лишь эквивалентных типов.
Но это правило возможно обойти следующим образом. Пускай нужно b[1] := a[2].
Move( a[2], — 1 довод (откуда брать)
b[1], — 2 довод (куда помещать)
sizeof(a) div 2); — 3 довод (какое количество переслать байтов)
Эта процедура байты из одного места в памяти в второе (диагностику типа этих байтов она не делает).
15.6.4.2 Обмен между подмассивом и массивом
Разглядим сходу Пример:
Type
t=array[1..3] of byte;
Var
A: array[1..2, 1..3] of byte;
B: t;
C: array[1..2] of t;
Begin тип A[2] = array[1..3] of byte (? t)
A[2] := b; ————————- запрещено (типы не эквивалентны)
тип b = t
C[2] := b; ————————- возможно (тип c[2] = t = тип b)
Move(b, a[2], sizeof(b)); ——- возможно
B := a[2]; ————————— запрещено
B := t(a[2]); ————————— возможно
Move(a[2], b, sizeof(b)); ——- возможно
B := c[2]; ——————— возможно
15.6.5 Сдвиг значений в массива
15.6.5.1 Сдвиг элементов одномерного массива вправо
Задача: нужно выполнить сдвиг заданной части массива M (начиная с позиции i1 (пускай i1=3) и заканчивая позицией i2 (пускай i2=7) на заданное число позиций вправо (пускай = 2).
Изображение постановки задачи имеет форму:
Var M: array[1..11] of byte; Используем разработку цикла восходящим
| m[9]:=m[7] m[8]:=m[6] m[7]:=m[5] m[6]:=m[4] m[5]:=m[3] i j | Обобщенная запись: M[i] := M[j] = M[a*i+b] |
i1 i2 i значительно уменьшается способом и возьмём следующий линейный
метод:
| Mj |
| Mi |
Массив одномерный и для прохода по нему достаточно одного индекса – i (а у нас в обобщенной записи – два индекса). Дабы избавиться от второго индекса (j), нужно в общем случае выразить зависимость j от i. В общем виде эта зависимость линейная (возможно по точкам выстроить зависимость j от i для проверки) и имеет форму: j := a*i + b
Для нахождения a и b нужно составить совокупность уравнений (из линейного метода):
7 = a*9 + b
6 = a*8 + b
j i
Сейчас возможно записать цикл. НО:
Запрещено
(глядя на рисунок выше написать)
i1 + i3 i2 + i3-1
For i:= 5 to 9 do
M[i] := M[i-2];
Тут новые значения преждевременно
будут затирать ветхие
Нужно число байт
| For i:=9 downto 5 do m[i] := m[i-2]; т.е. двигаться по массиву при сдвиге вправо нужно в направлении, противоположном направлению сдвига, т.е. влево. | Move[a[5], a[3], 5); // сдвиг влево Move[a[3], a[5], 5); // сдвиг вправо для произвольного типа нужно писать так: (i2 – i1 + 1) * (sizeof(тип элемента)) число пересылаемых число байт на один элемент элементов | |
| Процедура Move в любой момент верно выполняется (она сама в верном порядке расставляет операторы присваивания) |
Самостоятельно: разобрать сдвиг массива влево.
15.6.6 Поиск элемента (одномерного ) массива
Поиск – это нахождение индекса(ов) элемента(ов), значение которого удовлетворяет некоему установленному правилу (критерию). В большинстве случаев в качестве критерия принимают равенство эталону.
Поиск
 |
 |
|||||
| label уходим; Const L=1; H=10; Var A: array[L..не of integer; эталон: integer; Итог: Longint; Нашли: Boolean; Середина, Низ, Верх: Longint; //текущие границы промежутка Begin Низ := L; {левая граница промежутка} Верх := H; {правая граница промежутка } Нашли := FALSE; {показатель того, что нашли} Середина:= 0; {индекс середины промежутка между Верх и Низ} Итог := 0; {индекс искомого элемента} эталон := ….; {то, что ищем} {Проверка — имеется ли искомый эталон в массиве?} IF (A[Низ] эталон) OR (A[Верх] эталон) then begin writeln(‘Совпадение искать безтолку’); goto уходим; end; Repeat Середина := round((Верх+Низ)/2); IF A[Середина] эталон then Верх := Середина //эталон в левой половине else if A[Середина] эталон then Низ := Середина //эталон в правой половине else Нашли := TRUE; // значит A[Середина] = эталон until (Нашли=TRUE) OR (Низ = Верх)) IF Нашли = TRUE then Итог := Середина {в Итог — индекс искомого элемента} else writeln(«Совпадений не отыскано.») уходим:; end. |
В начале бинарного поиска имеем 2 обстановке:
| Обстановка | Воздействие |
 Эталон в массиве имеется |
Отыскать |
| Эталона в массиве нет (A[Низ] эталон) OR (A[Верх] эталон) | Сообщение |
цикл, где на каждом повторе вычисляем новую
середину и разбираем 3 обстановке:
| Обстановка | Воздействие |
| Эталон в левой половине (A[Середина] эталон) | Верх := Середина |
| Эталон в правой половине (A[Середина] эталон) | Низ := Середина |
 Эталон ровно в середине (A[Середина] = эталон) |
Нашли := True Итог := Середина |
выход из цикла := ((Нашли = True) OR
(Низ = Верх))
Мы разглядели обстановку, в то время, когда поиск выполняется лишь по одному критерию (показателю). Поиск по нескольким параметрам возможно выполнен:
см. Однопроходные методы (индуктивные функции) в Кушниренко, Лебедев «Программирование для математиков»
а) За один проход по массиву (файлу, перечню, последовательности) — возможно выполнен, в случае, если удовлетворение запроса не связано с накоплением статистики и ее последующим анализом (накопленной статистики).
К примеру: выбрать из всех студентов лишь мужского пола ростом выше 1.8м и не старше 20 лет.
Тут возможно записать обобщенный критерий поиска в виде логического выражения
П1 и П2 и П3
Пол = мужской рост = 180 см возраст
Задача поиска сводится к однократному проходу по отбору и массиву на протяжении прохода тех студентов, характеристики которых обращают приведенное логическое выражение в истину (TRUE):
Repeat
if (П1 and П2 and П3)
then отобрать
else искать дальше
перейти к следующему
until закончить
б) За пара проходов по массиву– в случае, если удовлетворение запроса связано с анализом и накоплением статистики.
К примеру: нужно выбрать из всех студентов лишь 3 студентов моложе 20 лет и ростом не ниже 180см каковые значительно чаще звонят (пишут) мне по окончании 22:00.
Слово чащев условии показывает, что нужно накопить статистику перед выбором.
Тут уже нужно разглядывать несколько критерий, а два (второй разрешит выбрать из тех, кого отобрали по первому критерию):
— критерий, по которому отбирается (накапливается) статистика;
— критерий отбора из того, что накопили.
Критерий для накопления статистики (какое количество раз звонил) обязан включать показатели:
— информация о поле студента;
— информация о возрасте студента;
— информация о росте студента;
— информация о времени звонка студента
и будет иметь вид, подобный рассмотренному выше
П1 и П2 и П3 и П4
Пол = мужской рост = 180 см возраст = 22
Решить поставленную задачу возможно по крайней мере так:
Сначала за первый проход выбираем (запоминаем число звонков) для всех тех студентов, каковые подходят по критерию, сформулированному выше. После этого за второй проход среди отобранных кандидатов контролируем (либо вычисляем, в случае, если при первом проходе было лень вычислять) число звонков и выбираем тех, у кого это число больше.
15.6.7 Сортировка элементов (одномерного) массива (для ускорения поиска в массиве)
Сортировка — размещение (переупорядочивание) элементов по определенному критерию. В большинстве случаев — по убыванию (descend) либо возрастанию (ascend). Существует довольно много способов сортировки. Несложный, но не самый нехороший (лучший) — сортировка выбором. Разглядим, как выполнить сортировку по убыванию. Для этого нужно:
— сперва последовательно разглядывать кандидатов на место самого первого элемента (самого громадного), по окончании чего громаднейший из кандидатов делается первым (обменивается с первым);
— после этого среди оставшихся (N-1) элементов массива последовательно рассматриваются кандидаты на место 2-го элемента и громаднейший из кандидатов при просмотре делается вторым (обменивается со вторым элементом);
— и т.д.
Разумеется, что число просматриваемых элементов с каждым шагом значительно уменьшается.
Введем обозначения:
i – индекс элемента, на место которого ищем кандидата
j – индекс элемента, что мы просматриваем в качестве кандидата
i=1 i=2 i=3 i=4 i=5
1 3 4 2 5— Исходное состояние массива
3 1 4 2 5—-После итерации для j=2———-i = 1 j = 2
4 1 3 2 5—-После итерации для j=3———-i = 1 j = 3 i = 1
4 1 3 2 5—-После итерации для j=4———-i = 1 j = 4
5 1 3 2 4—-После итерации для j=5———-i = 1 j = 5
——————————————————————
5 3 1 2 4—-После итерации для j=3———-i = 2 j = 3
5 3 1 2 4—-После итерации для j=4———-i = 2 j = 4 i = 2
5 4 1 2 3—-После итерации для j=5———-i = 2 j = 5
——————————————————————
5 4 2 1 3—-После итерации для j=4———-i = 3 j = 4 i = 3
5 4 3 1 2—-После итерации для j=5———-i = 3 j = 5
——————————————————————
5 4 3 2 1—- По окончании итерации для j=5———i = 4 j = 5 i = 4
Возможно подметить:
— при поиске каждого нового кандидата число просматриваемых элементов значительно уменьшается на единицу;
— при поиске кандидата на I-ое место I фиксируется, а J пробегает значения от I+1 до N.
Разумеется, что требуется два цикла:
— внешний по элементам, для которых ищем кандидата (цикл по параметру I, где I изменяется от 1 до N-1);
— внутренний по элементам-кандидатам (цикл по параметру J, где J изменяется от I+1 до N).
В итоге возьмём следующий фрагмент программы:
for i:= 1 to N-1 do
for j:=i+1 to N do
ему ищем замену
| … |
| a[i] |
| … |
| a[j] |
| … |
if ( a[j] a[i] ) // в случае, если кандидат больше по значению, чем текущий
кандидат
then
| R |
begin
1) R := a[i]; //дабы не утратить значение переменной a[i]
2) a[i] = a[j];
3) a[j] = R;
end;
Замечания: по поводу реализации массивов в Паскале:
1. Число размерностей массива ничем не ограничено, но размер массива как любой статической переменной в памяти ограничен 64 Кб (нельзя объявить тип размером 64 Кб).
2. Индексы смогут быть как хорошими, так и отрицательными.
3. Тип индексов возможно любым порядковым, не считая типа longint.
4. В Турбо-Паскале имеется два режима компиляции, имеющие отношение к массивам:
{$R+} и {$R-} — выполняется либо нет проверка, не выходит ли индекс за заявленные границы диапазона:
— в случае, если проверка выполняется, то при нарушении границ диапазона программа неудачно завершается с кодом 201 (Range Check Error);
— в случае, если проверка не выполняется, то при нарушении границ диапазона программа неудачно не завершается и никаких сообщений не выдается (но наряду с этим программа сама себя портит).
Примечание:
В случае, если отключить контроль диапазонов, возможно создать массив с переменными границами (вольный массив):
{$R-}
Var a: array [1..1] of integer:
Такое объявление показывает компилятору, что мы желаем иметь переменную а с индексом.
В случае, если по адресу а динамически выделить память, то возьмём массив для того чтобы размера, какого именно захотим (мы возвратимся к этому, в то время, когда будем разглядывать тему «Указатели»).
5. При передаче массивов как параметров в подпрограммы не рекомендуется определять тип массива конкретно в заголовке подпрограммы (из-за неосуществимости наряду с этим обеспечить эквивалентность типов фактического и формального параметров — массивов).
Замечание. Записать-то так при объявлении подпрограммы возможно (сама запись не есть неточность), но делать так не нужно из-за неприятностей с совместимостью дальше по тексту программы..
6. В качестве формального параметра подпрограммы возможно применять массив без границ (открытый массив).
Var
a: array of char;
Для работы с ними употребляются функции High (возвращает верхнюю границу индекса — в большинстве случаев = число элементов массива минус 1; не путать с Hi(x) для целый доводов) и Low (возвращает нижнюю границу индекса, в большинстве случаев = 0; не путать с Lo(x) для целых доводов).
Множества.