напряжение и Электрический ток изменяющиеся во времени по какому-либо закону именуют переменными.
В случае, если форма кривой напряжения и переменного тока повторяется через равные промежутки времени, то их именуют периодическими.
Мельчайшее время, через которое повторяется форма напряжения и переменного тока, именуют периодом, обозначают Т и измеряют в с.
Число периодов Тв 1 секунду именуют частотой f напряжения и переменного тока и дана размерность герц (Гц).
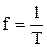, Гц
Несложными периодическими переменными напряжением и током являются вырабатываемые генераторами всех тока электростанций и видов напряжения (энергия) синусоидальной формы.
, А
, B
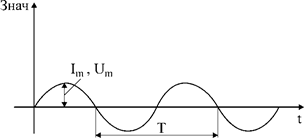
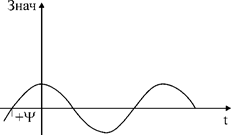
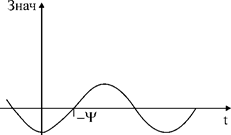
Тут обозначают:
i(t), u(t) – напряжения и мгновенное значение тока;
Im, Um – напряжения и амплитудные значения тока;
Yi, Yu – напряжения и начальная фаза тока, герц;
= 2p?f – угловая частота, с-1.
Отличие начальных фаз напряжения и тока обозначили j=Yu–Yi и назвали угол сдвига фаз.
Периодические напряжение и ток характеризуют еще понятиями действующего значения и среднего.
Среднее значение – это среднее значение за период. Так как у синусоидальной функции оно равняется нулю (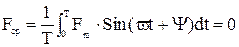 
), у напряжения и синусоидального тока за среднее значение определяют значение за полпериода ( ).
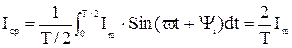, А
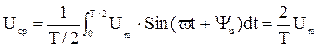, В
либо Iср=0,64 Im, Uср=0,64 Um.
Действующее значение периодической синусоидальной функции – это среднеквадратичное значение за период.
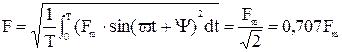
Тогда
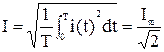, A
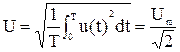, B
Нужно запомнить – отличие между амплитудным и действующим значением периодического напряжения и синусоидального тока – .
Измерительные устройства (амперметры. вольтметры) магнитоэлектрической совокупности показывают среднее (Iср, Uср) значение напряжения и синусоидального тока i(t), u(t).
Измерительные устройства (амперметры. вольтметры) электромагнитной, электродинамической, тепловой совокупностей показывают действующее значение (I, U) напряжения и синусоидального тока i(t), u(t).
По действующему значению I периодического синусоидального тока делают выводы о его тепловом действии: действующее значение I равняется постоянному току I0, что выделяет в активном сопротивлении R за один период Т столько же тепла, что и .
(I2R=I02R).
Мощность в электрических цепях периодического
Синусоидального тока.
Мгновенное значение мощности.
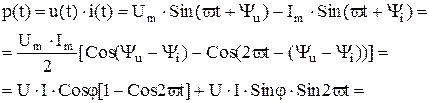
, BA
Тут обозначили и назвали:
U?I=S – полная мощность, ВА;
U?I?Cos j=P – активная мощность, Вт;
U?I?Sin j=Q – реактивная мощность, ВАР.
Разглядим поведение периодических синусоидальных токов и напряжений в отдельных элементах электрических цепей.
Активное сопротивление R.
 |
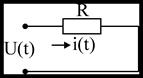т.е. в активном сопротивлении угол сдвига фаз j равен нулю, значит ток и напряжение в активном сопротивлении сходится по фазе (jR=Yu–Yi=0).
Среднее значение за период – активная мощность
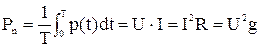
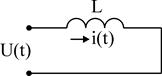Индуктивность L
, 
, 
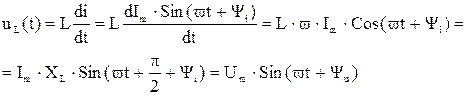
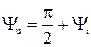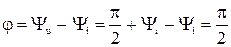
а величину XL= ?L именуют индуктивным сопротивлением и дали размерность Ом, величина обратная XL – индуктивная проводимость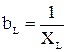 
.
Тут взяли два серьёзных момента:
— индуктивное сопротивление XL= ?L=2p?f?L, Ом;
— на совершенной индуктивности L угол сдвига фаз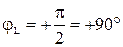 
, т.е. напряжение UL(t) опережает ток в индуктивности на 90°.
.
Видно, что активная мощность pL=0, a QL= U?I = I2?XL
Емкость C
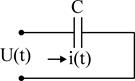
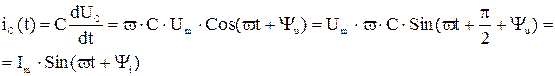
, bc – емкостная проводимость;
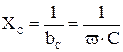– емкостное сопротивление, размерность – Ом.
.
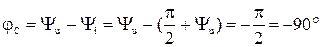Взяли две серьёзных момента:
— проводимость и ёмкостное сопротивление
, 
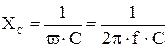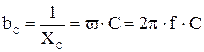
— на совершенной емкости С угол сдвига фаз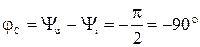 
, т.е. напряжение отстает от тока на угол 90°.
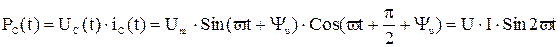
Как и на индуктивности, на емкости активная мощность PС=0, а реактивная QС= U?I = I2?XС
В случае, если напряжения и токи на R, L и С изобразить в виде векторов, то возможно видеть:
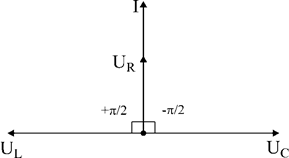
jR = 0
jL = +90°
jС = –90°
Отечественная задача – вычислить электрическую цепь, т.е. выяснить токи в ветвях и напряжения между узлами и на элементах, при действии периодических синусоидальных токов и напряжений.
Разглядим несложную цепь – последовательное соединение элементов R, L, C.
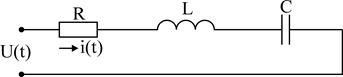
Допустим, что , т.е. . Тогда по второму закону Кирхгофа:
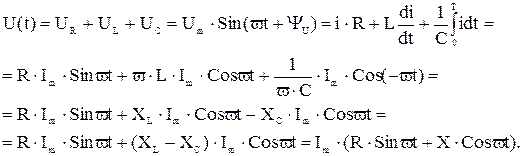
где величину XL–XC=X назвали реактивным сопротивлением.
(Видно, что X имеет символ ± , в зависимости что больше XL либо XC).
Применяя тригонометрию, возможно видеть:
;
,
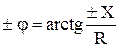где , назвали – полное сопротивление
В случае, если изобразить расчет напряжения в цепи в виде векторов, то возьмём:
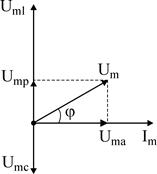
– цепь имеет индуктивный темперамент.
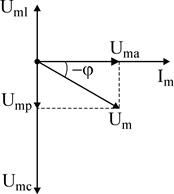
– цепь имеет емкостной темперамент.
Поделив все напряжения на ток, возможно взять треугольник сопротивлений.
; .
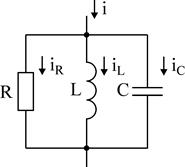Разглядим еще одну несложную цепь – из параллельного соединения R, L, C.
Допустим
,
.
По 1-му закону Кирхгофа:
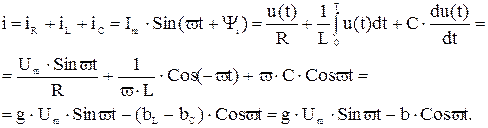
где
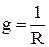– активная проводимость;
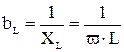– индуктивная проводимость;
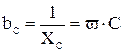– емкостная проводимость;
– реактивная проводимость.
( b, как и Х имеет символ ± в зависимости, что больше bL либо bC).
В случае, если изобразить расчет тока в цепи в виде векторов, то возьми:
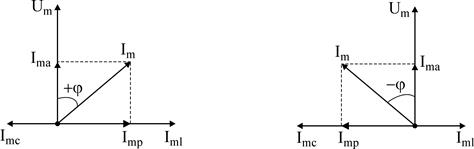
Поделив токи на напряжения, возьмём треугольник проводимостей.
;
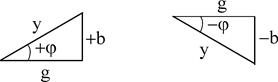
Этот метод расчетов электрических цепей при периодических напряжениях и синусоидальных токах, в то время, когда приходится все время оперировать синусоидальными (косинусоидальными) понятиями и функциями полных проводимостей и сопротивлений и применять при расчете векторные диаграммы по 1 и 2 законам Кирхгофа стал называться графо-аналитического способа.
Громадного применения, в особенности при сложных цепях, данный способ не взял, ввиду громадной сложности, в особенности при ручном расчете.
РЕАКТИВНЫЕ ДВУХПОЛЮСНИКИ.
самая простой электрической цепью есть двухполюсник – любой сложности схема, имеющая два зажима (входной, выходной).
Двухполюсники смогут быть разными:
— линейные, нелинейные;
— активные, пассивные;
— реактивные, с утратами и т.п. (зависит от черт элементов в схеме).
Мы разгляди линейные, пассивные, чисто реактивные (имеются катушки Li и емкости Ci) двухполюсники.
В виду того, что соотношения между мгновенными токами i(f) и напряжениями U(f) описываются интегрально-дифференциальными выражениями по 1 и 2 законам Кирхгофа, воспользуемся их изображениями по преобразованию Лапласа либо их аналогами для частных случаев.
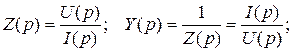
комплексная частота;
операторное индуктивное сопротивление;
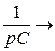операторное емкостное сопротивление;
операторное проводимость и реактивное сопротивление.
При гармоническом (синусоидальном, периодическом) действии .
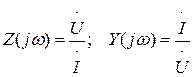
Зависимости от частоты.
Z(w), Y(w) – амплитудочастотная черта;
j(w) – фазочастотная черта.
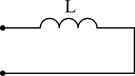Разглядим пара несложных схем реактивных двухполюсников:
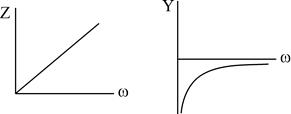
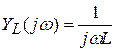
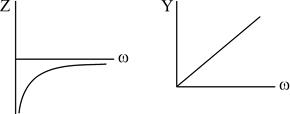
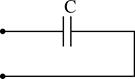
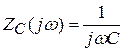
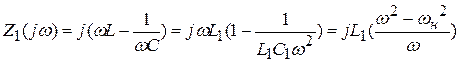
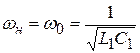
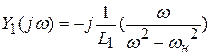
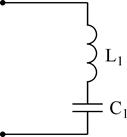
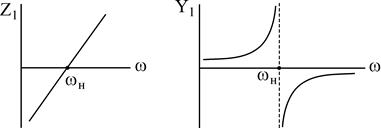
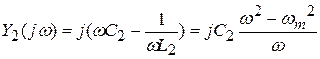
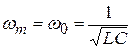
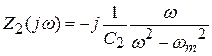
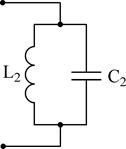
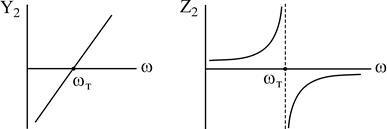
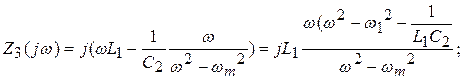
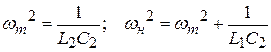
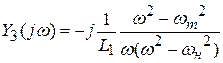
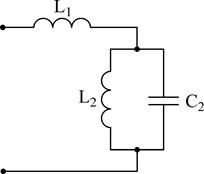
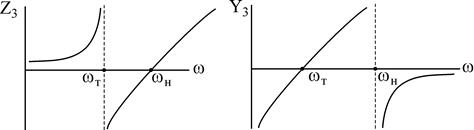
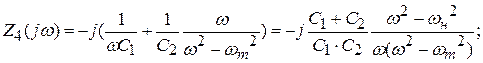
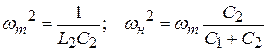
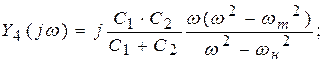
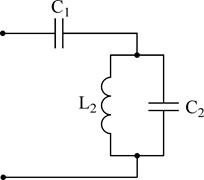
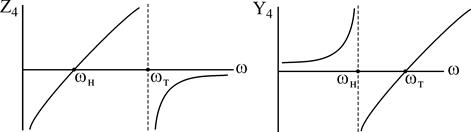
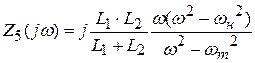
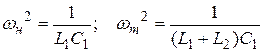
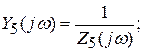
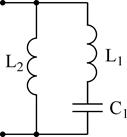
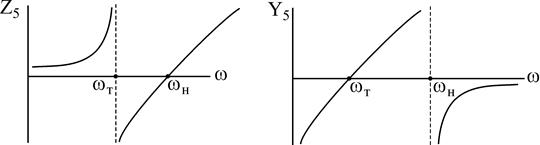
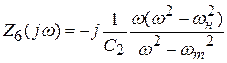
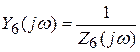
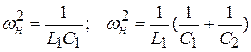
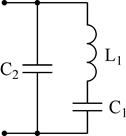
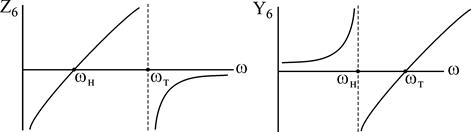
Сделав анализ рассмотренных схем, возможно видеть:
— число резонансов на единицу меньше числа элементов;
— АЧХ определяется чередованием нулей (резонанс токов) и полюсов (резонанс токов); в случае, если в схеме имеется путь для постоянного тока, то первым конкретным резонансом будет резонанс токов;
— крутизна АЧХ Z(ш), Y(ш) в любой момент хороша либо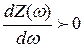 
(теорема Фостера);
— — в любой момент отношение двух полиномов ?, степени которых отличаются на 1;
— у некоторых схем АЧХ выглядят одинаково (Z3 и Z5), (Z4 и Z6), у некоторых обратно (Z3 и Z6, Z5 и Z6).
Два двухполюсника именуются обратными, в случае, если произведение их сопротивлений величина вещественная и хорошая, а амплитудо-частотные характеристики выглядят взаимообратно (изменяются местами полюса и нули).
В схемах обратных двухполюсников элементы дуальны (L-C) и изменяется вид соединений (последовательное — параллельное).
Два двухполюсника именуются эквивалентными, в случае, если при выражениях и разных схемах они имеют однообразного вида АЧХ. В схемах эквивалентных двухполюсников элементы имеют различные размеры, но изменяется вид соединений (последовательное-параллельное).
Канонические схемы двухполюсников.
Канонической именуют схему, которая при верном задании позволяет выполнить это задание.
В случае, если обобщить выражения входных сопротивлений несложных схем , то в общем случае выражение входного сопротивления двухполюсника будет иметь вид (в операторной форме):
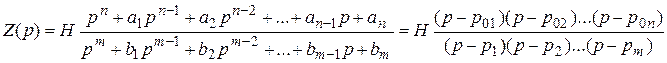
При :
Так как степени n и m либо равны либо отличаются не более чем на 1, а в любой момент нечетная функция ?, возможно лишь четыре вида , каковые назвали классами.
H, a, b – вещественные размеры, зависящие от параметров элементов схемы.
I класс.
знаменателя и Степени числителя однообразны (n=m).
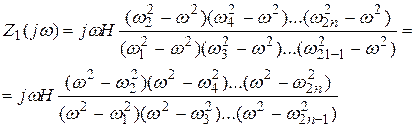
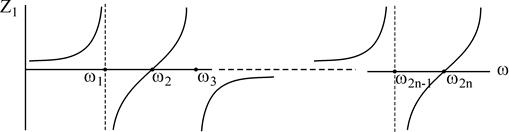
II класс.
знаменателя и Степени числителя однообразны (n=m).
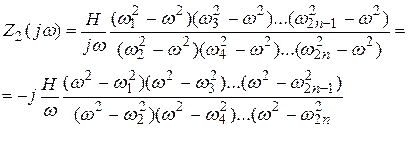
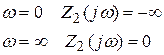
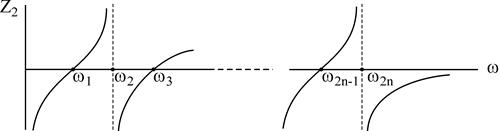
III класс.
знаменателя и Степени числителя отличаются на 1 (m=n+1).
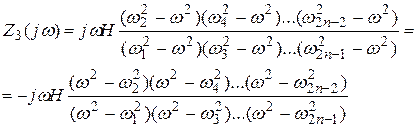
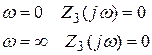
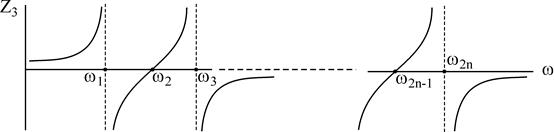
IV класс.
знаменателя и Степени числителя отличаются на 1 (n=m+1)
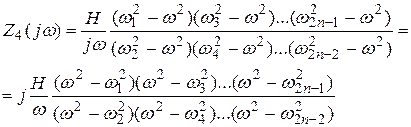
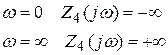
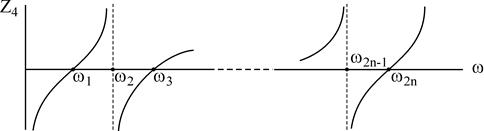
Частотные характеристики сопротивлений двухполюсников возможно изобразить посредством нулей (0) и полюсов (x).
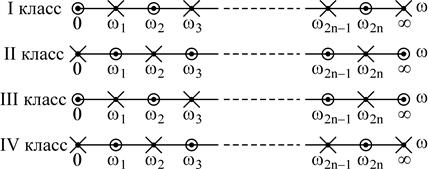
Выражениям входного сопротивления (Z1, Z2, Z3, Z4 (j?)) и входной проводимости (Y1, Y2, Y3, Y4 (j?)) соответствуют определенные схемы реактивных двухполюсников, каковые стали называться канонических схем.
Вероятны два варианта нахождения схем. Первый вариант основан на нахождении корней знаменателя и числителя и представлении выражений Z(j?) либо Y(j?) в виде (на примере Z4(j?), Y4(j?)):
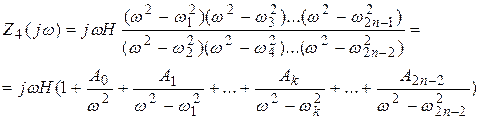
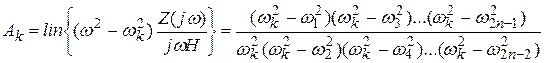
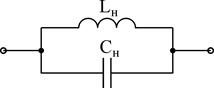
Таким же образом возможно разглядеть проводимости. В следствии анализа выражений и такого представления Z(j?) и Y(j?) приобретаем, что каждому классу соответствуют две схемы (схемы Фостера):
1)
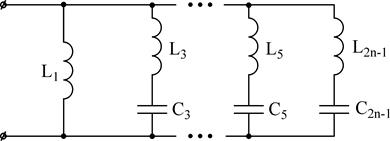
2)
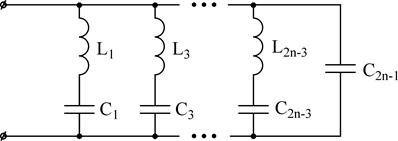
3)
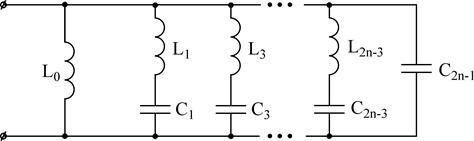
4)
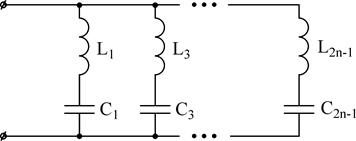
Одновременно с этим для схем двухполюсников вида
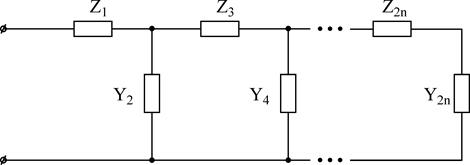
проводимость и Входное сопротивление возможно представить в виде цепочечной дроби (схемы стали называться цепных либо лестничных).
В случае, если канонические выражения входных сопротивлений (Z1, Z2, Z3, Z4 (j?)) и проводимостей (Y1, Y2, Y3, не4 (j?)) представить в виде цепочечной дроби возможно взять еще по два варианта канонических схем каждого класса (схемы Кауэра):
1)
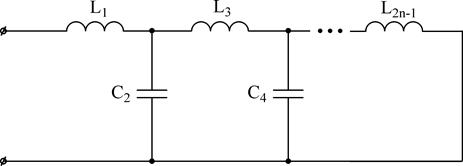
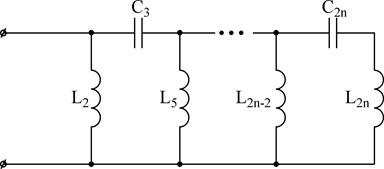
2)
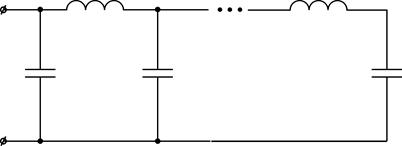
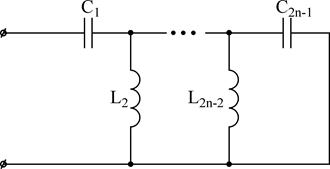
3)
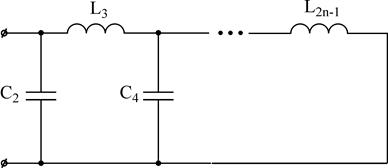
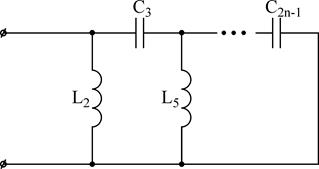
4)
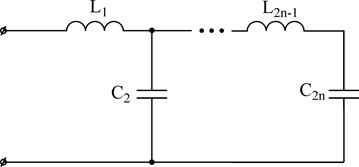
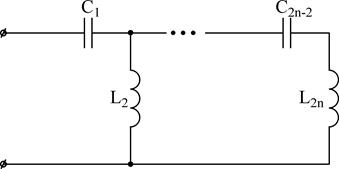
Любая из четырех схем соответствующего класса имеет уже продемонстрированную выше амплитудо-частотную чёрта (т.е. в каждом классе схем – 4, направляться – 1).