Экспериментальное получение таблицы истинности логического элемента 2И-НЕ, составленного из элементов 2И и НЕ
1. Соберите схему, изображенную на рис. 2.
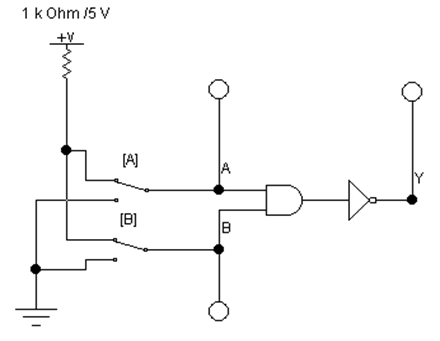
Рис. 2
2. Включите схему.
3. Подайте на входы схемы все вероятные комбинации уровней входных сигналов, замечая уровни сигналов на выходе и входах посредством логических пробников.
4. Заполните таблицу истинности логической схемы 2И-НЕ (табл. 6).
Экспериментальное получение таблицы истинности логического элемента 2И-НЕ
1. Соберите схему, изображенную на рис. 3.
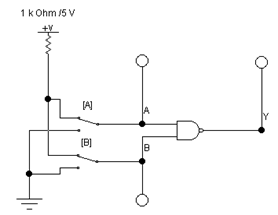
Рис. 3
2. Включите схему.
3. Подайте на входы схемы все вероятные комбинации уровней входных сигналов замечая уровни сигналов на выходе и входах посредством логических пробников.
4. Заполните таблицу истинности логической схемы 2И-НЕ (табл. 7).
5. Сравните табл. 6 и 7 между собой.
Опыт 3. Изучение логической функции Либо
Экспериментальное получение таблицы истинности логического элемента Либо
1. Соберите схему по рис. 4
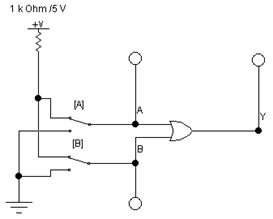
Рис. 4
2. Включите схему.
3. Подайте на входы схемы все вероятные комбинации уровней входных сигналов, замечая уровни сигналов на выходе и входах посредством логических пробников.
4. Заполните таблицу истинности логической схемы Либо (табл. 8).
Опыт 4. Изучение логической функции ИЛИ-НЕ
Экспериментальное получение таблицы истинности логического элемента 2ИЛИ-НЕ, составленного из элементов 2Либо и НЕ
1. Соберите схему, изображенную на рис. 5.
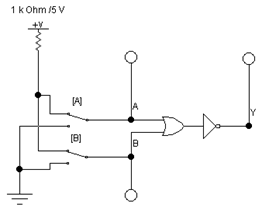
Рис. 5
2. Включите схему.
3. Подайте на входы схемы все вероятные комбинации уровней входных сигналов и, замечая уровни сигналов на выходе и входах посредством логических пробников, заполните таблицу истинности логической схемы 2ИЛИ-НЕ (табл. 9).
Экспериментальное получение таблицы истинности логического элемента 2ИЛИ-НЕ
1. Соберите схему, изображенную на рис. 6.
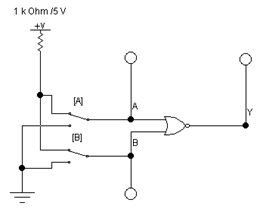
Рис. 6
2. Включите схему.
3. Подайте на входы схемы все вероятные комбинации уровней входных сигналов, замечая уровни сигналов на выходе и входах посредством логических пробников.
4. Заполните таблицу истинности логической схемы 2ИЛИ-НЕ (табл. 10).
5. Сравните табл. 9 и 10 между собой.
Опыт 5. Изучение логических схем посредством
генератора слов
Сведения об исследуемой микросхеме
1. Соберите схему, изображенную на рис. 7.
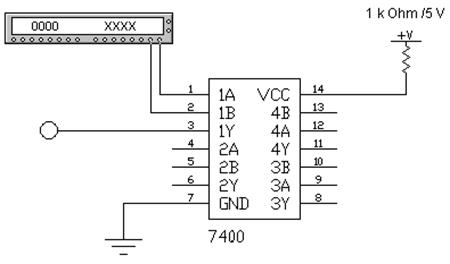
Рис. 7
2. Включите схему.
3. Укажите, к каким выводам микросхемы 7400 подключается источник питания, сколько элементов 2И-НЕ содержит микросхема, сколько элементов употребляется в данном опыте и как обозначены на схеме применяемые выходы и входы.
4. Заполните таблицу сведений о микросхеме (табл. 11).
Экспериментальное получение таблицы истинности логического элемента 2И-НЕ
1. Запрограммируйте генератор слов так, дабы на выходе генератора приобретать последовательно следующие комбинации: 00, 01, 10, 11.
2. Переведите генератор в режим пошаговой работы нажатием кнопки «Step» на увеличенном изображении генератора. Каждое нажатие кнопки «Step» приводит к переходу к очередному слову заданной последовательности, которое подается на выход генератора.
3. Последовательно подавая на микросхему слова из заданной последовательности, заполните таблицу истинности элемента 2И-НЕ (табл. 12).
Указание: значения разрядов текущего слова на выходе генератора отображаются в круглых окнах в нижней части на панели генератора.
их обработка и Результаты экспериментов
Опыт 1
Таблица 4
| Напряжение на входе В (ключ в нижнем положении), В | Логический сигнал на входе В (ключ в нижнем положении) | Напряжение на входе В (ключ в верхнем положении), В | Логический сигнал на входе В (ключ в верхнем положении) | Логический сигнал на выходе Y |
Таблица 5
| Входы | Выход | |
| А | В | Y |
Опыт 2
Таблица 6 Таблица 7
| Входы | Выход | Входы | Выход | ||
| А | В | Y | А | В | Y |
Опыт 3
Таблица 8
| Входы | Выход | |
| А | В | Y |
Опыт 4
Таблица 9Таблица 10
| Входы | Выход | Входы | Выход | ||
| А | В | Y | А | В | Y |
Опыт 5
Таблица 11Таблица 12
| Число элементов И-НЕ в микросхеме | Входы | Выход | ||
| Число исследуемых элементов 2И-НЕ | А | В | Y | |
| Обозначение выводов для подключения источника питания | ||||
| Обозначение применяемых входов | ||||
| Обозначение применяемого выхода |
Вопросы к защите
1. Может ли быть логическим знаком уровень напряжения? Состояние контакта? Свечение светодиода?
2. Датчик температуры складывается из контакта, что замыкается (размыкается) при превышении заданной температуры. При замыкании контакта вырабатывается сигнал логической единицы, при размыкании — логического нуля. Какую схему направляться применять для обнаружения срабатывания хотя бы одного датчика пожарной сигнализации:
а) при увеличении температуры в датчике происходит замыкание контакта;
б) при увеличении температуры в датчике происходит размыкание контакта?
3. Какой сигнал должен быть подан на неиспользуемый вход элемента 4ИЛИ-НЕ при реализации функции 3ИЛИ-НЕ?
4. Какой сигнал должен быть подан на неиспользуемые входы элемента 8И-НЕ при реализации функции 5И-НЕ?
5. В вашем распоряжении имеются логические элементы 2И-НЕ. Как на их базе сделать схему 3И? Достаточно ли четырех элементов 2И-НЕ для исполнения данной задачи?
6. Как будет вести себя схема И, в случае, если на одном из входов благодаря внутренней неисправности будет всегда присутствовать логическая единица? Логический нуль? Составьте таблицу истинности для неисправной схемы 3И. Выясните поведение схемы И-НЕ при тех же условиях.
7. Как будет вести себя схема Либо, в случае, если на одном из входов благодаря внутренней неисправности будет всегда присутствовать логическая единица? Логический нуль? Составьте таблицу истинности для неисправной схемы 3Либо. Выясните поведение схемы ИЛИ-НЕ при тех же условиях.
Перечень литературы:
1. Карлащук В. И. Электронная лаборатория на IBM PC. Программа Electronic Workbench и ее использование. М.: Солон-Р, 2000. С. 125-133, 218-226.
2. Касаткин А. С., Немцов М. В. Электротехника: учебник. М.: Высш. шк., 2000. С. 306-311.
3.Панфилов Д. И., Иванов В. С., Чепурин И. Н. электроника и Электротехника в упражнениях и экспериментах. Практикум на Electronic Workbench. М.: Изд-во «Додэка», 1999. Т1. С. 219-234.
Лабораторная работа №12
Цифровые автоматы с памятью
Цель
Изучение алгоритмов и структуры работы асинхронных и синхронных триггеров, возбуждения функций и исследование переходов главных типов триггеров, изучение взаимозаменяемости триггеров разных типов.
Домашнее задание
1. Чем отличается работа RS-триггера с прямыми входами от работы RS-триггера с инверсными входами?
2. По какой причине Т-триггер стал называться счетного? Какое число импульсов он может сосчитать?
3. По какой причине при подключении счетных входов триггеров к инверсным входам прошлых каскадов на D-триггерах он трудится как суммирующий, а при подключении к прямым — как вычитающий?
Краткие сведения из теории
Триггер — несложная цифровая схема последовательностного типа.
Состояние выхода последовательностной схемы (цифрового автомата) зависит еще и от внутреннего состояния схемы Q: Y=F(X,Q).
Иначе говоря цифровой автомат есть не только преобразователем, но и хранителем предшествующей и источником текущей информации (состояния). Это свойство обеспечивается наличием в схемах обратных связей.
Базой последовательностных схем являются триггеры. Триггер имеет два устойчивых состояния: Q=1 и Q=0, исходя из этого его время от времени именуют бистабильной схемой. В каком из этих состояний окажется триггер, зависит от сигналов на входах триггера и от его прошлого состояния, т. е. он имеет память. Возможно заявить, что триггер есть элементарной ячейкой памяти.
Тип триггера определяется методом его работы. В зависимости от метода работы триггер может иметь установочные, информационные и управляющие входы. Установочные входы устанавливают состояние триггера независимо от состояния вторых входов. Входы управления разрешают запись данных, подающихся на информационные входы. Самый распространенными являются триггеры RS, JK, D и Т-типов.
RS-триггер — несложный автомат с памятью, что может быть в двух состояниях. Триггер имеет два установочных входа: установки S (set -установка) и сброса R (reset — сброс), на каковые подаются входные сигналы от внешних источников. При подаче на вход установки активного логического уровня триггер устанавливается в 1 (Q = 1, Q = 0), при подаче активного уровня на вход сброса триггер устанавливается в 0 (Q = О, Q = 1). В случае, если подать на оба входа установки (возбуждения) пассивный уровень, то триггер будет сохранять прошлое состояние выходов: Q=0 (Q = 1) или Q=1 (Q = 0). Каждое состояние устойчиво и поддерживается за счет действия обратных связей.
Для триггеров этого типа есть недопустимой одновременная подача активного уровня на оба входа установки, т. к. триггер по определению не имеет возможности в один момент быть установлен в единицу и ноль. На практике подача активного уровня на установочные входы ведет к тому, что это состояние не может быть сохранено и нереально выяснить, в каком состоянии будет пребывать триггер при последующей подаче на установочные входы сигналов пассивного уровня.
На рис. 1 и 2 продемонстрированы два вида RS-триггеров, выполненных на элементах ИЛИ-НЕ и И-НЕ.
Для схемы на рис. 1 активным уровнем есть уровень логической единицы, для схемы на рис. 2 — уровень логического нуля. Схема (рис. 2) стала называться RS-триггера с инверсными входами — RS-триггер.
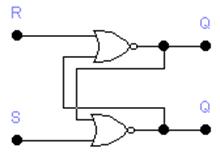
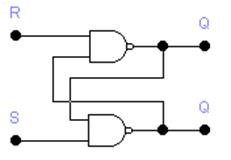
Рис. 1 Рис. 2
RS-триггер есть главным узлом для построения последовательностных схем. Наименование схем для того чтобы типа «последовательностные» свидетельствует, что состояние выхода зависит от того, в какой последовательности на входы подаются входные комплекты и каково было предшествующее внутреннее состояние. Так, в случае, если в RS-триггере (рис. 1) сначала установить комбинацию R=0, S=1 (сокращенная запись — 01), а позже перейти к R=0, S=0 (00), то состояние выхода Q=1. В случае, если же сначала установить комбинацию 10, а позже перейти к 00, то состояние выхода будет вторым — Q=0, не обращая внимания на однообразные комбинации сигналов на входах. Так, при одном и том же входном комплекте 00 выход триггера может быть в различных состояниях.
Условия переходов триггеров из одного состояния в второе (метод работы) возможно обрисовать табличным, аналитическим либо графическим методами. Табличное описание работы RS-триггера (рис. 1) представлено в табл. 1 (таблица переходов) и табл. 2 (таблица функций возбуждения).
Таблица 1 Таблица 2
| R | S | Qt+1 | Qt | Qt+1 | R | S | |
| Qt | x | ||||||
| — | x |
В таблицах использованы следующие обозначения:
Qt — предшествующее состояние выхода;
Qt+i- новое состояние, устанавливающееся по окончании перехода (допустимо Qt+i= Qt);
х — равнодушное значение сигнала: 0 либо 1;
— — неизвестное состояние.
Аналитическое описание (характеристическое уравнение) возможно взять из табл. 1, 2 правильно алгебры логики:
.
Зависимость Qt+1от Qtхарактеризует свойство запоминания предшествующего состояния.
Триггер JK-типа имеет более сложную, если сравнивать с РS-триггером, структуру и более широкие функциональные возможности. Кроме информационных входов J и К и прямого и инверсного выходов Q и Q1, JK-триггер имеет вход управления С (данный вход кроме этого именуют тактирующим либо счетным), и асинхронные установочные R- и S-входы. В большинстве случаев активными уровнями установочных сигналов являются нули, как в схеме на рис. 2. Установочные входы имеют приоритет над остальными. Деятельный уровень сигнала на входе 8 устанавливает триггер в состояние Q=1, а деятельный уровень сигнала на входе R — в состояние Q=0, независимо от сигналов на остальных входах.
В случае, если на входы установки в один момент подать пассивный уровень сигнала, то состояние триггера будет изменяться по фронту импульса на счетном входе в зависимости от состояния входов J и К, как продемонстрировано в таблицах переходов (табл. 3) и функций возбуждения (табл. 4).
Таблица 3 Таблица 4
| J | K | Qt+1 | Qt | Qt+1 | J | K | |
| Qt | x | ||||||
| Qt | x |
Работа JK-триггера описывается характеристическим уравнением Qt+1=JtQt v QtKt.
Один из вариантов функциональной схемы JK-триггера со входами установки логическим нулем и его условное графическое обозначение (УГО) приведены на рис. 3, 4. Временные диаграммы его работы при R=S=1 приведены на рис. 5.
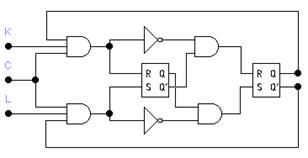
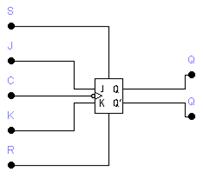
Рис. 3 Рис. 4
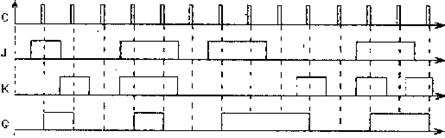
Рис. 5
Подобно RS-триггеру, изменение состояний JK-триггера возможно изобразить графом переходов (рис. 6). Входные сигналы, каковые смогут принимать каждые значения (как 0, так и 1), обозначены как X, а позиция обозначения соответствует последовательности J, К.
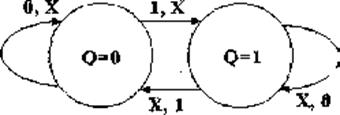
Рис. 6
Данный рисунок не должен вводить в заблуждение: в случае, если Х=1, то при JK=11 схема будет переходить из состояния Q=0 в состояние Q=1. Но из этого состояния схема обязана возвратиться в Q=0 и т. д. Данный граф обрисовывает работу автогенератора.
В этом случае все трансформации выхода происходят лишь в момент отрицательного перепада тактового сигнала С. Вправду, в случае, если J=K=1, то с каждым новым тактовым импульсом выход будет изменять собственный значение на противоположное и триггер будет делать функцию делителя частоты на 2, а не автогенератора.
D-триггер имеет один информационный вход D (data — эти). Информация со входа D заносится в триггер по хорошему перепаду импульса на счетном входе С и сохраняется до следующего хорошего перепада на счетном входе триггера. Кроме счетного С и информационного D входов, триггер снабжен асинхронными установочными R и S входами. Установочные входы приоритетны. Они устанавливают триггер независимо от сигналов на входах С
и D. Функционирование D-триггера описывается таблицей переходов (табл. 5), таблицей функций возбуждения (табл. 6) и диаграммами входных и выходных сигналов (рис. 7).
Таблица 5 Таблица 6
| D | Qt+1 | Qt | Qt+1 | D | |
Характеристическое уравнение D-триггера:
Qt+1=Dt.
Уравнение говорит о том, что состояние триггера на (t+1)-такте равняется входному сигналу в момент, предшествующий тактовому перепаду сигнала С. Условное обозначение D-триггера представлено на рис. 8.
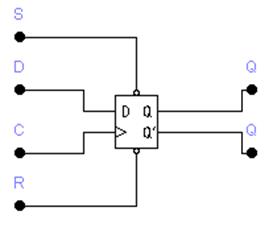
Рис. 8
Функциональная схема D-триггера возможно взята из схемы JK-триггера методом подключения входа К ко входу J через инвертор: D=J=K.
На базе JK-триггеров и D-триггеров возможно выстроить схемы, осуществляющие так называемый счетный режим. Такие схемы именуют Т-триггерами либо счетными триггерами, связывая с этим метод их функционирования. На рис. 9 представлены схемы организации Т-триггера на базе JK- и
D-триггеров. Счетный режим иллюстрируется временными диаграммами на рис. 10.
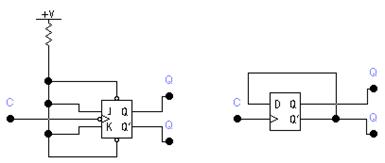
Рис. 9
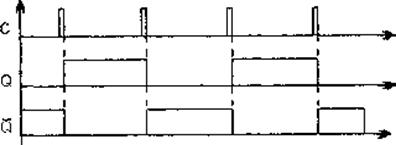
Рис. 10
В JK-триггере со входами установки логическим нулем счетный режим реализуется методом подачи констант J=K=1 и R=S=1 и входного сигнала Т на вход С. В соответствии с таблицей функционирования (табл. 3 и 4) при каждом отрицательном перепаде входного сигнала Т состояние триггера изменяет собственный значение на противоположное.
В D-триггере счетный режим реализуется при помощи обратной связи (на вход D подается сигнал с инверсного выхода). Так, постоянно существует неравенство сигнала на входе D и сигнала на выходе Q: в случае, если Q=1, D=0. Следовательно, при каждом хорошем перепаде сигнала на счетном входе С, в соответствии с принципом действия D-триггера, состояние выхода будет изменяться на противоположное.
Так, на каждые два входных тактовых импульса Т-триггер формирует один период выходного сигнала Q. Следовательно, триггер осуществляет деление частоты fTна его входе на 2:
fQ=fT/2,
где fQ— частота следования импульсов на выходе триггера.
Счетчик — устройство для подсчета числа входных импульсов. Число, воображаемое состоянием его выходов по фронту каждого входного импульса, изменяется на единицу. Счетчик возможно реализовать на нескольких триггерах. В суммирующих счетчиках любой входной импульс увеличивает число на его выходе на единицу, в вычитающих счетчиках любой входной импульс сокращает это число на единицу. самые простые счетчики — бинарные. На рис. 11представлен суммирующий диаграммы и двоичный счётчик его работы.
Как уже говорилось ранее, счетчики возможно реализовать на триггерах. Наряду с этим триггеры соединяют последовательно. Выход каждого триггера конкретно действует на тактовый вход следующего. Чтобы реализовать суммирующий счетчик, нужно счетный вход очередного триггера подключать к инверсному выходу прошлого. Чтобы поменять направление счета (реализовать вычитающий счетчик), возможно предложить следующие методы:
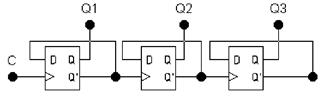 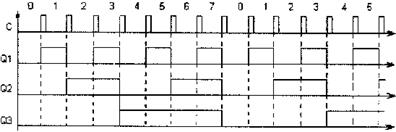 Рис. 11 |
1. Считывать выходные сигналы счетчика не с прямых, а с инверсных выходов триггеров. Число, образуемое состоянием инверсных выходов триггеров счетчика, связано с числом, грамотным состоянием прямых выходов триггеров следующим соотношением:
NПР= 2n- NИHB- l,
где n — разрядность выхода счетчика. В табл. 11 приведен пример связи числа на прямых выходах с числом на инверсных выходах триггеров счетчика.
2. Поменять структуру связей в счетчике: подавать на счетный вход следующего триггера сигнал не с инверсного, а с прямого выхода прошлого, как продемонстрировано на рис. 12. В этом случае изменяется последовательность переключения триггеров.
Таблица 11
| Состояние прямых входов | Число | Состояние инверсных входов | Число | ||||
| Q3 | Q2 | Q1 | N | Q3’ | Q2’ | Q1’ | N |
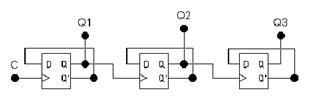
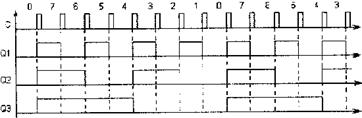
Рис. 12
Счетчики характеризуются числом состояний в течение одного периода (цикла). Для схем на рис. 11 и 12 цикл содержит N = 23= 8 состояний (от 000 до 111). Довольно часто число состояний именуют коэффициентом пересчета Ксч, что равен отношению числа импульсов nc на входе к числу импульсов на выходе старшего разряда за период:
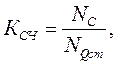
В случае, если на вход счетчика подавать периодическую последовательность импульсов с частотой fc, то частота Fq на выходе старшего разряда счетчика будет меньше в Ксч раз.
Исходя из этого счетчики кроме этого именуют делителями частоты, а величину Ксч — коэффициентом деления. Для повышения величины Ксч приходится повышать колличество триггеров в цепочке. Любой дополнительный триггер удваивает число состояний и число счётчика Ксч. Для уменьшения коэффициента Ксч возможно в качестве выхода счетчика разглядывать выходы триггеров промежуточных каскадов. К примеру, для счетчика на трех триггерах Ксч=8, в случае, если забрать выход второго триггера, то Ксч=4. Наряду с этим Ксч есть целой степенью числа 2: 2, 4, 8, 16 и т. д.
Возможно реализовать счетчик, для которого Ксч — любое целое число. К примеру, для счетчика на трех триггерах возможно сделать Ксч от 2 до 7, но наряду с этим один либо два триггера смогут быть лишними. При применении всех трех триггеров возможно взять Ксч =5-7: 22 Ксч
Для построения суммирующего счетчика с Ксч=5 нужно, дабы по окончании формирования последнего числа из последовательности {0, 1, 2, 3, 4} счетчик переходил не к числу 5, а к числу 0. В бинарном коде это указывает, что от числа 100 необходимо перейти к числу 000, а не 101. Изменение естественного порядка счета допустимо при введении дополнительных связей между триггерами счетчика. Возможно воспользоваться следующим методом: когда счетчик попадает в нерабочее состояние (в этом случае 101), данный факт должен быть опознан и повлечь последующую выработку сигнала, что перевел бы счетчик в состояние 000. Разглядим данный метод более подробно.
Факт попадания счетчика в нерабочее состояние описывается логическим уравнением
Состояния 110 и 111 кроме этого являются нерабочими и исходя из этого учтены при составлении уравнения. В случае, если на выходе эквивалентной логической схемы F = 0, значит счетчик находится в одном из рабочих состояний: 0v1v2v3v4. Когда он попадает в одно из нерабочих состояний 5v6v7, формируется сигнал F = 1. Появление сигнала F = 1 должно переводить счетчик в начальное состояние 000, следовательно, данный сигнал необходимо применять для действия на установочные входы триггеров счетчика, каковые осуществляли бы сброс счетчика в состояние Qi = Qg = Qs = 0. При реализации счетчика на триггерах со входами установки логическим нулем для сброса триггеров требуется подать на входы сброса сигнал направляться=0. Для обнаружения факта попадания в нерабочее состояние используем схему, реализующую функцию F и выполненную на элементах И-НЕ. Для этого преобразуем выражение для функции
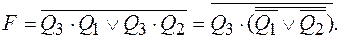
Соответствующая схема реализации приведена на рис.13.
Счетчик будет трудиться следующим образом: при счете от 0 до 4 все происходит как в простом суммирующем счетчике с Ксч =8. Установочные сигналы равны 1 и естественному порядку счета не мешают. Счет происходит по хорошему фронту импульса на счетном входе С. В тот момент, в то время, когда счетчик будет в состоянии 4 (100), следующий тактовый импульс сперва переводит счетчик в состояние 5 (101), что срочно (задолго до прихода следующего тактового импульса) ведет к формированию сигнала сброса, что поступает на установочные входы сброса триггеров. В следствии счетчик сбрасывается в 0 и ожидает прихода следующего тактового импульса на счетный вход. Один цикл счета закончился, счетчик готов к началу следующего цикла.
Используя такие схемы с обратной связью для сброса счетчика, необходимо иметь в виду, что операция сброса занимает конечное время, исходя из этого перед сбросом счетчика в 0 на выходе первого триггера появляются краткосрочные импульсы, либо «иголки». Это не имеет значения при подключении счет-
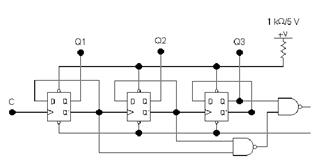
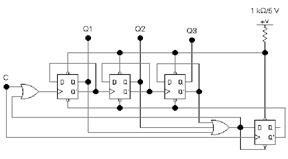
Рис. 13 Рис. 14
чика напрямую к индикатору, но при 1 пользовании этого выхода счетчика в качестве источника тактовых импульсов смогут появиться определенные неприятности. Схема, в которой это явление устранено, приведена на рис. 14. Ответственным отличием есть то, что схема обнаруживает не факт попадания в нерабочее состояние 101, а факт попадания в состояние 100 и в следующем такте производит сигнал сброса.
Рабочее задание