При ответе некоторых задач термодинамики появляется необходимость определения трансформации энтропии в ходе. Базой для вычисления есть уравнение (38)
 . |
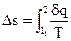Элементарное количество теплоты определяют по формуле (53)
| . |
Тип теплоёмкости в этом выражении определяется типом процесса
Изменение энтропии в изохорном ходе
В этом случае
| . |
Тогда
 . |
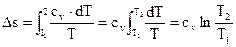(124) |
Изменение энтропии в изобарном ходе
В этом случае
| . |
 . |
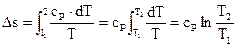(125) |
Изменение энтропии в изотермическом ходе
В этом случае элементарное количество теплоты равняется элементарной работе (см. выражение (100))
| . |
Тогда
 . |
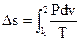(127) |
Из уравнения состояния совершенного газа возможно взять
.
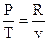Подставляя это выражение в (126), возьмём
 . |
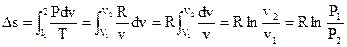(128) |
Изменение энтропии в направляться ходе
В этом случае
| . |
Тогда
 . |
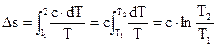(129) |
ЛЕКЦИЯ 11
Фазовые диаграммы
Фазой именуется состояние вещества, характеризующееся тем, что оно занимает определённую область пространства, и в пределах это области свойства и параметры вещества или остаются постоянными, или изменяются непрерывно. Эта пространственная область отделена от вторых частей пространства границей. Масса вещества, содержащегося в одной фазе, с течением времени может изменяться. В этом случае говорят о фазовом переходе. Фазовый переход осуществляется через границу раздела фаз. Выделяют следующие самый распространённые фазовые переходы:
кипение (переход вещества из жидкости в пар);
конденсация (переход вещества из пара в жидкость);
кристаллизация, затвердение (переход вещества из жидкости в жёсткое состояние);
плавление (переход вещества из жёсткого состояния в жидкость).
Фазы комфортно изображать на фазовых диаграммах. Фазовая диаграмма — это плоскость с веденной на ней декартовой совокупностью координат, по осям которой откладываются значения пары главных термодинамических параметров. Эта плоскость разбивается на последовательность областей, любая из которых воображает некую фазу. На фазовой диаграмме кроме этого представлены главные изолинии (линии постоянства главных термодинамических параметров: изохоры, изобары, изотермы, изоэнтропы, изоэтальпы и линии постоянной сухости.
Самый распространёнными являются фазовые диаграммы вида T-S, P-V, H-S, H-lgР. Разглядим фазовую T-S диаграмму. На рис. 31 продемонстрированы границы раздела и основные фазы фаз:
 |
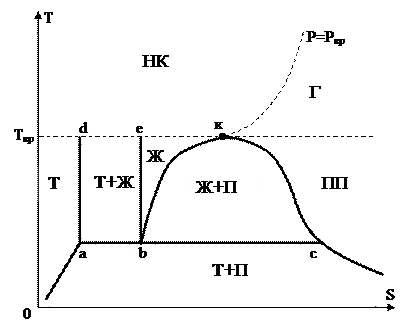Рис. 31.
Ж — жидкость
Ж + Т- жидкость +тело
НК – надкритическая область
Г – область газаВП – мокрый пар
bkc – кривая насыщения. Характеризует насыщеноt состояние вещества.
bk – линия насыщенной жидкости. Насыщенная жидкость — это жидкое состояние вещества, характеризующееся тем, что подвод сколь угодно малого количества тепла ведет к интенсивному образованию пара.
kс – линия сухого насыщенного пара. Это газовое состояние вещества, характеризующегося тем, что сколь угодно малое охлаждение ведет к началу процесса конденсации.
abc — линия тройных точек. Тройная точка — это состояние вещества характеризующегося равновесным сосуществованием сходу трёх фаз: жёсткой, жидкой и газовой. Равновесие фаз характеризуется тем, что между фазами отсутствует фазовый переход. При неизменных внешних условиях равновесие фаз может сосуществовать какое количество угодно. Чтобы две фазы были в состоянии равновесия, нужно исполнение трёх условий: 1)фазы должны иметь однообразное давления; 2) фазы должны владеть однообразными температура; 3) фазы должны владеть химическим потенциалом.
be – линия начала процесса затвердевания либо окончания процесса плавления.
аd — линия окончания процесса затвердевания либо начала процесса плавления.
dek – изотерма критической температуры.
P=Pкр – критическая изобара.
k – критическая точка. Характеризуется тем, что при температуре, выше критической , нереально взять жидкость посредством изотермического сжатия. температура и Критическое давление – это давления и температура ниже критической точки.
Область Г – область газа. Эта область находится при давлении ниже критического, и температуре выше критической. Область газа характеризуется тем, что состояние газа в данной области описывается уравнением состояния совершенного газа.
Область ПП — область перегретого пара. Находится при температуре ниже критической и справа от линии kc. Эта область характеризуется тем, что в ней поведение вещества описывается уравнением Ван- дер- Ваальсом либо модифицированным уравнением совершенного газа
| , | (130) |
где z- коэффициент сжимаемости (поправочный коэффициент, учитывающий отклонение поведения настоящего веществ от совершенного газа).
Область Ж+П — область мокрого пара. Ограничивается кривой насыщения и линией тройных точек. Это двухфазная область, характеризуемая равновесным состоянием насыщенного пара и насыщенной жидкости. Эта область кипения процессов и протекания конденсации.
Область Ж. — область переохлажденной жидкости. Она ограничена сверху критической изотермой, справа — линией насыщенной жидкости, слева — линией начала кристаллизации.
Область Т+Ж — двухфазовая область равновесного сосуществования жидкой фазы и жёсткой. Эта область протекания процессов затвердевания (кристаллизации) плавления.
Область Т+П — двухфазовая область равновесного сосуществования насыщенного пара и жёсткого тела. Сверху эта область ограничена линией тройных точек. Тройной точкой именуется состояние равновесия сходу трёх агрегатных состояний. Эта область протекания процессов сублимации и десублимации. Сублимацией именуют процесс перехода жёсткой фазы в газообразную. Десублимацией именуют процесс перехода насыщенного пара в жёсткую фазу.
Область НК – область надкритического состояния вещества. Находится при температуре и давлении выше критических. Характеризуется тем, что вещество в этом состоянии владеет особенностями и жидкости, и газа.
На рис. 32 продемонстрированы линии главных процессов.
 |
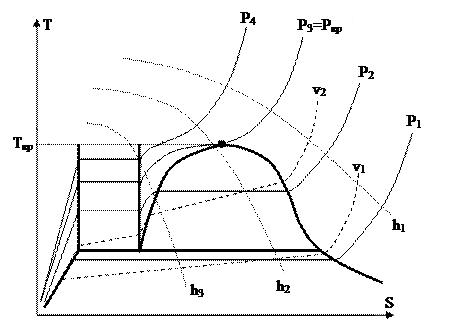Рис. 32.
Изобары, соответствующие давлениям Р1, Р2, Р3=Ркр и Р4, изображены целыми линиями. Наряду с этим между этими давлениями выполняются соотношения Р1
Изохоры в v1 и v2 (v1v2) изображённые штриховыми линиями, находятся в T-S диаграмме более сильно, чем изобары. направляться подчернуть, что в двухфазных областях изохоры не совпадают с изотермами, т.е. не горизонтальны.
Изоэнтальпы h1, h2 и h3 (h1h2h3) изображены пунктирными линиями. Возможно обратить внимание на то, что с понижением температуры угол наклона изоэнтальпы к оси S возрастает.
Мокрый пар
Мокрый пар – это состояние вещества, при котором находятся в равновесии насыщенная жидкость и насыщенный пар. Равновесие обусловлено равенством их давлений и температур. Область мокрого пара находит громаднейшее использование в теплоэнергетических и низкотемпературных устройствах, т.к. в данной области самый легко реализовать серьёзные в технических приложениях процессы (изотермический).
Область мокрого пара, изображённая в T-S диаграмме, представлена на рис. 33.
 |
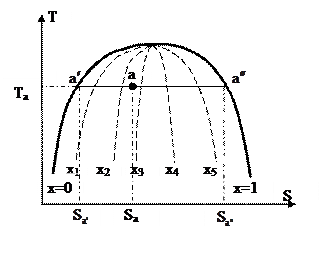Рис. 33.
Точка «а» характеризует состояние мокрого пара, при котором в определенных массовых долях находятся в равновесии насыщенный пар и насыщенная жидкость.
Насыщенный пар будет в состоянии , а состояние насыщенной жидкости характеризуется точкой . Пускай мокрый пар а в состоянии точки а занимает некий количество , где m- масса мокрого пара; va — удельный количество мокрого пара. Данный же количество возможно разглядывать как сумму количеств насыщенной жидкости и насыщенного пара
| , | (131) |
где — количество насыщенной жидкости;
— количество насыщенного пара;
— масса насыщенной жидкости;
— масса насыщенного пара;
— удельный количество насыщенной жидкости в состоянии точки ;
— удельный количество насыщенного пара в состоянии точки .
Наряду с этим разумеется соотношение
| , | (132) |
из которого, высказывая и подставляя полученное выражение в (131), возьмём
| . |
Дробя в последнем выражении обе части равенства на m, возьмём уравнение, высказывающее удельный количество мокрого пара через удельные количества насыщенной жидкости и насыщенного пара
| . | (133) |
В этом выражении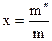 
— степень сухости мокрого пара, которая показывает массовую долю насыщенного пара во мокром паре. В случае, если x=1, то мокрый пар абсолютно складывается из насыщенного пара. В случае, если x=0, то мокрый пар абсолютно складывается из насыщенной жидкости. Степень сухости может принимать каждые значения из промежутка от 0 до 1. Совокупность всех точек области мокрого пара на T-S диаграмме, владеющие одним значением степени сухости, именуются линиями постоянной сухости (см. рис. 33).
Совершенно верно такими же рассуждениями, применяя энтропии аддитивности и свойство энтальпии, возможно взять выражения
| , | (134) |
| , | (135) |
где — удельная энтальпия насыщенной жидкости в состоянии точки ;
— удельная энтальпия насыщенного пара в состоянии точки ;
— удельная энтропия насыщенной жидкости в состоянии точки ;
— удельная энтропия насыщенного пара в состоянии точки .
Выразим из последнего уравнения х
 . |
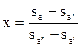(136) |
Из данной формулы направляться, что для повышения степени сухости, необходимо увеличивать энтропию , т.е. подводить теплоту к мокрому несколько. Наряду с этим часть насыщенной жидкости будет уменьшаться, а насыщенного пара возрастать. Параметры же насыщенной жидкости и насыщенного пара наряду с этим изменяться не будут. Таковой процесс именуется кипением. В случае, если отводить теплоту от мокрого пара, то энтропия будет уменьшаться, соответственно степень сухости будет понижаться, т.е. вещество будет переходить из состояния насыщенного пара в состояние насыщенной жидкости. Таковой процесс именуется конденсацией.
Чтобы 1 кг насыщенной жидкости абсолютно перевести в состояние сухого насыщенного пара, нужно подвести некое количество тепла, которое именуется удельной теплотой парообразования r, .
В изобарном ходе, которым являются кипение либо конденсация, подведенная либо отведенная теплота равна трансформации энтальпии. Исходя из этого справедливо соотношение
| . | (137) |
Учитывая сообщение теплоты с трансформацией энтропии в изотермическом ходе , возьмём
| . | (138) |
ЛЕКЦИЯ 12
Термодинамический цикл
Термодинамическим циклом именуется замкнутый термодинамический процесс, т.е. процесс, в следствии осуществления которого совокупность возвращается в исходное состояние. Возможно дать второе определение термодинамическому циклу как последовательности термодинамических процессов, исполнение которых приводит совокупность в исходное состояние. Запишем первый закон термодинамики для замкнутой совокупности в виде
.
Потому, что совокупность возвращается в исходное состояние, то . В следствии получается обобщённое уравнение термодинамического цикла
| , | (139) |
где Q — суммарная теплота, которой совокупность обменивается с окружающей средой;
L – совокупная работа, которую совокупность совершает либо затрачивает.
Теплоту Q возможно представить в виде
| , | (140) |
где Q1 — суммарная теплота, подведенная в цикле к совокупности;
Q2 — суммарная теплота, отведенная в цикле от совокупности.
Подставляя (140) в (139), возьмём
| . | (141) |
В этом выражении отведённая теплота берётся хорошей, т.к. символ отводимой теплоты учтён в формуле минусом перед Q2.
Уравнение (141)разрешает классифицировать термодинамические циклы на два вида:
1. в случае, если , то и цикл именуется прямым;
2. в случае, если , то и цикл именуется обратным.
Прямой цикл
Прямой цикл кроме этого именуют теплосиловым. Это цикл, в следствии осуществления которого совокупность создаёт, т.е. совершает, работу за счёт подводимого к совокупности тепла.
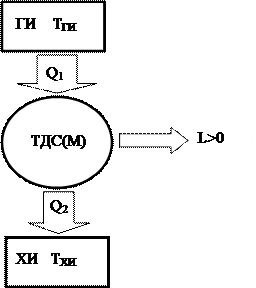Принципиальная схема устройства, реализующего прямой, либо теплосиловой, цикл представлена на рис. 34.
Рис. 34.
На этом рисунке:
ТДС(М) –термодинамическая совокупность (машина) которая совершает цикл;
ГИ – тёплый источник с температурой TГИ. Под ним понимается совокупность тел экологии, каковые передают теплоту Q1 термодинамической совокупности.
ХИ – холодный источник, либо холодильник, с температурой ТХИ. Это совокупность тел экологии, которым совокупность, совершая цикл, отдает теплоту Q2. Чтобы схема, представленная на рис. 34, могла быть реализована, холодный источник должен иметь температуру ТХИ ,меньшую, чем температура тёплого источника ТГИ (ТХИ
 |
 |
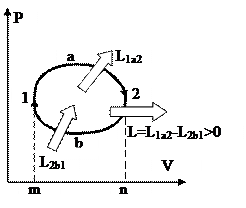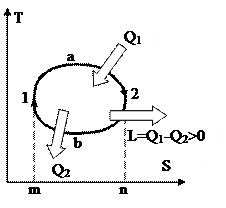
Рис. 35. Рис. 36.
На рис. 35 изображён теплосиловой цикл в Т-S диаграмме. Процесс 1а2 сопровождается подводом тепла Q1, т.к. энтропия возрастает. Наряду с этим подведённая теплота равна площади под линией 1а2. В ходе 2b1 теплота Q2 отводится, т.к. энтропия значительно уменьшается, и эта теплота равна площади под линией 2b1. Из рисунка видно, что площадь фигуры m1a2n больше площади m1b2n, исходя из этого Q1Q2, и данный цикл прямой. В итоге разность подведённой и отведённой теплот равна работе цикла, и равна площади цикла.
На рис. 36 изображён теплосиловой цикл в P-V диаграмме. Процесс 1а2 сопровождается совершением работы L1a2, т.к. количество в этом ходе возрастает. Наряду с этим совершённая работа равна площади под линией 1а2. В ходе 2b1 работа L2b1затрачивается, т.к. количество значительно уменьшается, и эта работа равна площади под линией 2b1. Из рисунка видно, что площадь фигуры m1a2n больше площади m1b2n, исходя из этого L1a2L2b1, и данный цикл прямой. В итоге, разность совершённой и затраченной работ равна работе цикла и равна площади, ограниченной циклом.
Любой цикл, и прямой и обратный, характеризует коэффициент эффективности что оценивает эффективность процесса преобразования энергии
 , |
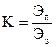(142) |
где K – коэффициент эффективности;
Эп – нужная энергия;
Ээ – затраченная энергия.
При прямого, либо теплосилового, цикла коэффициент эффективности именуется термическим коэффициентом нужного действия (КПД) и обозначается «?». Нужной энергией в теплосиловом цикле есть работа, а затраченной энергией есть подведённая теплота. В итоге выражение для термического КПД имеет форму
 . |
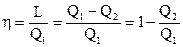(143) |
Т.к., в силу определения прямого цикла, , то КПД в любой момент меньше единице. Процесс преобразования тепловой энергии в нужную работу в цикле тем действеннее, чем ближе значение КПД цикла к единице.
Обратные циклы
Обратным именуется цикл, в котором подведённая теплота меньше отведённой . В итоге работа обратного цикла есть отрицательной, т.е. для его реализации нужно затратить работу.
Принципиальная схема устройства, реализующего обратный, цикл представлена на рис. 37.
 |
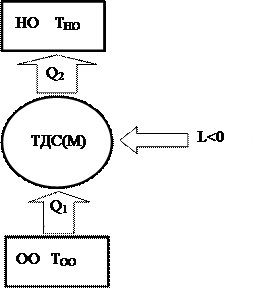Рис. 37.
На этом рисунке:
ОО — охлаждаемый объект с температурой ТОО;
НО – нагреваемый объект с температурой ТНО.
Наряду с этим, дабы в работе изображённой установки был суть, температура охлаждаемого объекта ТОО должна быть меньше температуры нагреваемого объекта ТНО. Для обратного цикла выполняется энергетический баланс
| . | (144) |
 |
 |
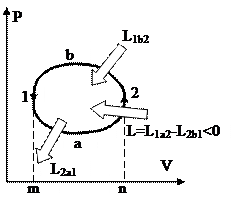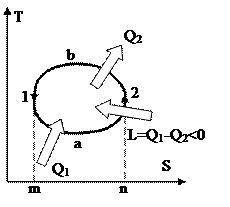
Рис. 38. Рис. 39.
На рис. 38 изображён обратный цикл в Т-S диаграмме. Процесс 1а2 сопровождается подводом тепла Q1, т.к. энтропия возрастает. Наряду с этим подведённая теплота равна площади под линией 1а2. В ходе 2b1 теплота Q2 отводится, т.к. энтропия значительно уменьшается, и эта теплота равна площади под линией 2b1. Из рисунка видно, что площадь фигуры m1a2n меньше площади m1b2n, исходя из этого Q1
На рис. 39 изображён обратный цикл в P-V диаграмме. Процесс 1а2 сопровождается совершением работы L1a2, т.к. количество в этом ходе возрастает. Наряду с этим совершённая работа равна площади под линией 1а2. В ходе 2b1 работа L2b1затрачивается, т.к. количество значительно уменьшается, и эта работа равна площади под линией 2b1. Из рисунка видно, что площадь фигуры m1a2n меньше площади m1b2n, исходя из этого L1a2
Обратные термодинамические циклы делятся на три вида:
1. холодильные циклы;
2. циклы теплового насоса;
3. комбинированные циклы.
Холодильный цикл изображён на рис. 40 под римской цифрой I. Это обратный цикл, в котором работа затрачивается чтобы отвести теплоту Q1 от охлаждаемого объекта, находящегося при температуре ТОО ниже температуры воздуха ТОС.
 |
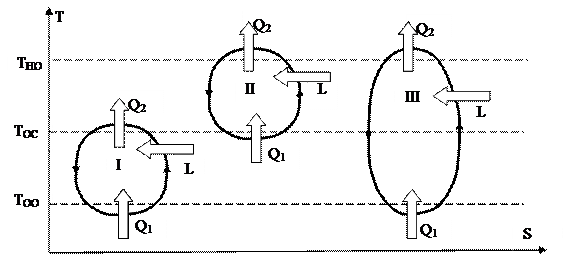Рис. 40.
Холодильные циклы реализуются в низкотемпературных установках, например, в бытовых холодильниках. В этом случае теплота Q1, подводимая к рабочему веществу (фреону), – это теплота, отводимая от продуктов, находящихся в морозильной камере.
Цикл теплового насоса II — это обратный цикл, в котором работа затрачивается для подвода тепла Q2 к нагреваемому объекту, находящемуся при температуре ТНО выше температуры воздуха ТОС. Это цикл реализуют бытовые кондиционеры, трудящиеся в режиме обогрева помещения. Нагреваемым объектом в этом случае есть комнатный воздушное пространство. Температура нагреваемого объекта — это комнатная температура. В качестве экологии выступает наружный воздушное пространство с низкой температурой. Теплота Q2, идущая на нагрев помещения в этом случае и определяемая по выражению (144), больше теплоты, которая подводилась бы при нагреве помещения электрическим нагревателем, в котором в тепловую энергию преобразовывается электроэнергия L.
Комбинированный цикл III – это обратный цикл, в котором работа затрачивается для отвода тепла Q1 от охлаждаемого объекта, находящемуся при температуре ТОО ниже температуры воздуха, и одновременному подводу тепла Q2 к нагреваемому объекту, находящемуся при температуре ТНО выше температуры воздуха. Устройством, реализующем комбинированный цикл, есть бытовой холодильник, находящийся в жилом помещении. Со своей стороны, с наружи этого помещения находится воздушное пространство с низкой температурой. В этом случае объектом нагрева, которому подводится теплота Q2 (отводимая от цикла), есть воздушное пространство , находящийся в помещении с комнатной температурой. Объектом охлаждения помогают продукты, находящиеся в морозильной камере, от которых отводится теплота Q1 и которая подводится к фреону, циркулирующему в холодильнике.
Коэффициент эффективности холодильного цикла именуется холодильным коэффициентом ?. Нужной энергий в этом случае есть теплота Q1, отводимая от охлаждаемого объекта и подводимая к рабочему веществу, совершающему цикл. Затраченной энергией есть подводимая работа L. Исходя из этого
 . |
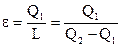(145) |
Из этого выражения видно, что, в отличие от КПД, холодильный коэффициент возможно как меньше, так и больше единицы. В этом его значительный недочёт, т.к. он не предоставляет эталона для сравнения (эталон для КПД – 1).
Коэффициент эффективности цикла теплого насоса именуется отопительным коэффициентом ?. В этом случае нужной энергией есть теплота Q2, подводимая к нагреваемому объекту (и отводимая от цикла). Затраченной энергией есть подводимая работа L. Исходя из этого
 . |
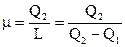(146) |
Из этого выражения видно, что отопительный коэффициент в любой момент больше единицы, причём цикл теплового насоса тем действеннее, чем большее значение принимает ? над единицей.
Коэффициент эффективности комбинированного цикла не имеет особого заглавия и обозначается k. Нужной энергий в этом случае есть теплота Q1, отводимая от охлаждаемого объекта, и в один момент теплота Q2, подводимая к нагреваемому объекту. Затраченной энергией есть подводимая работа L. Исходя из этого
 . |
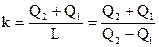(147) |
Из этого выражения видно, что коэффициент эффективности комбинированного цикла заведомо больше единицы,
ЛЕКЦИЯ 13
Обратимый цикл Карно
Все циклы, и прямые и обратные, делятся на 2 типа: обратимые и необратимые. Обратимым циклом именуется цикл, состоящий лишь из обратимых процессов. Необратимый цикл – это цикл, в котором присутствует хотя бы один необратимый процесс. Чтобы процесс был обратимый он должен быть равновесный, т.е. обязан протекать с нескончаемой малой скоростью. Это допустимо лишь в том случае, если разность потенциалов взаимодействующие с окружающей средой и системой будут вечно малыми. Для термодинамической совокупности это указывает, что при обратимом теплообмене с окружающей средой разность окружающей среды и температуры системы должна быть вечно малой величиной, т.е. должно отсутствовать термическое сопротивление между совокупностью и окружающее средой. сжатие и Обратимое расширение допустимо при вечно малой разности давления между окружающей средой и системой. Это допустимо лишь тогда, в то время, когда в совокупности отсутствует трение. Из этого направляться, что в термомеханической совокупности существует два источника необратимости:
1. наличие термического сопротивления между разными частями совокупности, что ведет к конечной разности температуры при теплообмене;
2. наличие трения в совокупности (или между окружающей средой и системой), которое ведет к конечной разности давлений.
Из всех термодинамических циклов обратимый цикл Карно (прямой) выделяют на том основании, что для заданной разности температур между горячим и холодным источниками обратимый цикл Карно имеет максимальный КПД.
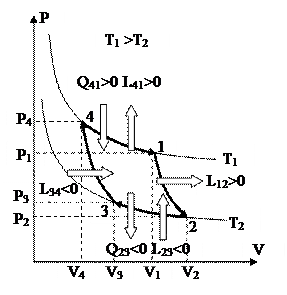
Обратимый цикл Карно, изображённый на рис. 41 и рис. 42, складывается из двух адиабат и двух изотерм.
 |
|||
 |
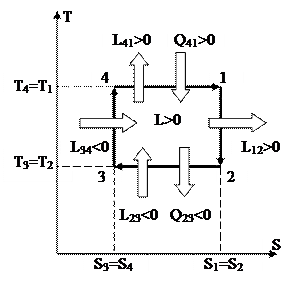Рис. 41. Рис. 42
1-2 – процесс адиабатного расширения. В этом ходе совершается работа L12.
2-3 – процесс изотермического сжатия. В этом ходе затрачивается работа L23 и отводится теплота Q23.
3-4 – процесс адиабатного сжатия. В этом ходе затрачивается работа L34.
4-1 – процесс изотермического расширения. В этом ходе совершается работа L41 и подводится теплота Q41.
Главными процессами цикла являются процессы 4-1 и 1-2. В них производится работа цикла. Остальные процессы являются запасными и направлены на то, дабы с мельчайшими затратами энергии вернуть совокупность в исходное состояние 4.
Определим КПД обратимого цикла Карно ?ОЦК:
По определению КПД (143)
 . |
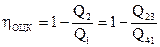(148) |
Теплоты Q23 и Q41 на базе (39) определяются выражениями
| , . |
Подставляя эти выражения в (148) и уменьшая на разность энтропий, возьмём
 . |
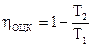(149) |
Потому, что разглядываемый цикл обратимый, то разность температур между горячим рабочим и источником веществом в ходе 4-1 будет вечно малой величиной. Исходя из этого
| . |
Исходя из тех же мыслей, возьмём
| . |
Подставив последние два соотношения в (149), возьмём выражение для КПД обратимого цикла Карно
 . |
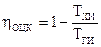(150) |
Это формула говорит о том, что КПД обратимого цикла Карно не зависит от особенностей рабочего тела, совершающего цикл Карно, и определяется лишь температурами тёплого и холодного источников. Данный вывод есть формулировкой первой теоремы Карно.