Часть 1.
Интеграл – одно из центральных понятий матанализа и всей математики, происхождение которого связано с двумя задачами: о восстановлении функции по её производной; о вычислении площади, заключенной между графиками функции на отрезке и осью абсцисс. Указанные две задачи приводят к двум видам интегралов: определённому и неизвестному.
На протяжении развития математики и под влиянием потребностей естествознания и техники понятие неопределённого и определённого интеграла подвергались последовательности изменений и обобщений.
Неизвестный интеграл – совокупность всех первообразных на промежутке функции : . В соответствии с главной теореме интегрального исчисления, для каждой постоянной на отрезке функции существует на соответствующем промежутке первообразная и, следовательно, неизвестный интеграл. В случае, если — одна из первообразных функции на , то , где — произвольная постоянная.
направляться подчернуть, что тут множество значений связное. На несвязном множестве неверно утверждение о том, что все первообразные постоянной функции отличаются на константу. Так равенство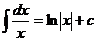 
, разглядываемое на объединении лучей , по большому счету говоря, неверно. К примеру, на этом множестве первообразными функции 
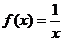являются функции 
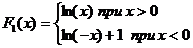и . Их разность 
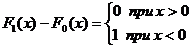не есть константой.
Определённый интеграл. Понятие определённого интеграла вводится как предел интегральных сумм. Для постоянной на отрезке функции понятие определённого интеграла в первый раз было введено Коши в его работе 1823 года: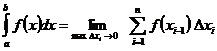 
для разбиений . Это частный случай определённого интеграла Римана (1853г.). Значительное продвижение в теории определённого интеграла в собственности Дарбу, что ввёл наровне с интегральной суммой Римана верхнюю и нижнюю суммы (1879г.). Нужное и достаточное условие интегрируемости по Риману разрывных функций установлено в 1902г. Лебегом.
Между определённым интегралом от постоянной на отрезке функции и неизвестным интегралом (другими словами первообразной) данной функции существует следующая сообщение:
1) В случае, если — каждая первообразная функции , то честна формула Ньютона-Лейбница:
;
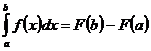2) Для любого неизвестный интеграл постоянной функции записывается в виде:
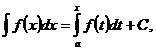
где – произвольная постоянная. В частности, определённый интеграл с переменным верхним пределом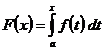 
представляет собой первообразную функцию .
Определённый интеграл Лебега. Для введения определённого интеграла от функции в смысле Лебега разбивают множество значений на частичные отрезки точками и обозначают через множество всех значений , для которых , а через – меру множества в смысле Лебега. Интегральную сумму Лебега функции на отрезке определяют равенством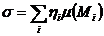 
, где – любое число из отрезка .
Функцию именуют интегрируемой в смысле Лебега на отрезке , в случае, если существует предел её интегральных сумм при рвении к нулю . Другими словами в случае, если существует такое число , что для любого найдется такое, что при единственном условии справедливо неравенство . Наряду с этим указанный предел именуют определённым интегралом Лебега от функции по отрезку .
Вместо отрезка логично разглядывать произвольное множество, измеримое довольно некоей неотрицательной полной счётно-аддитивной меры. Допустимо и второе определение интеграла Лебега, в то время, когда данный интеграл первоначально определяют на множестве так называемых несложных функций (другими словами измеримых функций, принимающих не более счётного множества значений), а после этого посредством операции предельного перехода расширяют понятие интеграла для произвольной функции, являющейся предел равномерно сходящейся последовательности несложных функций (равномерной сходимости достаточно практически везде).
Любая интегрируемая в смысле Римана функция ограничена и интегрируема в смысле Лебега. Обратное утверждение неверно, потому что существуют разрывные на множестве хорошей меры и вместе с тем ограниченные интегрируемые в смысле Лебега функции (к примеру, функция Дирихле.) Для интегрируемости по Лебегу ограниченной функции нужно и достаточно, дабы эта функция принадлежала классу измеримых функций. Функции, видящиеся в матанализе, в большинстве случаев, измеримы. Это указывает, что интеграл Лебега владеет общностью, исчерпывающей потребности анализа.
Интеграл Лебега охватывает и все случаи полностью сходящихся несобственных интегралов.
Несобственный интеграл – интеграл от неограниченной функции либо от функции по неограниченному множеству. Пускай функция выяснена на конечном либо нескончаемом полуинтервале , , и для любого , функция интегрируема по Риману (по Лебегу) на отрезке . Несобственным интегралом именуют
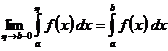
(при условие ). В случае, если предел существует, то говорят, что несобственный интеграл сходится, если не существует – расходится. К примеру, несобственный интеграл:
, ,
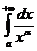сходится при , а при расходится. В случае, если же , то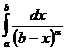 
сходится при и расходится при .
В случае, если и функция интегрируема по Риману (по Лебегу) на отрезке , то несобственный интеграл совпадёт с определённым интегралом. Подобно при соответствующих догадках определяют несобственный интеграл по промежутку , :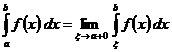 
.
В случае, если функция интегрируема по Риману (по Лебегу) на каждом отрезке , и существуют несобственные интегралы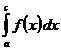 
и 
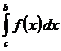, то существует несобственный интеграл 
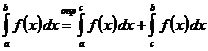и он не зависит от выбора точки .
К примеру,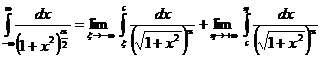 
сходится при любых и расходится при .
В случае, если на промежутке имеется конечное число точек , , таких, что функция интегрируема по Риману (по Лебегу) на каждом отрезке , не содержащем ни одной точки , и для каждого , существует несобственный интеграл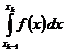 
, то несобственный интеграл 
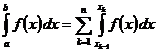. Это определение не зависит от выбора точек .
На несобственные интегралы переносятся неспециализированные особенности интегралов: линейность, аддитивность относительно промежутков, по которым производится интегрирование, правило интегрирования неравенств, теоремы о среднем, интегрирование по частям и замены переменного, формула Ньютона-Лейбница. К примеру, в случае, если функция практически везде на сходится с производной функции , которая полностью постоянна на каждом отрезке , ,то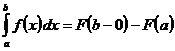 
. Конкретный пример: 
.
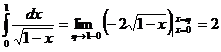Для выяснения сходимости несобственного интеграла от знакопостоянных функций используется показатель сравнения. К примеру, как мы знаем, что при , , , , тогда из сходимости несобственного интеграла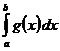 
направляться сходимость несобственного интеграла 
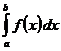. Функция именуется в этом случае функцией сравнения. В качестве функции сравнения довольно часто употребляется степенная функция, что показано в приведённых примерах.
Нужное и достаточное условие сходимости несобственного интеграла даёт критерий Коши. Так, несобственный интеграл на сходится тогда и лишь тогда, в то время, когда для любого существует такое , что для всех , выполняется неравенство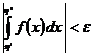 
.
Несобственный интеграл 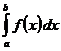именуется полностью сходящимся, в случае, если сходится несобственный интеграл 
.
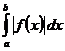В случае, если несобственный интеграл полностью сходится, то он сходится и сходится с интегралом Лебега. Существуют несобственные интегралы сходящиеся, но не полностью сходящиеся. К примеру, для конечного промежутка несобственный интеграл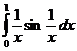 
, а для нескончаемого 
.
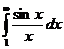Существуют разные показатели сходимости несобственного интеграла. К примеру, в случае, если на полуоси функция имеет ограниченную первообразную, а – монотонная функция, стремящаяся к нулю при , то интеграл сходится. Второй показатель: в случае, если несобственный интеграл сходится, а функция монотонна и ограничена при , то несобственный интеграл сходится.
Сходимость несобственного интеграла возможно выразить в терминах сходящихся последовательностей. К примеру, чтобы несобственный интеграл по сходился, нужно и достаточно, дабы для любой последовательности , сходился последовательность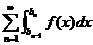 
, причем при сходимости последовательности его сумма сходится с несобственным интегралом.
Понятие несобственного интеграла обобщается для функций многих переменных.
Определение. Функция , определенная на открытом (ограниченном либо неограниченном) множестве именуется интегрируемой в несобственном смысле по множеству , в случае, если для любой последовательности измеримых по Жордану множеств таких, что ,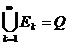 
, существует 
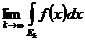, не зависящий от выбора указанной последовательности. Данный предел, если он существует, именуется несобственным интегралом 
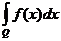. При он существует тогда и лишь тогда, в то время, когда существует несобственный интеграл 
.
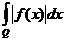Итак, в отличие от одномерного случая в многомерной области функция интегрируема в несобственном смысле тогда и лишь тогда, в то время, когда она полностью несобственно интегрируема. Другими словами в многомерном случае интеграл Римана, осознаваемый в определенном смысле либо несобственном смысле, есть интегралом Лебега.
В приложениях довольно часто появляются повторные интегралы. Связь между повторными интегралами и кратными Лебега устанавливает
Теорема Фубини. Пускай ограниченная n-мерная область переменных , а ограниченная m-мерная область переменных , в ограниченной области (n+m)-мерного пространства переменных (x,y) задана функция f(x,y). В случае, если функцияf(x,y) интегрируема по , то f(x,y) для практически всех интегрируема по , для практически всех f(x,y) интегрируема по , функци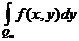и 
и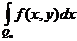 
интегрируемы по и по соответственно и
.
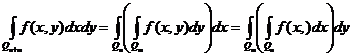Напомним, что из существования повторных интегралов, по большому счету говоря, не нужно их существование и равенство двойного интеграла. На практике в большинстве случаев пользуются следствием теоремы Фубини: в случае, если функция f(x,y) неотрицательна, то из существования хотя бы одного повторного интеграла направляться существование двойного: , а тогда честна теорема Фубини, другими словами существует второй повторный интеграл и выполнено равенство всех трех интегралов.
К несобственным интегралам относятся интегралы в смысле главного значения.
Определение. Пускай функция выяснена на открытом множестве не считая, возможно, точки , и пускай для любого функция интегрируема по Риману либо по Лебегу на множестве где — шар радиуса с центром . Тогда, в случае, если существует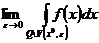 
, то его именуют интегралом в смысле главного значения и обозначают 
.
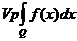В случае, если существует несобственный интеграл 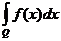, то он существует и в смысле главного значения. Обратное, по большому счету говоря, неверно. К примеру, несобственный интеграл расходится, а 
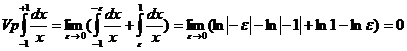. Подобно определяется интеграл в смысле главного значения в бесконечности: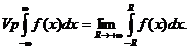 
Общность, достигнутая определением интеграла в смысле Лебега, очень значительна во многих вопросах современного матанализа: теория обобщенных функций, определение обобщенных ответов дифференциальных уравнений, изоморфизм гильбертовых пространств и . Все эти теории были вероятными лишь при понимании интеграла в смысле Лебега.
Первообразную в смысле Лебега определяют равенством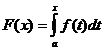 
, в котором интеграл понимается в смысле Лебега. При таком понимании равенство будет справедливо практически везде. В частности, это равенство выполнено во всех точках непрерывности функции .
Понятие неизвестного, определенного интеграла и интегралов в смысле главного значения переносятся на случай функций комплексного переменного.