a (А, L) – плоскость a выяснена точкой А и прямой L;
Ф (S, m) – коническая поверхность Ф выяснена вершиной S и
направляющей – m.
II. Главные геометрические отношения между
Геометрическими элементами
1. ?? – параллельность;
L?? m – прямая L параллельна прямой m;
2. ^ – перпендикуляр;
m ^ Т – прямая m перпендикулярна плоскости Т;
3. – скрещивание;
m Т – скрещивающиеся прямые m и L;
4. I – принадлежность для элемента;
I – для подмножества;
А I L – точка А лежит на прямой L;
h I a – прямая h в собственности плоскости a;
5. C – пересечение;
L C Т – прямая L пересекает плоскость Т;
6. E – соединение, объединение;
m=AEB – прямая m получается в следствии соединения точек А и В;
1IIE2II=mII – соединение проекции точек 1II и 2II (дает проекцию прямой mII);
7. = – итог построения;
8. º – совпадение, АIIºВII;
9. ? – в случае, если … то;
ZA=0?AIПI – в случае, если координата Z точки А равна 0, то точка А лежит
на плоскости ПI;
10. cА, В c – протяженность отрезка; расстояние от точки А до точки В;
cА, L c – расстояние от точки А до прямой L;
11. ? – угол ?a, ?b…;
12. U – величина угла;
LUПI – угол образованный прямой L с плоскостью ПI;
13. cLUПi – натуральная величина угла.
Тема 1, 2. Точка, прямая, плоскость
Контрольные вопросы
1. Как именуются плоскости проекций ПI, ПII, ПIII? Как дробят они пространство?
Что такое оси проекций?
3. Что именуется центральной, параллельной и ортогональной проекцией точки? Что именуется эпюром?
4. Что именуется координатами точки? Какими координатами точки определяется положение на эпюре ее горизонтальной, фронтальной и профильной проекций?
5. Перечислить характерные показатели размещения проекций точки относительно оси Х, в случае, если точку перемещать в различные углы пространства?
6. В чем содержится способ Монжа?
7. Какая прямая именуется прямой неспециализированного положения?
8. Какая прямая именуется горизонтальной, фронтальной, профильной?
9. Какие конкретно прямые именуются проецирующими прямыми?
10. Показатель принадлежности точки прямой линии на эпюре.
11. Что именуется следом прямой линии?
12. Чему равна координата Y для фронтального следа прямой и координата Z для горизонтального следа прямой?
13. Чему равна натуральная величина отрезка прямой неспециализированного положения?
14. Как определяют углы наклона прямой к плоскости проекции ПI и ПII?
15. Что есть показателем параллельных прямых на эпюре?
16. Что есть показателем пересекающихся прямых на эпюре?
17. Как выяснить на эпюре видимость соперничающих точек, которыми владел скрещивающимся прямым?
18. В каком случае прямой угол проецируется в натуральную величину?
19. Какими геометрическими элементами возможно задана плоскость?
20. Перечислить типовые случаи размещения плоскости относительно плоскостей проекций.
21. В каком случае прямая в собственности плоскости?
22. В каком случае точка лежит в плоскости?
23. Перечислить проецирующие плоскости. Какими особенностями они владеют?
24. Какие конкретно плоскости именуются плоскостями уровня? Перечислить их.
25. Какие конкретно линии плоскости именуются главными?
26. Какая из основных линий помогает для определения угла наклона плоскости к плоскостям проекции?
| Тема 1, 2 | Проекционные базы чертежа | Упражнения | ||||
| 1 | Назвать элементы чертежа | |||||
| Х12 — ___________________________________________________________ АI — ___________________________________________________________ АII — ___________________________________________________________ АIАII — ___________________________________________________________ AIAX — ___________________________________________________________ AIIAX — ___________________________________________________________ | ||||||
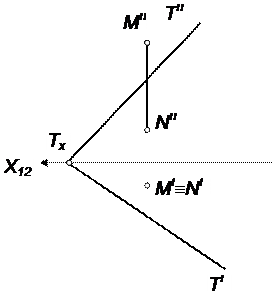
| 2 | По наглядному изображению выстроить эпюры точек А и В и записать их координаты | |||||
| A (_______________) B (_______________) | ||||||
| Тема 1, 2 | Проекционные базы чертежа. Точка | Упражнения | ||||
| 3 | Выстроить по координатам изображение точек и выяснить их положение в пространстве | |||||
| А (35, 10, 40) В (10, 30, -20) С (25, -20, -15) D (50, 0, 25) Е (65, -30, 0) F (80, 0, 0) N (90, 30, 30) | ||||||
| 4 | Выстроить недостающие проекции точек и выяснить их координаты | |||||
| Тема 1, 2 | Прямая | Упражнения | ||||
| 5 | Выстроить эпюр отрезка АВ и записать координаты финишей отрезка | |||||
| 6 | Достроить недостающие проекции точек А и В, в случае, если точка А в собственности прямой m, а точка В расположена выше прямой m. Выстроить на прямой m точку С, равноудаленную от плоскостей проекции ПI и ПII | |||||
| Тема 1, 2 | Прямая | Упражнения | ||||
| 7 | Выстроить через точку А горизонтальную прямую h под углом 45° к плоскости ПII, а через точку В фронтальную прямую под углом 30° к плоскости ПI. Выстроить их следы | |||||
| 8 | Выстроить следы прямой m и указать на эпюре, через какие конкретно четверти пространства она проходит | |||||
| Тема 1, 2 | Прямая | Упражнения | ||||
| 9 | Выяснить натуральную величину углы наклона и отрезка АВ его к плоскостям ПI и ПII | |||||
| 10 | Выстроить проекции отрезка АВ по заданным координатам его финишей: А (30, 10, 10), В (90, 25, 40). Выстроить проекции точки С, дробящей отрезок в отношении АС/СВ=2/3 | |||||
| Тема 1, 2 | Прямая | Задачи | ||||
| 11 | Отыскать недостающие проекции точек С и D, которыми владел отрезку АВ, не строя профильную проекцию отрезка | |||||
| 12 | Достроить фронтальную проекцию отрезка АВ, расположенного под углом 30° к плоскости ПI. Выяснить на отрезке АВ точку С, отстоящую от точки А на 40см | |||||
| Тема 1, 2 | Относительное положение прямых | Задачи | ||||
| 13 | Выяснить расстояние от точки К до прямой h | |||||
| 14 | Через точку М совершить прямую, пересекающую отрезки АВ и СД | |||||
| Тема 1, 2 | Относительное положение прямых | Задачи | ||||
| 15 | Выстроить проекции фронтальной прямой f, пересекающейся с отрезками прямых АВ и СД и расположенной под углом 30° к плоскости ПI | |||||
| а) б) | ||||||
| 16 | Через точку А совершить прямую, которая пересекла бы заданную прямую ВС в точке К, удаленной от плоскости ПI на 10мм. Решить двумя методами | |||||
| Тема 1, 2 | Плоскость | Упражнения | ||||
| 17 | Как именуется любая из данных плоскостей? Написать наименование | |||||
| 1 ______________ 2_______________ 3______________ 4 _____________ ______________ _______________ ______________ _____________ | ||||||
| 18 | Через прямую неспециализированного положения совершить: а) фронтально-проецирующую плоскость a; б) горизонтально-проецирующую плоскость Т; в) плоскость неспециализированного положения | |||||
| а) б) в) | ||||||
| Тема 1, 2 | Плоскость | Упражнения | ||||
| 19 | Выстроить нехватающую проекцию прямой, лежащей в плоскости | |||||
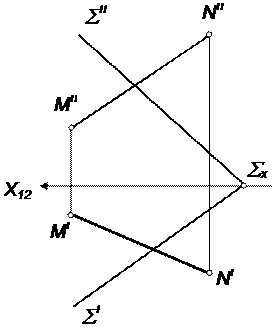
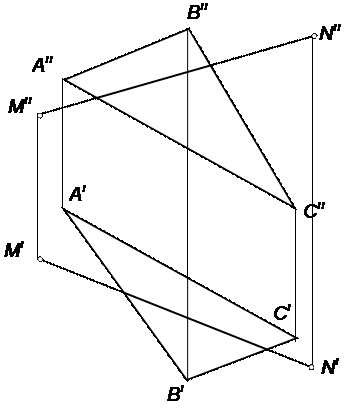
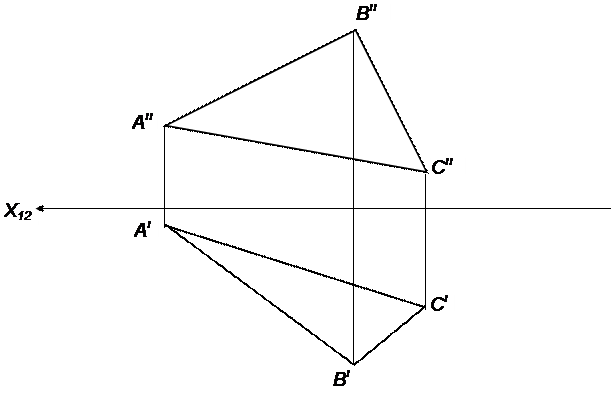
| 20 | Выстроить точку М в плоскости АВС, в случае, если ее расстояние до плоскости ПI равняется 30мм, и точку N, отстоящую от плоскости ПII на 20мм | |||||
|
||||||
| Тема 1, 2 | Плоскость | Упражнения | ||
| 21 | Через точку А провести в плоскости АВС горизонталь, а через точку С – фронталь | |||
| а) б) | ||||
| Тема 1, 2 | Плоскость | Задачи | ||
| 22 | Отыскать нехватающую проекцию точки К, принадлежащей плоскости Т (А, L) | |||
| 23 | Выяснить углы наклона a и b плоскости АВС к плоскостям проекций ПI и ПII | |||
| Тема 1, 2 | Плоскость | Задачи | ||
| 24 | Выстроить в заданных плоскостях горизонталь на расстоянии 20мм от плоскости ПI и фронталь на расстоянии 25мм от плоскости ПII Т | |||
| 25 | Выстроить горизонтальную проекцию треугольника АВС. Сторона АВ лежит в плоскости ПII. Угол наклона плоскости АВС к плоскости ПII равен 30° | |||
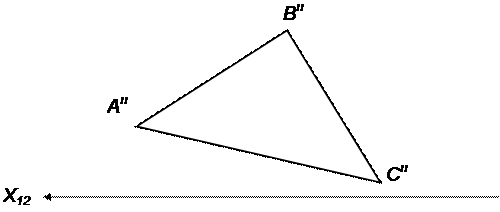
|
||||
Тема 3. Позиционные задачи. Обоюдное положение прямой и
плоскости, двух плоскостей
Контрольные вопросы
1. В каком случае прямая параллельна плоскости? Метод ее решения.
2. Как через прямую линию совершить плоскость, параллельную заданной прямой?
3. Как выяснить обоюдную параллельность двух плоскостей?
4. Условие параллельности двух профильно-проецирующих плоскостей.
5. Как отыскать точку встречи прямой с проецирующей плоскостью?
6. Как отыскать линию пересечения двух плоскостей:
а) в случае, если одна из плоскостей проецирующая;
б) обе плоскости неспециализированного положения.
7. Как отыскать точку встречи прямой с плоскостью неспециализированного положения?
8. Как выяснить «видимость» прямой линии при пересечении ее с плоскостью?
Литература: [1 гл.IV]
Тема 4. Прямая, перпендикулярная плоскости.
Две взаимно перпендикулярные плоскости
Контрольные вопросы
1. В то время, когда прямая перпендикулярна плоскости?
2. Как совершить плоскость, перпендикулярную заданной прямой:
а) через точку на прямой?
б) через точку вне прямой?
3. В каких случаях обоюдная перпендикулярность одной пары одноименных следов плоскостей соответствует обоюдной перпендикулярности самих плоскостей??
4. Как выстроить взаимно перпендикулярные плоскости?
5. Как совершить перпендикуляр из точки на прямую неспециализированного положения?
6. Перпендикулярны ли плоскости неспециализированного положения, в случае, если их одноименные следы перпендикулярны?
Литература: [1 §28, 29, 30]
| Тема 4 | Позиционные задачи. Прямая, перпендикулярная плоскости | Упражнения | |||
| 35 | Через точку А совершить прямую, перпендикулярную заданной плоскости | ||||
| а) б) в) г) | |||||
| Тема 4 | Две перпендикулярные плоскости | Упражнения | |||
| 36 | Через прямую MN совершить плоскость, перпендикулярную заданной | ||||
| а) б) | |||||
| 37 | Задать следами плоскость, проходящую через точку А и перпендикулярную заданной прямой | ||||
| а) б) в) | |||||
| Тема 4 | Перпендикулярность плоскостей и прямых | Задачи | |||
| 38 | Отыскать проекции перпендикуляра, опущенного из точки А на заданную плоскость | ||||
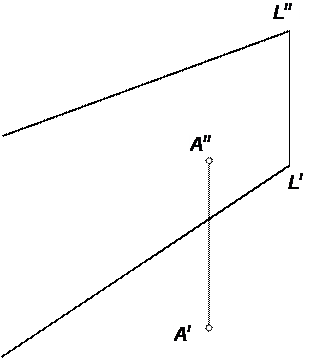
| 39 | Отыскать основание перпендикуляра, опущенного из точки А на прямую L | ||||
|
|||||
Тема 5. Методы преобразования чертежа
Контрольные вопросы
1. С какой целью производится преобразование чертежа?
2. В чем содержится метод замены плоскостей проекций?
3. Какое положение довольно заданной совокупности плоскостей проекций занимает снова вводимая совокупность плоскостей проекций?
4. На каком расстоянии от новой оси проекций находится новая проекция точки и по какой причине?
5. какое количество новых плоскостей проекций нужно ввести, дабы в новой совокупность плоскостей проекций:
а) прямая уровня заняла проецирующее положение;
б) прямая неспециализированного положения заняла проецирующее положение;
в) проецирующая плоскость заняла положение плоскости уровня;
г) плоскость неспециализированного положения заняла положение плоскости уровня?
6. В какой последовательности методом замены плоскостей проекций:
а) чертеж прямой неспециализированного положения преобразуется в чертеже проецирующей прямой;
б) чертеж плоскости неспециализированного положения преобразуется в чертеж плоскости уровня?
7. В чем состоит сущность метода вращения около прямой линии? В чем его главное отличие от метода замены плоскостей проекций?
8. Какие конкретно задачи решаются методом вращения около проецирующих прямых?
9. В чем содержится метод вращения около основных линий и какие конкретно задачи решаются этим методом?
10. В чем содержится метод плоско-параллельного перемещения и какие конкретно задачи решаются этим методом?
11. Каковы особенности метода совмещения? Для решения каких задач он используется?
Литература: [1 гл.V]
| Тема 5 | Метод замены плоскостей проекций | Упражнения | |||
| 40 | Выяснить расстояние между двумя скрещивающимися отрезками прямых АВ и СD | ||||
| 41 | Выяснить величину двугранного угла при стороне ВС | ||||
| Тема 5 | Метод замены плоскостей проекций | Задачи | |||
| 42 | Выстроить нехватающую проекцию АII точки А, удаленной от плоскости a на 20мм | ||||
| 43 | Выяснить натуральную величину его угол и отрезка АВ наклона к фронтальной плоскости проекций | ||||
| Тема 5 | Способ плоско-параллельного перемещения. Вращение около основных линий плоскости | Упражнения | |||
| 44 | Выяснить натуральную величину треугольника АВС | ||||
| 45 | Выяснить натуральную величину угла между прямыми а и b при вершине С | ||||
| Тема 5 | Вращение около: а) проецирующих прямых; б) основных линий плоскости | Задачи | |||
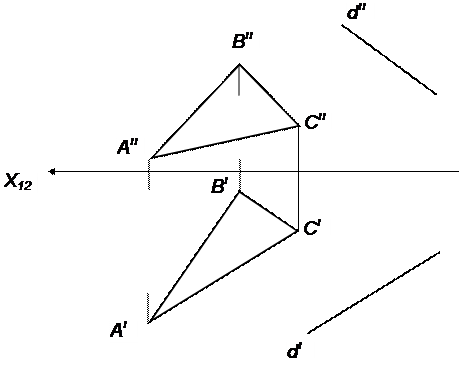
| 35 | Выяснить угол наклона d к плоскости треугольника АВС | ||||
|
|||||
Тема 6. Многогранники
Контрольные вопросы
1. Как именно многогранники изображаются на комплексном чертеже?
2. Какие конкретно многогранники именуются верными? Назвать узнаваемые многогранники.
3. Как выяснить видимость точки, лежащей на поверхности многогранника?
4. Как выяснить недостающие проекции точки, лежащей на поверхности многогранника?
5. К чему сводится построение сечения многогранника плоскостью?
6. Что нужно учитывать, в случае, если плоскость либо грани многогранника проецирующие:
7. Что нужно для определения поверхности многогранника и взаимного положения прямой?
8. Что направляться применять, в случае, если прямая либо грани многогранника являются проецирующими?
9. Поведать о нахождении линии пересечения двух многогранников?
Литература: [1, гл. V]
Тема 7. Кривые линии
Контрольные вопросы
1. Какие конкретно линии именуются плоскими кривыми линиями?
2. Указать методы задания плоских кривых линий.
3. Дать определение кривых второго порядка: эллипса, преувеличения, параболы.
4. Что такое кривизна плоской кривой линии?
5. Чему равна кривизна окружности?
6. Образование цилиндрической винтовой линии. Определение единичного шага и шага винтовой линии.
Литература: [1, гл.VII]
| Тема 6 | Многогранники | Упражнения | |||
| 47 | Выстроить две проекции наклонной призмы по заданному основанию АВС и ребру АD. Невидимые ребра нанесите штриховыми линиями | ||||
| 48 | Выяснить недостающие проекции точек, которыми владел поверхности многогранника. Указать видимость | ||||
| Тема 6 | Многогранники | Упражнение Задачи | |||
| 49 | Выстроить проекции сечения пирамиды | ||||
| а) проецирующей плоскостью б) плоскостью неспециализированного положения | |||||
| Тема 6 | Многогранники | Упражнение | |||
| 50 | Отыскать точку встречи прямой а с поверхностью многогранника. Выяснить видимость | ||||
| Тема 6 | Многогранники | Задача | |||
| 51 | Выстроить линию пересечения двух многогранников | ||||
| Тема 7 | Плоские кривые линии | Упражнения | |||
| 52 | Выстроить эллипс по громадной оси АВ=80мм и малой оси CD=40мм | ||||
| Тема 7 | Пространственные кривые линии | Упражнения | |||
| 53 | Выстроить недостающие проекции точек. Указать величину углового и осевого смещения точки А относительно точки В | ||||
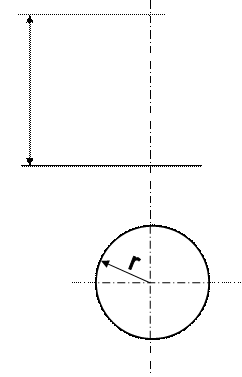
| 54 | Выстроить винтовую линию левого хода по заданному шагу Н и радиусу r | ||||
|
|||||
Тема 8-11. Кинематические поверхности главных видов.
Пересечение поверхности плоскостью неспециализированного положения
Контрольные вопросы
1. Дайте определение кинематической поверхности.
2. Назовите главные методы задания поверхности и изложите их сущность.
3. Что именуется каркасом, очерком и сетью поверхности?
4. Какие конкретно поверхности именуются линейчатыми?
5. Как образуются поверхности вращения, какие конкретно линии на этих поверхностях именуются параллельными, меридианами, что такое экватор и главный меридиан?
6. Что именуется сечением поверхности?
7. Как именуются кривые линии пересечения цилиндра, конуса, шара проецирующей плоскостью?
8. В чем содержится метод нахождения точек пересечения прямой линии с поверхностью? Привести схему ответа задачи.
9. Какие конкретно сечения кривых поверхностей именуются несложными?
10. Какие конкретно точки сечения именуются опорными?
11. Как выяснить «высшую» и «низшую» точки сечения? (Либо громадную ось эллипса).
12. Как определяются точки, служащие границей видимой и невидимой части сечения?
13. Как определяют проекции малой оси эллипса?
14. Какой способ положен в базу построения фигуры сечения поверхности плоскостью?
Литература: [1, гл. VIII-IX]
| Тема 8-11 | Поверхность | Задачи | ||
| 55 | Выстроить недостающие проекции точек, которыми владел поверхности | |||
| Тема 8-11 | Поверхность | Упражнение | ||
| 56 | Назвать линии, полученные в сечении конуса различно расположенными проецирующими плоскостями | |||
| Тема 8-11 | Поверхность | Упражнение | ||
| 57 | Выстроить проекции сечения и третью проекцию цилиндра его плоскостью S | |||
| Тема 8-11 | Поверхность | Задачи | ||
| 58 | Выстроить точки встречи прямой с поверхностью конуса, тора и шара | |||
| а) б) в) | ||||
| Тема 8-11 | Пересечение поверхности плоскостью неспециализированного положения | Задача | ||
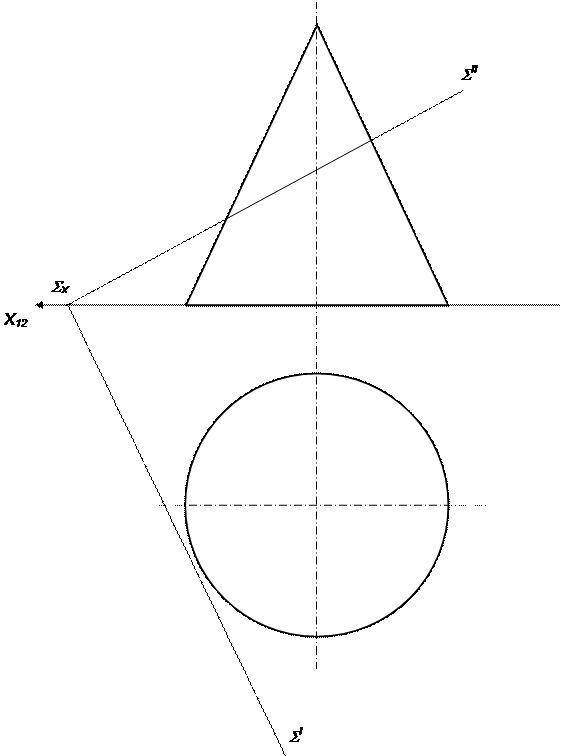
| 59 | Выстроить сечение конуса плоскостью неспециализированного положения S | |||
|
||||
Тема 12. Обоюдное пересечение поверхностей
Контрольные вопросы
1. Как возможно отыскать линию пересечения двух поверхностей?
2. В то время, когда линией пересечения будет:
а) пространственная кривая;
б) пространственная ломаная кривая;
в) плоская линия (прямая, окружность, эллипс и т.д.);
3. В чем содержится и в то время, когда используется способ запасных секущих плоскостей?
4. В чем содержится и в то время, когда используется способ сфер?
Литература: [1, гл.X]
Тема 13. Развертывание гранных и кривых поверхностей
Контрольные вопросы
1. Дать определение развертки поверхности геометрического тела.
2. Поверхности развертывающиеся и неразвертывающиеся.
3. Указать, по каким схемам возможно создавать пирамиды и развёртывание поверхностей.
4. Указать примеры построения разверток:
а) цилиндрических поверхностей;
б) конических поверхностей;
5. Как выстроить развертку боковой поверхности