Дана автокорреляционная функция временного последовательности
Верным будет утверждение, что последовательность …имеет выраженную сезонную компоненту с лагом 4
3. Автокорреляционной функцией временного последовательности именуется последовательность коэффициентов автокорреляции …
первого, второго, третьего и последующих порядков
4. Значение коэффициента автокорреляции второго порядка равняется (-0,6), следовательно, последовательность содержит …тенденцию
5. Автокорреляцией уровней последовательности именуется корреляционная зависимость между …последовательными уровнями последовательности
1. Уровень временного последовательности (yt) формируется под действием разных факторов – компонент: Т (тенденция), S (циклические и/либо сезонные колебания), Е (случайные факторы). Для аддитивной модели временного последовательности для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного последовательности y3 будет равняется …10,65
2. Уровень временного последовательности (yt) формируется под действием разных факторов – компонент: Т (тенденция), S (циклические и/либо сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного последовательности, содержащего периодические колебания в 4 момента, взяты значения сезонных компонент: S1 = 2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256. Известны значения компонент: T5 = 20,6 и E5 = 0,4. Вычислите значение уровня временного последовательности y5.17,2
3. Для аддитивной модели временного последовательности Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент: , , . равна …1
4. Для мультипликативной модели временного последовательности Y = T · S · E сумма скорректированных сезонных компонент равна …лагу
1. Как мы знаем, что дисперсия временного последовательности Y возрастает с течением времени. Значит, последовательность Y …нестационарным
2. Как мы знаем, что временной последовательность Y порожден случайным процессом, что по своим чертям есть «белым шумом». Значит, последовательность Y …стационарный
3. Как мы знаем, что временной последовательность Y характеризуется устойчивой тенденцией, другими словами его среднее значение изменяется. Значит, последовательность Y, вероятнее,есть …нестационарным
4. Для временного последовательности известны характеристики: – дисперсия и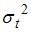 
– среднее. В случае, если временной последовательность есть стационарным, то …
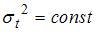
1. Левая часть совокупности эконометрических уравнений представлена совокупностью _________ переменных.зависимых
2. предложения равенства и Модель спроса, где спрос и предложение являются линейными функциями цены p, складывается из уравнений …
3. Совокупностью эконометрических уравнений не есть совокупность линейных _____ уравнений.
обычных
стандартизованных
2. Изучаются модели предложения и зависимости спроса от цены p и других факторов. Установите соответствие между классом и видом эконометрических уравнений.
свободные(1)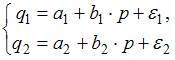 
одноврем(2)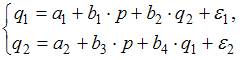 
рекурс(3)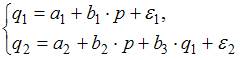 
совокупность свободных уравнений
совокупность одновременных уравнений
совокупность рекурсивных уравнений
Установите соответствие между классом и видом эконометрических уравнений.
незав(1)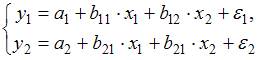 
рекурс(2)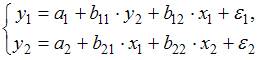 
одноврем(3)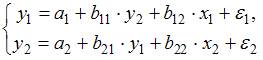 
совокупность свободных уравнений
совокупность рекурсивных уравнений
совокупность одновременных уравнений
4. Установите соответствие между классом системы и видом эконометрических уравнений:
(1) 
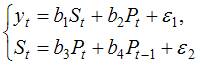
(2) 
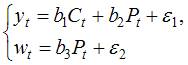
совокупность одновременных уравнений с лаговыми переменными
совокупность свободных уравнений
2. Дана структурная форма модели совокупности одновременных уравнений:
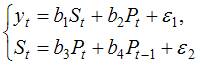
Установите соответствие между его наименованием и обозначением:
(1) -неточность модели
(2) -лаговая
(3) -эндоген
Совокупность свободных эконометрических уравнений возможно идентифицирована посредством простого способа мельчайших квадратов. Выясните последовательность этапов метода оценки параметров для таковой модели.
1.оценка возможности идентификации модели как совокупности свободных уравнений
2.построение неспециализированного вида совокупности обычных уравнений для каждого уравнения совокупности и расчет нужных значений сумм
3.ответ совокупности обычных уравнений для каждого уравнения совокупности
4.подстановка отысканных значений оценок параметров в уравнения совокупности
3. Дана совокупность одновременных эконометрических уравнений:
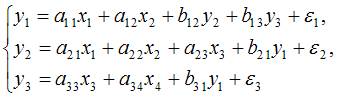
Совокупность есть совершенно верно идентифицируемой. Выясните последовательность этапов метода оценки ее параметров.
1.преобразование структурной формы модели в приведенную форму вида
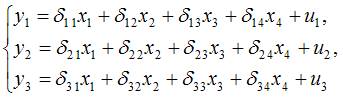
2.оценивание параметров приведенной формы модели (приведенных коэффициентов) для каждого уравнения приведенной формы модели простым МНК оцениваются
3.изменение коэффициентов приведенной формы модели в параметры структурной формы модели и
4.подстановка отысканных значений коэффициентов в структурную форму совокупности эконометрических уравнений
5. При проверке счетного правила стало известно, что для всех уравнений совокупности одновременных уравнений выполняется нужное условие идентификации и все уравнения по счетному правилу совершенно верно идентифицируемы. Чтобы получить структурные коэффициенты совокупности, действия необходимо выполнить в такой последовательности:
1.для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
2.преобразовать структурную форму модели в приведенную форму модели
3.для каждого уравнения приведенной формы модели простым способом мельчайших квадратов оценить приведенные коэффициенты
4.коэффициенты приведенной формы модели преобразовать в параметры структурной модели
6. При проверке счетного правила стало известно, что для всех уравнений совокупности одновременных уравнений выполняется нужное условие идентификации и все уравнения по счетному правилу сверхидентифицируемы. Чтобы получить структурные коэффициенты совокупности, действия необходимо выполнить в такой последовательности:
1.для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
2.преобразовать структурную форму модели в приведенную форму модели
3.для каждого уравнения приведенной формы модели простым способом мельчайших квадратов оценить приведенные коэффициенты
4.на базе коэффициентов приведенной формы модели взять теоретические значения эндогенных переменных, содержащихся в правой части сверхидентифицированных уравнений
5 применить простой способ мельчайших квадратов, подставив вместо фактических значений эндогенных переменных, стоящих в правой части уравнения, вычисленные теоретические значения, и взять структурные коэффициенты модели
1. По 72 банкам выстроено уравнение зависимости размеров кредитов, выданных организациям и предприятиям, в млн. руб. (y) от собственного капитала, миллионов рублей. (x): y = 710,967 + 3,057 • x . Данные упорядочены по убыванию величины собственного капитала. По размерам остатков вычислен коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.
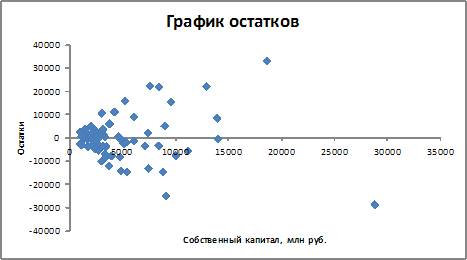
Проанализировав график остатков, возможно сделать вывод о том, что …
нарушена предпосылка о гомоскедастичности остатков
Дана матрица парных коэффициентов корреляции.
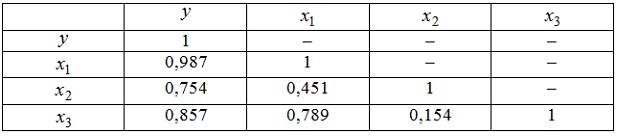Коллинеарными являются факторы …
и коллинеарны.
4. В модели множественной регрессии определитель матрицы парных коэффициентов корреляции между факторами , и близок к нулю. Это указывает, что факторы , и …мультиколлинеарность факторов.
5. Для эконометрической модели линейного уравнения множественной регрессии вида выстроена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4)– свободные переменные):
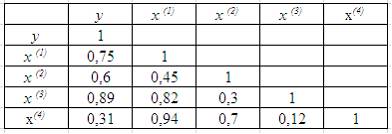
Коллинеарными (тесно связанными) свободными (растолковывающими) переменными не являются …x(2) и x(3)
1. Дана таблица данных для построения эконометрической регрессионной модели:
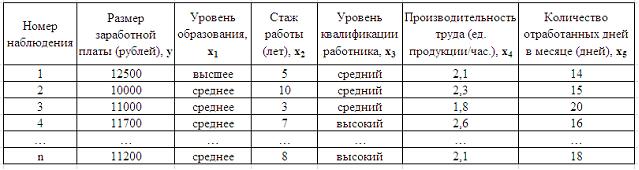Фиктивными переменными не являются …
стаж работы
производительность труда
2. При изучении зависимости потребления мяса от уровня дохода и пола потребителя возможно советовать …
применять фиктивную переменную – пол потребителя
поделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
3. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие разглядываемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии: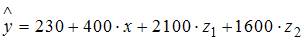 
,
где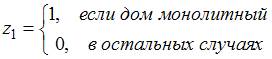 
, 
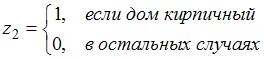
Частными уравнениями регрессии для кирпичного и монолитного являются …
для типа дома кирпичный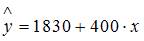 
для типа дома монолитный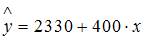 
4. При анализе предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были выстроены три частных уравнения регрессии:
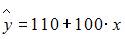для Республики Марий Эл;
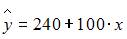для Республики Чувашия;
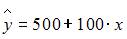для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.
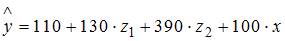
5. В эконометрике фиктивной переменной принято вычислять …
переменную, принимающую значения 0 и 1
обрисовывающую количественным образом качественный показатель
1. Для регрессионной модели зависимости среднедушевого финансового дохода населения (руб., у) от количества валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение . Величина коэффициента регрессии при переменной х2 говорит о том, что при трансформации уровня безработицы на 1% среднедушевой финансовый доход ______ рубля при неизменной величине валового регионального продукта.
изменится на (-1,67)
2. В уравнении линейной множественной регрессии: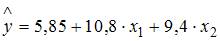 
, где – цена главных фондов (тыс. руб.); – численность занятых (тыс. чел.); y – количество производства (тыс. руб.) параметр при переменной х1, равный 10,8, свидетельствует, что при повышении количества главных фондов на _____ количество производства _____ при постоянной численности занятых.
на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
3. Как мы знаем, что часть остаточной дисперсии зависимой переменной в ее неспециализированной дисперсии равна 0,2. Тогда значение коэффициента детерминации образовывает …0,8
4. Выстроена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): . Следовательно, средний размер прибыли от реализации, не зависящий от количества оборотных средств предприятия, образовывает _____ рубля. 10,75
5. F-статистика рассчитывается как отношение ______ дисперсии к ________ дисперсии, рассчитанных на одну степень свободы.факторной … остаточной
1. Для эконометрической модели уравнения регрессии неточность модели определяется как ______ между фактическим значением зависимой переменной и ее расчетным значением.Разность
2. Величина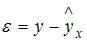 
именуется …случайной составляющей
3. В эконометрической модели уравнения регрессии величина отклонения фактического значения зависимой переменной от ее расчетного значения характеризует …неточность модели
4. Как мы знаем, что часть растолкованной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации образовывает … 0,2
5. При способе мельчайших квадратов параметры уравнения парной линейной регрессии определяются из условия ______ остатков .минимизации суммы квадратов
1. Для обнаружения автокорреляции в остатках употребляется …
статистика Дарбина – Уотсона
2. Как мы знаем, что коэффициент автокорреляции остатков первого порядка равен –0,3. Кроме этого даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при малоизвестном и количестве наблюдений , . Согласно данным чертям возможно сделать вывод о том, что …автокорреляция остатков отсутствует
3. Значение критерия Дарбина – Уотсона возможно примерно вычислить по формуле , где – значение коэффициента автокорреляции остатков модели. Минимальная величина значения будет наблюдаться при ________ автокорреляции остатков. хорошей
4. Из перечисленного условием исполнения предпосылок способа мельчайших квадратов не есть ____ остатков.гетероскедатичность
5. Значение критерия Дарбина – Уотсона возможно примерно вычислить по формуле , где – значение коэффициента автокорреляции остатков модели. Большая величина значения будет наблюдаться при ________ автокорреляции остатков.отрицательной
1. Пускай – оценка параметра регрессионной модели, полученная посредством способа мельчайших квадратов;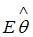 
– математическое ожидание оценки . В том случае в случае, если 
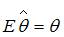, то оценка владеет свойством …несмещенности
2. Из несмещенности оценки параметра направляться, что среднее значение остатков равняется …0
3. Несмещенность оценок параметров регрессии свидетельствует, что …
математическое ожидание остатков равняется нулю
4. В случае, если оценка параметра есть смещенной, то нарушается предпосылка способа мельчайших квадратов о _________ остатков.
нулевой средней величине
5. Состоятельность оценок параметров регрессии свидетельствует, что …
точность оценок выборки возрастает с повышением количества выборки
1. При нарушений предпосылок способа мельчайших квадратов используют обобщенный способ мельчайших квадратов, что употребляется для оценки параметров линейных регрессионных моделей с __________ остатками. автокоррелированными и/либо гетероскедастичными
2. При наличии гомоскедастичности автокорреляции и нарушении остатков остатков рекомендуется использовать _____________ способ мельчайших квадратов.Обобщенный
3. Пускай y – издержки производства, – количество продукции, – главные производственные фонды, – численность работников. Как мы знаем, что в уравнении дисперсии остатков пропорциональны квадрату численности работников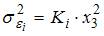 
.
По окончании применения обобщенного способа мельчайших квадратов новая модель приняла вид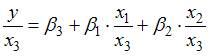 
. Тогда параметр в новом уравнении характеризует среднее изменение затрат …
на работника при повышении производительности труда на единицу при неизменном уровне фондовооруженности труда
4. Обобщенный способ мельчайших квадратов не имеет возможности использоваться для оценки параметров линейных регрессионных моделей , если …средняя величина остатков не равна нулю
5. Пускай y – издержки производства, – количество продукции, – главные производственные фонды, – численность работников. Как мы знаем, что в уравнении дисперсии остатков пропорциональны квадрату количества продукции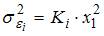 
.
Применим обобщенный способ мельчайших квадратов, поделив обе части уравнения на По окончании применения обобщенного способа мельчайших квадратов новая модель приняла вид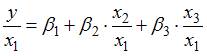 
. Тогда параметр в новом уравнении характеризует среднее изменение затрат на единицу продукции при повышении …
фондоемкости продукции при неизменном уровне трудоемкости продукции
1. Для эконометрической модели вида показателем тесноты связи между переменными и есть парный коэффициент линейной …корреляции
2. Самым маленьким промежутком трансформации коэффициента корреляции для уравнения парной линейной регрессии есть …[–1; 0]
3. Самым маленьким промежутком трансформации показателя множественной корреляции для уравнения множественной линейной регрессии , в случае, если известны парные коэффициенты корреляции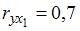 
, 
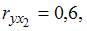есть промежуток …[0,7; 1]
4. Для регрессионной модели вида взята диаграмма
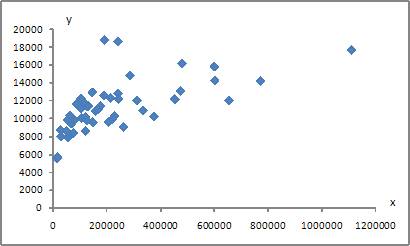
Такое графическое отображение именуется …полем корреляции
1. Как мы знаем, что часть остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равняется …0,9
2. Как мы знаем, что общая сумма квадратов отклонений 
, а остаточная сумма квадратов отклонений,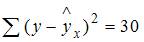 
. Тогда значение коэффициента детерминации равняется …0,8
3. Для регрессионной модели вида , где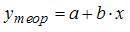 
вычислены дисперсии: 
; 
; 
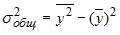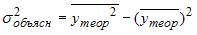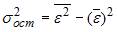. Тогда величина 
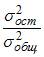характеризует долю …остаточной дисперсии
4. В случае, если общая сумма квадратов отклонений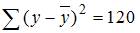 
, и остаточная сумма квадратов отклонений 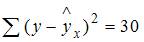, то сумма квадратов отклонений, растолкованная регрессией, равна …90
1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой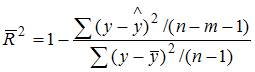 
, где …
n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
2. В случае, если известно уравнение множественной регрессии выстроенное по итогам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равняется …766,67
3. Для регрессионной модели известны следующие размеры дисперсий:
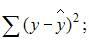
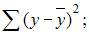
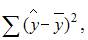где y – значение зависимой переменной по исходным данным; – значение зависимой переменной, вычисленное по регрессионной модели; – среднее значение зависимой переменной, определенное по исходным статистике. Для указанных дисперсий справедливо равенство …
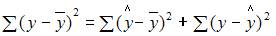
1. Для уравнения множественной регрессии вида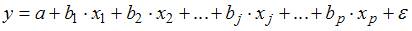 
на основании 14 наблюдений вычислены оценки параметров и записана модель: 
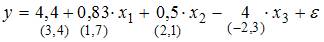(в скобках указаны значения t-статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для разных уровней значимости
При уровне значимости 0,1 значимыми являются параметры …
2. В случае, если для значения оценки и среднеквадратической ошибки параметра этого параметра линейной эконометрической модели выполняется соотношение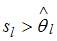 
, то это говорит о статистической ______ параметра.ненадежности оценки
3. Для уравнения множественной регрессии вида 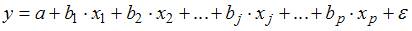на основании 14 наблюдений вычислены оценки параметров и записана модель: 
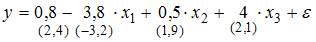(в скобках указаны значения t-статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для разных уровней значимости
Для данного уравнения при уровне значимости ?=0,05 значимыми являются параметры …
4. Проверка статистически значимого отличия от нуля оценок коэффициентов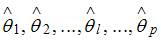 
линейной модели
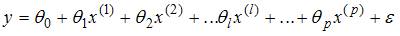
осуществляется методом последовательного сравнения взаимоотношений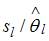 
( –среднеквадратическая неточность параметра ) с точкой, имеющей распределение …Стьюдента
1. В случае, если связь объема между цены и спроса характеризуется постоянной эластичностью, то моделирование целесообразно проводить на базе …степенной функции
2. В случае, если по итогам анализа поля корреляции увидено, что на промежутке трансформации фактора изменяется темперамент связи разглядываемых показателей, связь изменяется на обратную, то моделирование целесообразно проводить на базе …параболы второй степени
3. Нелинейное уравнение регрессии вида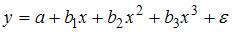 
есть _____ моделью ________ регрессии.полиномиальной … парной
4. В случае, если с повышением масштабов производства удельный расход сырья уменьшается, то моделирование целесообразно проводить на базе …равносторонней преувеличения
1. Степенной моделью не есть регрессионная модель …
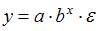
2. Среди предложенных нелинейных зависимостей нелинейной по параметрам есть …
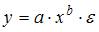
3. Среди предложенных нелинейных зависимостей нелинейной значительно (внутренне нелинейной) есть …
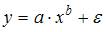
4. Среди предложенных нелинейных зависимостей внутренне линейной есть …
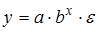
1. Для линеаризации нелинейной регрессионной модели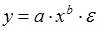 
употребляется …логарифмирование
2. Для преобразования внутренне нелинейной функции 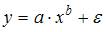возможно применен способ …разложения функции в ряд Тейлора
3. Для линеаризации нелинейной функции 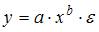возможно применен замены …и метод логарифмирования переменных
1. При расчете уравнения нелинейной регрессии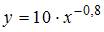 
, где y – спрос на продукцию, ед.; x – цена продукции, руб., стало известно, что часть остаточной дисперсии в общей меньше 20%. Коэффициент детерминации для данной модели попадает в отрезок минимальной длины …[0,8; 1]
2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к прошлому году) и выстроено уравнение в логарифмах исходных показателей: . Коэффициент корреляции между логарифмами исходных показателей составил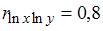 
. Коэффициент детерминации для модели в исходных показателях равен …0,64
3. Для регрессионной модели , где – нелинейная функция, – вычисленное по модели значение переменной , взяты значения дисперсий: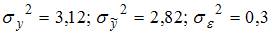 
. Не растолкована моделью часть дисперсии переменной , равная …0,096
4. Для регрессионной модели , где – нелинейная функция, – вычисленное по модели значение переменной , получено значение индекса корреляции R = 0,64. Моделью растолкована часть дисперсии переменной , равная …
5. По итогам проведения изучения торговых точек было выстроено уравнение нелинейной регрессии 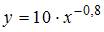, где y – спрос на продукцию, ед.; x – цена продукции, руб. В случае, если фактическое значение t-критерия Стьюдента образовывает –2,05, а критические значения для данного количества степеней свободы равны 
, 
, 
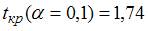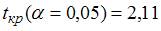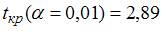, то …при уровне значимости можно считать, что эластичность спроса по цене образовывает –0,8
1. В состав любого временного последовательности, выстроенного по настоящим данным, непременно входит _____ компонента.случайная
3. Совокупность значений экономического показателя за пара последовательных моментов (периодов) времени именуется …временным рядом
1. Значение коэффициента автокорреляции первого порядка характеризует …тесноту линейной связи