ТЕМА 10. Изучаемые вопросы: Построение трендовых моделей при помощи диаграмм в среде MIKROSOFT EXCEL;Коэффициент достоверности аппроксимации R2
Аппроксимация данных функции способом мельчайших квадратов
Цель:Выстроить кривые, аппроксимирующие с заданной точностью данные, полученные на протяжении экспериментального изучения.
В качестве данных имеем значения ежемесячного износа тормозных колодок автомобиля. Данные представлены в виде, графика (рис. 32) складывающегося из 10 результатов измерений износа (по месяцам).
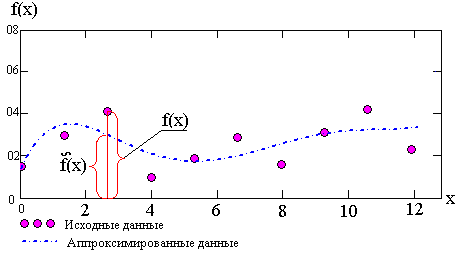
Рис.32. График износа тормозных колодок автомобиля (по месяцам года)
Разглядываемый процесс колебания ежемесячного износа тормозных колодок имеет моменты пиков и спадов. Это разъясняется тем что, износ нестабилен по времени, поскольку зависят от пробега, климатических и дорожных условий и т.п., соответственно, есть случайной величиной. Поэтому эргономичнее будет трудиться с аппроксимированными параметрами модели.
Аппроксимацию выполним способом мельчайших квадратов.
Пускай …, — последовательность линейно-свободных функций на [a,b]. Аппроксимирующую функцию будем воображать в виде:
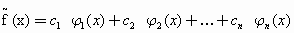(56)
где с1,с2,…..,сn — малоизвестные параметры функции .
Тогда, в соответствии с способу мельчайших квадратов, функционал J, имеющий суть суммы квадратов отклонений аппроксимирующей функции от результатов измерений в заданных точках запишется в виде:
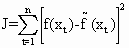(57)
и параметры с1,с2,…..,сn будем выбирать из условия минимума этого функционала, т.е.
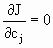, j=1,n. (58)
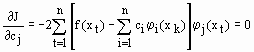(59)
либо
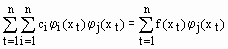, j=1,n (60)
Последнее выражение возможно записать в виде совокупности линейных алгебраических уравнений довольно малоизвестных параметров с1,с2,…..,сn .
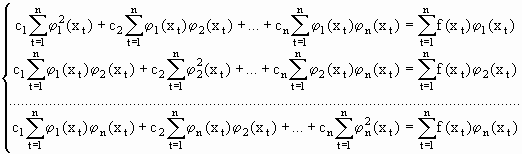(61)
либо в матричной форме:
, (62)
где: A – симметрическая матрица порядка n; – n мерный вектор-столбец свободных участников; – n мерный вектор-столбец малоизвестных параметров, каковые возможно представить в виде:
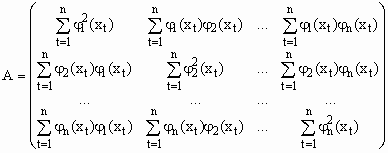, (63)
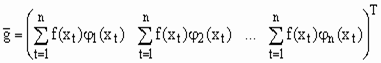, (64)
(65)
Так, задача нахождения параметров аппроксимирующей функции (42) сводится к ответу совокупности линейных алгебраических уравнений (48). Это возможно сделать двумя методами:
1. или искать ответ совокупности (45);
2. или обнаружить матрицу , обратную матрице A, тогда
(66)
Как правило (в зависимости от вида конкретных матриц) при аппроксимации комфортно придерживаться второго пути. В качестве последовательности …, — забраны величины: (1, X, X2, …….Xn).
ПОСТРОЕНИЕ ТРЕНДОВЫХ МОДЕЛЕЙ ПРИ ПОМОЩИ ДИАГРАММ
Многие экспериментальные эти возможно трактовать как временные последовательности — последовательность измерений, взятых в определенные моменты времени ti, где i — порядковый номер измерения на оси времени. Такие последовательности характеризуются некоей тенденцией развития процесса во времени и именуются трендовыми. Применяя трендовые модели, возможно выдавать прогнозы на кратковременный и среднесрочный периоды. Excel имеет средства для трендовых моделей встроенные в построитель диаграмм.
Одной из форм трендовых моделей при постоянном шаге по времени есть линейная модель:
(67)
Как пример используем информацию о динамике трансформации числа машин в АТП с 2000 по 2010 гг. Знание данной динамики разрешает планировать развитие АТП и его инфраструктуры на возможность. Данные приведены в таблице 3. Таблица 3.
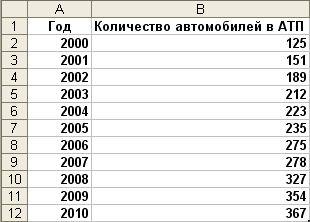
Порядок расчетов следующий.
1. Выделить диапазон B2:B12 и выстроить согласно этой информации диаграмму типа График, щелкнув по значку Мастер диаграмм на панели инструментов.
2. Выделить диаграмму и выполнить Диаграмма/Добавить линию тренда.
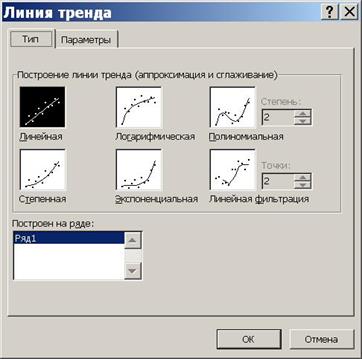
3. В окне Линия тренда открыть вкладку Параметры и установить флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации.
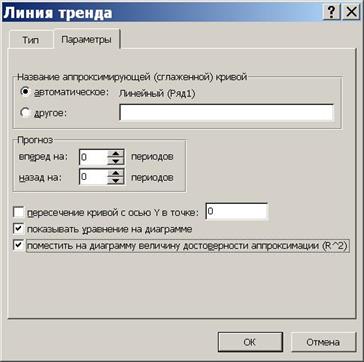
4. На вкладке Тип выбрать тип диаграммы – линейная и надавить Ok. Результаты продемонстрированы на рисунке.
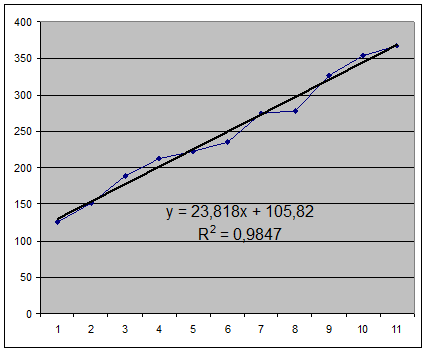
5. Вычислить по формуле y = 23,818x + 105,82. направляться учесть, что доводом трендовой модели есть порядковый номер, какое количество.е. в отечественном примере x=12. В следствии возьмём прогноз на 2011 год: 391 автомобиль.
Коэффициент достоверности аппроксимации R2 показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R2 к 1, тем правильнее модель обрисовывает имеющиеся эти.
Быть может, что более надежный прогноз был бы взят посредством степенной либо экспоненциальной линий тренда. Исходя из этого разглядим еще один пример применения нелинейного тренда.
В ходе трансформации угла опережения зажигания у двигателя автомобиля ГАЗ-3307 осуществляли контроль часовой расход горючего. Регулировку делали на стенде тяговых качеств. Значения угла опережения зажигания Х и значения часового расхода горючего записывали в таблицу 4.
Таблица 4.
| Х | |||||||
По окончании чего результаты измерений были занесены в таблицу 5 среды Микрософт Excel:
Таблица5.
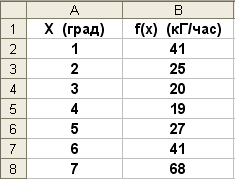
Рис. 33. Внешний вид таблицы 1 в среде Микрософт Excel
Выделим диапазон А2:B8 и выстроим согласно этой информации диаграмму типа Точечная, щелкнув по значку Мастер диаграмм на панели инструментов.
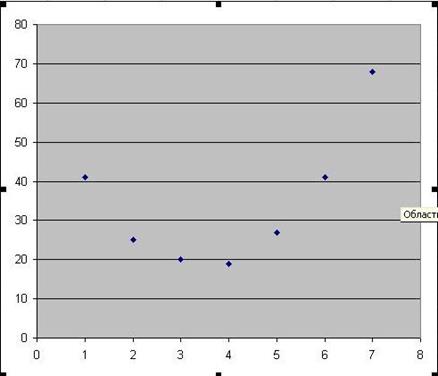
Рис. 34 Внешний вид графика функции в среде Микрософт Excel
Выделим диаграмму и выполним Диаграмма/Добавить линию тренда. (см. рис. 35).
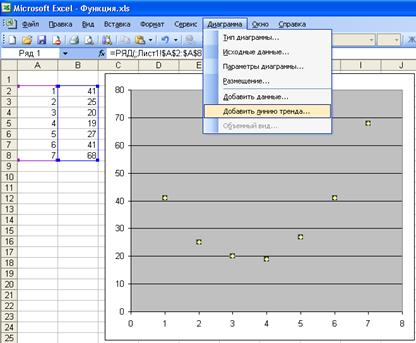
Рис. 35. Опция добавления линии тренда на график функции
В окне Линия тренда открыть вкладку Параметры и установить флажки Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (см. рис. 34 и 35).
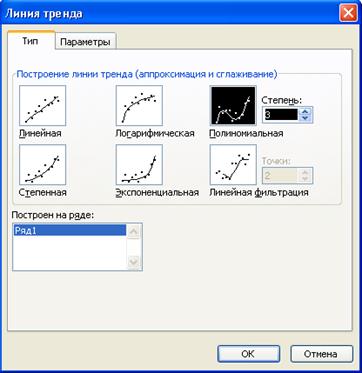
Рис. 36. Опция добавления линии тренда на график функции
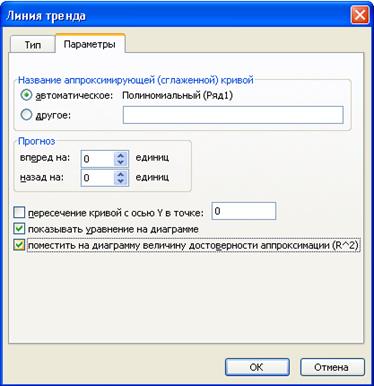
Рис. 37 Опция добавления уравнения графика функции
На вкладке Тип выбрать тип диаграммы – «Полиномиальная» и надавить Ok. Результаты продемонстрированы на рисунке 36.
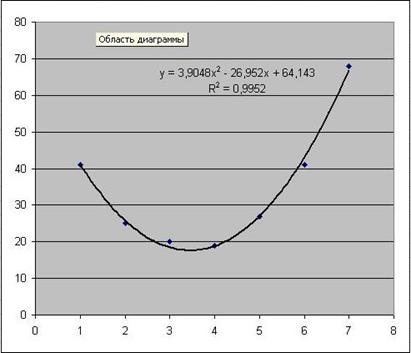
Рис. 38 уравнение и График функции
Полученное уравнение y = 3,9048×2 – 26,952x + 64,143 зависимости часового расхода горючего от величины угла опережения зажигания с достоверностью аппроксимации R2 = 0,9952 разрешает выяснить оптимальный для данного автомобиля угол опережения зажигания (на уровне 3,5о), снабжающий минимум часового расхода горючего.
РЕГРЕССИОННЫЙ АНАЛИЗ
ТЕМА 11. Изучаемые вопросы. Методика проведения регрессионного анализа; Построение модели множественной регрессии в среде MIKROSOFT EXCEL.
Регрессионный анализ дает возможность приобрести функциональную зависимость между некоей случайной величиной Y и некоторыми воздействующими на Y размерами X. Такая зависимость стала называться уравнения регрессии. Различают несложную (парную) и множественную регрессию линейного и нелинейного типа.
Пример несложной линейной регрессии имеет форму:
y = m1x+b.
Пример множественной линейной регрессии:
y = m1x1 + m2x2 + … + mkxk + b. (68)
Для оценки степени связи между размерами, входящими в уравнение (54) употребляется коэффициент множественной корреляции R Пирсона (корреляционное отношение), что может принимать значения от 0 до 1. R=0 в случае, если между размерами нет никакой связи и R=1, в случае, если между размерами имеется функциональная (детерминированная) сообщение. Как правило R принимает промежуточные значения от 0 до 1. Величина R2 именуется коэффициентом детерминации.
Задачей построения регрессионной зависимости есть нахождение вектора коэффициентов M модели (54) при котором коэффициент R принимает большое значение.
Для оценки значимости R используется F-критерий Фишера, вычисляемый по формуле:
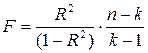, (69)
где n — размер выборки (количество опытов); k — число коэффициентов модели. В случае, если F превышает некое критическое значение для данных n и k и принятой доверительной возможности, то величина R считается значительной. Таблицы критических значений F приводятся в справочниках по математической статистике.
Так, значимость R определяется не только его величиной, но и соотношением между количеством коэффициентов и количеством экспериментов (параметров) модели. Вправду, корреляционное отношение для n=2 для несложной линейной модели равняется 1 (через 2 точки на плоскости возможно постоянно провести единственную прямую). Но в случае, если экспериментальные эти являются случайными размерами, доверять такому значению R направляться с громадной осторожностью. В большинстве случаев для получения значимого R и точной регрессии стремятся к тому, дабы количество опытов значительно превышало количество коэффициентов модели (nk).
Для построения линейной регрессионной модели нужно:
1) подготовить перечень из n строчков и m столбцов, содержащий экспериментальные эти (столбец, содержащий выходную величину y должен быть или первым, или последним в перечне);
2) обратиться к меню Сервис/Анализ данных/Регрессия
В случае, если пункт Анализ данных в меню Сервис отсутствует, то направляться обратиться к пункту Надстройки того же меню и установить флажок Пакет анализа.
3) в диалоговом окне Регрессия задать:
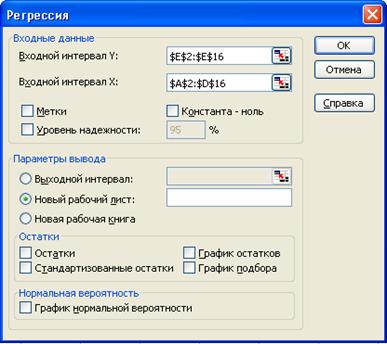
- входной промежуток Y;
- входной промежуток X;
- выходной промежуток — верхняя левая ячейка промежутка, в который будут помещаться результаты вычислений (рекомендуется разместить на новом рабочем странице);
4) надавить Ok и проанализировать результаты.
Пример применения множественной линейной регрессии
Предположим, что нужно дать среднестатистический прогноз путевого расхода горючего автомобиля. Для этого имеется возможность воспользоваться множественным регрессионным анализом (на базе анализа параметров солидного числа машин) для оценки расхода горючего Q [л/100 км], с применением следующих переменных (параметров):
m1 – Количество двигателя автомобиля [см3];
m2 – Масса автомобиля [кГ];
m3 – Тип привода, определяемый числом ведущих колес [2 либо 4];
m4 – Мощность двигателя [л.с.].
В этом примере предполагается, что существует линейная зависимость между каждой свободной переменной (m1, m2, m3 и m4) и зависимой переменной (Q), другими словами расходом горючего. Данные продемонстрированы на рисунке.
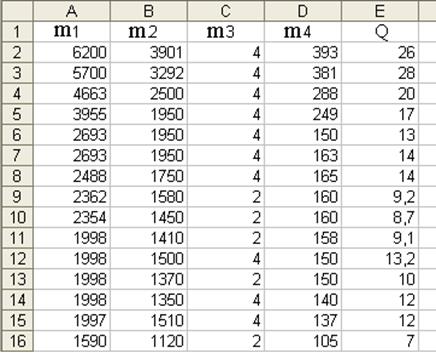
Настройки для ответа поставленной задачи продемонстрированы на рисунке окна Регрессия. Результаты расчетов размещены на отдельном странице в таблице 6.
В итоге взята следующая математическая модель:
Q = -0,002159246·x1 + 0,001581937·x2 + 1,987200675·x3 + 0,078512695·x4- 4,428016498
Сейчас возможно выяснить примерный расход горючего у автомобиля с колёсной формулой и бензиновым двигателем 4 ? 4, в случае, если как мы знаем, что двигатель автомобиля имеет количество 2700 см3, его масса образовывает 1950 кг, автомобиль имеет полный привод на колеса – 4 ведущих колеса, мощность двигателя образовывает 163 л.с., применяя следующую формулу:
Q = -0,002159246·2700 — 0,001581937·1950 + 1,987200675·4 + 0,078512695·163- 4,428016498
Решив это уравнение, приобретаем расход горючего у данного автомобиля: Q = 13,57 л/100 км.
В регрессионном анализе самые важными результатами являются:
- коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели;
- множественный коэффициент R, характеризующий точность
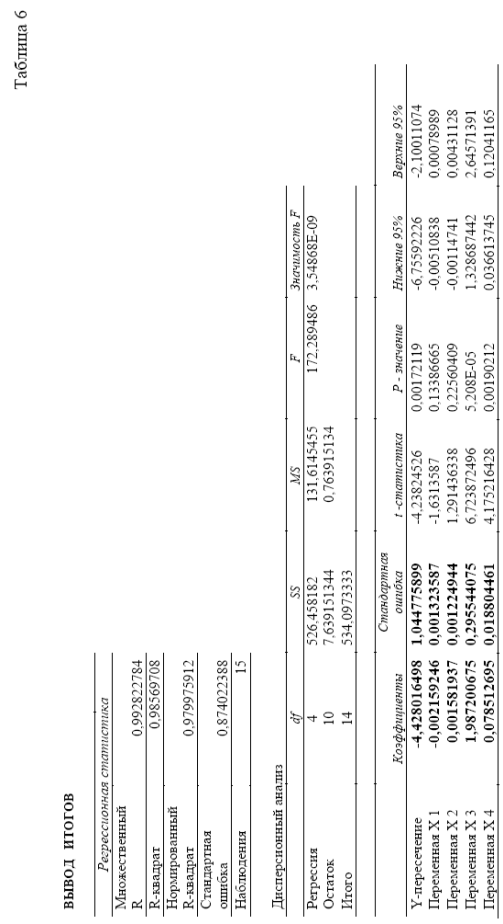
модели для имеющихся данных;
- F-критерий Фишера (в рассмотренном примере он существенно превосходит критическое значение, равное 3,54868E-09);
- t-статистика– величины, характеризующие степень значимости отдельных коэффициентов модели.
На t-статистике направляться остановиться очень. Часто при построении регрессионной модели неизвестно, воздействует ли тот либо другой фактор Х на Y. Включение в модель факторов, каковые не воздействуют на выходную величину, ухудшает уровень качества модели. Вычисление t-статистики оказывает помощь найти такие факторы. Приближенную оценку возможно сделать так: в случае, если при nk величина t-статистики по безотносительному значению намного больше трех, соответствующий коэффициент нужно считать значимым, а фактор включить в модель. В другом случае его нужно исключить из модели. Так, возможно предложить разработку построения регрессионной модели, складывающуюся из двух этапов:
1) обработать пакетом Регрессия все имеющиеся эти, проанализировать значения t-статистики;
2) удалить из таблицы данных столбцы с теми факторами, для которых коэффициенты незначимы, и обработать пакетом Регрессия новую таблицу.
Для примера разглядим переменную m4. В справочнике по математической статистике t-критическое с (n-k-1) = 15-5-1=9 доверительной вероятностью и степенями свободы 0,95 равняется 2,26. Потому, что полная величина t, равная 4,17 больше, чем 2,26, мощность двигателя — это ответственная переменная для оценки расхода горючего. Подобным образом возможно протестировать все другие переменные на статистическую значимость. Ниже приводятся замечаемые t-значения для каждой из свободных переменных:
| Количество двигателя | 1,6313587 |
| Масса автомобиля | 1,2914363 |
| Тип привода | 6,7238724 |
| Мощность двигателя | 4,1752164 |
Из таблицы видно, что значения «Мощности двигателя – m4» и «Типа привода – m3» имеют полную величину громадную, чем 2,26 следовательно, эти переменные, использованные в уравнении регрессии, нужны для предсказания путевого расхода горючего автомобиля. А такие значения как «Масса автомобиля – m2» и «Количество двигателя – m1» имеют безотносительную величину меньшую чем 2,26. Следовательно, эти переменные, использованные в уравнении регрессии, нужно исключить из модели. Это разрешит повысить уровень качества предсказания путевого расхода горючего автомобиля.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что именуется научным изучением;
2. Что есть объектом научного изучения. Приведите примеры;
3. Что включает структура объекта научного изучения;
4. постановка задач и Формулирование цели научного изучения. Приведите примеры;
5. Какие конкретно виды научных изучений Вы понимаете. Поясните их сущность, преимущества и недочёты;
6. Структура экспериментального научного изучения;
7. Какие конкретно методики включает в себя экспериментальное научное изучение;
8. Поясните цель и содержание методики планирования экспериментального изучения;
9. Как выяснить количество выборки способом проверки статистических догадок;
10. тестовые возможности и Устройство стендов с беговыми барабанами в ходе экспериментальных изучений на автомобильном транспорте;
11. тестовые возможности и Устройство стендов для изучения черт шин;
12. тестовые возможности и Устройство стендов для задания тестовых режимов при изучении автомобильного двигателя;
13. Структура аналитического научного изучения на автомобильном транспорте;
14. Какое оборудование для задания тестовых режимов объектам изучения на автомобильном транспорте Вы понимаете;
15. Как устанавливаются причинно-следственные связи на структурной схеме объекта изучения;
16. Как разрабатывается математическая модель исследуемого процесса;
17. Как осуществляется настройка и проверка адекватности математической модели;
18. Какие конкретно вопросы разрешает решать регрессионный анализ в ходе научных изучений на автомобильном транспорте;
19. Как выстроить модель множественной регрессии в среде MIKROSOFT EXCEL.
20. Начертите схему и поясните сущность измерения сил тензометрическим способом;
21. Начертите схему и поясните сущность измерения давления;
22. Начертите схему и поясните сущность измерения моментов силы тензометрическим способом;
23. Как калибруется совокупность измерения сил;
24. Начертите схему и поясните сущность измерения промежутков времени цифровым способом;
25. Начертите схему и поясните сущность измерения скорости вращения;
26. Начертите схему и поясните сущность измерения угла поворота вала;
27. Начертите схему и поясните сущность измерения угла поворота коленчатого вала двигателя;
28. Начертите схему и поясните сущность измерения температуры при помощи сопротивления термопреобразователя;
29. Начертите схему и поясните сущность измерения температуры при помощи термоэлектрического преобразователя (термопары);
30. Анализ температурных полей при помощи тепловизора;
31. Начертите схему и поясните сущность стробоскопического способа измерения угла опережения зажигания;
32. Начертите схему и поясните сущность гироскопического способа измерения углов;
33. Начертите схему и поясните работу расходомера горючего ротационного типа;
34. Начертите схему и поясните работу расходомера горючего объемного типа;
35. Начертите схему расходомера горючего объемного типа и поясните принцип его работы при измерении «мгновенного» и «путевого» расхода горючего;
36. Как осуществляется тарировка расходомера горючего;
37. Дайте определения понятию «безотносительная погрешность измерения». Как она определяется;
38. Дайте определения понятию «относительная погрешность измерения». Как она определяется;
39. Погрешности измерений. Как определяются полная и относительная погрешности измерения силы тензометрическим способом;
40. Какое оборудование для визуализации результатов измерений Вы понимаете;
41. Как устроен и как трудится электронно-лучевой осциллограф;
42. Как осуществляется калибровка вертикальной шкалы электронно-лучевого осциллографа;
43. Как осуществляется калибровка горизонтальной шкалы электронно-лучевого осциллографа;
44. Аналого-цифровое преобразование. Приведите схему процесса и дайте пояснение;
45. Поясните способ кодирования чисел в виде единиц и сочетания нулей. Дайте определение понятию «логическая единица» и «логический ноль»;
46. Как строится кривая и гистограмма распределения случайной величины;
47. Как осуществляется обработка результатов измерений;
48. Как осуществляется анализ результатов экспериментального изучения;
49. Как выполняется аппроксимация данных функции с применением способа мельчайших квадратов;
50. Как аппроксимировать результаты экспериментального изучения в среде MIKROSOFT EXCEL. Дайте определение понятию «аппроксимация»;
51. Поясните сущность коэффициента достоверности аппроксимации R2;
52. Перечислите статистические характеристики случайной величины.
Перечень главной литературы:
1. Диагностика автомобиля: Учебник для институтов. // Федотов А.И., Изд-во ИрГТУ, Иркутск. 2012. 463 с. Ил. 273. Табл. 22. Библиограф.: 64 назв.
2. Электрические измерения физических размеров: Способы измерения: Учебное пособие для институтов // С.А.Спектор., : Л. Энергоатомиздат. Ленинградское отделение,1987.- 320 с.
3. Базы разработки полигонных опробований и сертификация машин // Безверхий С.Ф., Яценко Н.Н., М.: ИПК Издательство стандартов, 1996. – 600
4. долговечность и Прочность автомобиля // Под неспециализированной ред. Б.В. Гольда, М., Машиностроение, 1974. 328 с., ил.
5. проверка гипотез и Статистическое оценивание на ЭВМ // Петрович М.Л., Давидович М.И. — М.: статистика и Финансы,1989. -191 с.: ил. (Мат. обеспечение прикладной статистики).
6. Способы оптимизации. Вводный курс // Банди Б.: Пер. с англ. – М.: Радио и сообщение, 1988. – 128 с.: ил.
7. Способы оптимизации в технической диагностике автомобилей // Харазов А.М., Цвид С.Ф. М.: Машиностроение, 1983. – 132 с., ил.
8. анализ и Планирование эксперимента данных // Монтгомери Д., Пер. с англ. – Л.: Судостроение, 1980. – 384 с., ил.
9. Способы обработки экспериментальных данных при измерениях // Грановский В.А., Сирая Т.Н., Энергоатомиздат. Ленингр. отд-ние, 1990. – 288 с.: ил.
10. Шор. Я. Б. Статистические способы анализа и надёжности и контроля качества. М.: Госэнергоиздат, 1962, с. 552, С. 92-98.
Перечень дополнительной литературы:
11. Диагностическое обеспечение ремонта автомобилей и технического обслуживания: Справ. пособие. – М.: Высш. шк., 1990. – 208 с.: ил.
12. Опробование машин // Учебник для машиностроительных техникумов по профессии «Автомобилестроение» / Балабин И.В., Куров Б.А., Лаптев С.А. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1988. – 192 с.: ил.
13. Технологическое оборудование для ремонта и технического обслуживания автомобилей : Справочник/ Р.А. Попржедзинский, А.М. Харазов и др. – М.: Транспорт, 1988. – 176 с., ил., табл.
14. Измерения в электро- и радиотехнике: Учеб. Пособие. для средн. проф.-техн. училищ. – М.: Выс. шк., 1984. – 207 с., ил.
ОГЛАВЛЕНИЕ
| Тема 1. Методологические базы творчества и научного познания ………………………… | |
| постановка задач и Формулирование цели изучения….……………………………………… | |
| Тема 2. Теоретические и эмпирические способы изучения………………………………… | |
| Тема 3.Методика планирования экспериментального изучения ………………………….. | |
| Тема 4.Оборудование для задания тестовых режимов…………………………………………….. | |
| Тема 5.системы и Измерительные приборы, применяемые при проведении научных изучений …………………………………………………………………..………………………………. | |
| Измерение сил посредством тензорезисторного моста ……………………………………………… | |
| Измерение крутящего момента …………………………………………..………………………………. | |
| Тарировка тензометрических измерителей силовых параметров ………………………………. | |
| Тарировка тензометрических измерителей крутящего момента ………………………….…… | |
| Измерение давления …………………………………………………………………….…………………… | |
| Измерение промежутков времени …………….……………………………………….…………………… | |
| Измерение скорости вращения ……………………………………..……………….……………………. | |
| Измерение угла поворота вала ……………………………………………………………………………. | |
| Измерение скорости вращения коленчатого вала……………………………………………………. | |
| Измерение температуры…………………………………………………………….……………………. . | |
| Термопреобразователи сопротивления…………………………………………………………….…… | |
| Термоэлектрические преобразователи…………………………………………………………….……… | |
| Анализ температурных полей…………………………………………………………….………………… | |
| Стробоскопический способ измерения угла опережения зажигания………….………………… | |
| Гироскопический способ измерения углов…………………………………………….…………………. | |
| Измерение расхода горючего расходомером ротационного типа……………….………………… | |
| Измерение расхода горючего расходомером поршневого типа ………………….………………. | |
| Измерение мгновенного расхода горючего .…………………………………………….……………… | |
| Измерение путевого расхода горючего .…………………………………………….…………………… | |
| Тарировка расходомеров горючего.………………………………………….…………………………… | |
| Тема 6.Оборудование для визуализации результатов измерений …………………….…………. | |
| Тема 7.Аналого-цифровое преобразование измеряемых сигналов ……………………………. | |
| Метрологические характеристики аналого-цифрового преобразования ……………………… | |
| ТЕМА 8. методология и Теория научного творчества …………………………….. | |
| Прикладные способы математической обработки экспериментальных данных ………………. | |
| ТЕМА 9. Аналитические научные изучения на автомобильном транспорте ……………. | |
| Проверка адекватности математической модели ……………….……………….……………….…. | |
| Тема10. Аппроксимация данных с применением способа мельчайших квадратов ……. | |
| Построение трендовых моделей при помощи диаграмм ………………………………………….. | |
| Коэффициент достоверности аппроксимации R2…………………………………………………….. | |
| Тема11. Регрессионный анализ ………………………………………………………………………….. | |
| Контрольные вопросы ………………………………………………………………………………………. | |
| Перечень литературы…………………………………………………………………………………………… | |
| Оглавление |
Федотов Александр Иванович
БАЗЫ НАУЧНЫХ ИЗУЧЕНИЙ
Учебно-методическое пособие
для студентов институтов, обучающихся по профилю «Эксплуатация транспортно-технологических автомобилей и комплексов», направления подготовки 190600.62 эксплуатация транспортно-технологических автомобилей и комплексов, квалификации – «бакалавр», и 190600.68 степени — «магистр»
Подписано в печать 2012. Формат 60х84 1/16
Бумага типографская. Печать офсетная. Усл. печ. л. 6,25
Уч.- изд. л. 5,9 Тираж 200 экз. Зак
ИД № 06506 от 26.12.2001
Иркутский национальный технический университет
664074, Иркутск, ул. Лермонтова, 83
[1] Подробное описание принципа измерений с применением мостовой схемы приведено на стр. 26 ? 30
[2] Детально работа электронно-лучевой трубки обрисована в следующем разделе «Тема 6»
[3] МЗР — дискретность квантования либо младшее значение разряда, определяется как отношение амплитуды измеряемого сигнала на количество уровней квантования N=2n, которое при бинарном коде, и разрядности n=12 бит, N=4096.