Теоретические сведенья
Способ конфигураций
Способ конфигураций, помогает для поиска абсолютного локального экстремума функции и относится к прямым способам, другими словами опирается конкретно на значения функции. Метод делится на две фазы: исследующий поиск и поиск по примеру.
На начальной стадии задается стартовая точка (обозначим её h1) и шаги hi по координатам. После этого замораживаем значения всех координат не считая 1-й, вычисляем значения функции в точках x0+h0 и x0-h0 (где x0 — первая координата точки, а h0 — соответственно значение шага по данной координате) и переходим в точку с мельчайшим значением функции. В данной точке замораживаем значения всех координат не считая 2-й, вычисляем значения функции в точках x1+h1 и x1-h1, переходим в точку с мельчайшим значением функции и т. д. для всех координат. , если для какой-нибудь координаты значение в исходной точке меньше, чем значения для обоих направлений шага, то ход по данной координате значительно уменьшается. В то время, когда шаги по всем координатам hi станут меньше соответствующих значений ei, метод завершается, и точка 1 признаётся точкой минимума.
Так, совершив исследующий поиск по всем координатам, мы возьмём новую точку, с мельчайшим значением функции в окрестности (обозначим ее 2). Сейчас возможно осуществлять переход ко 2 фазе метода.
На этапе поиска по примеру откладывается точка 3 в направлении от 1 к 2 на том же расстоянии. Её координаты получаются по формуле, где xi — точка с номером i, ? — параметр метода, в большинстве случаев выбирающийся равным 2. После этого в новой точке 3 проводится исследующий поиск, как на 1 фазе метода, за исключением того, что ход на данной фазе не значительно уменьшается. В случае, если на данной фазе, в следствии исследующего поиска, удалось взять точку 4, хорошую от точки 3, то точку 2 переобозначим на 1, а 4 на 2 и повторим поиск по примеру. В случае если не удаётся отыскать точку 4, хорошую от точки 3, то точку 2 переобозначим на точку 1 и повторим 1-ю фазу метода — исследующий поиск.
Способ Ньютона
Способ Ньютона — это итерационный численный способ нахождения корня (нуля) заданной функции. Способ был в первый раз предложен британским физиком, астрономом и математиком Исааком Ньютоном (1643—1727). Поиск ответа осуществляется путём построения последовательных приближений и основан на правилах несложной итерации. Способ владеет квадратичной сходимостью. Улучшением способа есть способ касательных и хорд. Способ Ньютона по большей части употребляется для ответа задач оптимизации, в которых требуется выяснить нуль первой производной или градиента при многомерного пространства.
Стратегия способа Ньютона пребывает в построении последовательности точек, таких, что значение функции в прошлой точки больше, чем в последующей. Точки последовательности выбираются по правилу: . Начальная точка задается пользователем, а направление спуска определяется по формуле , где Н(х) – матрица Гессе, — градиент исходной функции.
Метод работы программы
Ход 1. Пользователь выбирает способ нахождения минимума функции, и вид данной функции из предложенных.
а) При выборе способа Хука – Дживса:
1. Задаем функцию зависимости от двух доводов.
Пользователь задает начальные значения: начальную точку, шаги по координатным направлениям: , неточность , коэффициент уменьшения шага .
2. Осуществляем следующий поиск по выбранному координатному направлению:
а) в случае, если : , то ход считается успешным. В этом случае направляться положить и переходим к шагу 3;
б) в случае, если в п. а ход неудачный, то делается ход в противоположное направление. В случае, если , то положим и перейдем к шагу 3.
3. Удостоверимся в надежности условие: в случае, если , то перейдем к шагу 4, в противном случае, к шагу 5.
4. Совершить поиск по примеру. Положить , и перейти к шагу 2.
а) в случае, если все шаги по координатным направлениям меньше числа , то поиск закончен
б) для тех i, для которых больше , уменьшить величину шага на a перейти к шагу 2.
б) При выборе способа Ньютона
1. Задаем значения нулевой точки, неточность .
2. Находим матрицу Гессе Н(х) и градиент.
3. Положим к = 0, и вычислим градиент в точке .
4. Проверить исполнение критерия окончания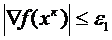 
а) В случае, если неравенство выполнено, то расчет окончен и
б) В случае, если нет, то перейти к пункту 5.
5. Вычислить матрицу .
6. Вычислить матрицу .
7. Проверить исполнения условия 0
а) в случае, если да, то перейти к шагу 9
б) в случае, если нет, то перейти к шагу 10, положив
8. Выяснить
9. Отыскать точку , t=1, в случае, если 0, в противном случае выбрать t из дополнительных условий.
10. В случае, если условие выполняется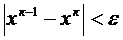 
, поиск окончен, в другом случае положить к = к + 1, и перейти к пункту 3.
Ход 2. Выводим полученные значения точек, и значения функции в этих точках.
Ход 3. Нарисовать линии уровней заданной функции и итерационную процедуру поиска минимума.