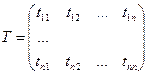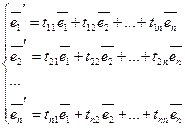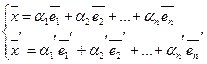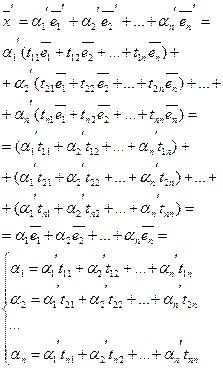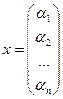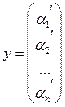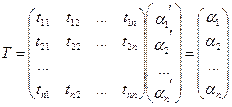Способ Гаусса.
Сперва направляться привести совокупность к треугольному (ступенчатому) виду, а после этого ступенчато решить.
Формула Крамера.
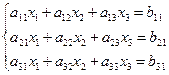
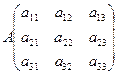
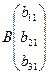
Подсчитать определитель матрицы А.
После этого матрицей B заменить первый столбец матрицы А, подсчитать определитель и поделить его на detA, так мы возьмём x1. То же самое выполнить со 2-ым и 3-им столбцом.
Ответ произвольных совокупностей. Теорема Кронекера-Капелли.
Совокупность линейных алгебраических уравнений совместна тогда и лишь тогда, в то время, когда ранг расширенной матрицы совокупности равен рангу главной матрицы.
Отыскать какой-либо базовый минор порядка r. Забрать r уравнений, из которых составлен базовый минор. Малоизвестные, коэффициенты которых входят в базовый минор, именуются главными и остаются слева, а остальные именуются свободными и переносятся в правую часть уравнения. Отыскав главные через свободные, возьмём неспециализированное ответ совокупности.
Однородные совокупность уравнений. Фундаментальная совокупность ответов.
Совокупность однородных уравнений постоянно имеет нулевое ответ. В случае, если ранг матрицы меньше числа малоизвестных, то совокупность имеет очень много ответов. Чтобы совокупность имела ненулевые ответы, нужно, дабы ее определитель был равен нулю.
Линейные пространства. независимость системы и Линейная зависимость векторов. базис и Размерность линейного пространства.
Разглядим непустое множество элементов, каковые будем обозначать через x, y, z, … и множество настоящих чисел. На этом множестве введем две операции (умножение и сложение). Пускай эти две операции подчиняются теоремам:
1.
2.
3.
4.
5.
6.
7.
8.
V; x, y, z, … V
Множество V с двумя операциями, удовлетворяющее теоремам именуется линейным пространством.
Элементы линейного пространства именуются векторами, обозначаются , , . Существует единственный нулевой элемент, для каждого элемента существует единственный противоположный.
независимость системы и Линейная зависимость векторов. Пускай имеется n векторов.
Составим линейную комбинацию:
, в случае, если совокупность n векторов – линейно-зависима.
В случае, если среди n векторов какие-то k линейно-зависимы, то вся совокупность векторов есть линейно-зависимой.
В случае, если совокупность n векторов линейно-свободна, то одна из частей из этих векторов будет также линейно-свободной.
базис и Размерность линейного пространства. Пускай совокупность n векторов линейно-свободна, а каждая совокупность n+1 векторов – линейно-зависима, тогда число n именуют размерностью пространства. dimV=n
Совокупность этих n линейно-свободных векторов именуется базисом линейного пространства. Разглядим совокупность n+1 векторов.
Такое представление именуется разложение по базису, а числа именуют координатами вектора.
Разложение любого вектора в выбранном базисе — единственно.
Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.
n – мерное пространство.
Vn – базис, складывающийся из n векторов.
В пространстве имеется базисы
Введем матрицу перехода от к .