Вопросы
Кратные интегралы
1.1 Двойной интеграл: вычисление двойного интеграла в декартовых и в полярных координатах.
1.2 Приложения двойного интеграла к задачам геометрии.
1.3 Тройной интеграл: вычисление тройного интеграла в декартовых, цилиндрических координатах.
1.4 Приложения тройного интеграла к задачам геометрии.
Криволинейные и интегралы
2.1 Криволинейный интеграл 1-го рода: вычисление, приложения и свойства.
2.2 Криволинейный интеграл 2-го рода: свойства, вычисление, приложения. Формула Остроградского-Грина. Условия независимости криволинейного интеграла от формы пути на плоскости.
Поверхностные интегралы
3.1 Фундаментальные особенности поверхностного интеграла 1 рода, вычисление.
3.2 Определение поверхностного интеграла 2 рода.
3.3 Фундаментальные особенности поверхностного интеграла 2 рода, вычисление.
3.4 Связь между поверхностными интегралами первого и второго родов.
3.5 Формула Остроградского-Гаусса.
3.6 Формула Стокса.
Теория поля
4.1 Поле. Скалярное поле. Векторное поле.
4.2 Характеристики скалярного поля: линии (поверхности) уровня, градиент, производная по направлению.
4.3 Характеристики векторного поля: векторные линии, дивергенция, поток, циркуляция, ротор, потенциал.
Теория последовательностей
5.1 Числовой последовательность. Сходимость. Неспециализированный член последовательности. Сумма последовательности. Достаточный показатель расходимости. Обобщенно-гармонический последовательность.
5.2 Показатели сходимости: показатели Даламбера, радикальный показатель Коши, интегральный показатель Коши, показатель сравнения.
5.3 Знакочередующиеся последовательности. Безотносительная и условная сходимость. Показатель Лейбница.
5.4 Степенные последовательности: радиус и интервал сходимости. Разложение функции в степенной последовательность. Использование к приближенным вычислениям.
5.5 Последовательность Фурье. Разложение функций в ряд Фурье.
Банк задач
Последовательности
1.1) Написать первые пять участников последовательности по заданному неспециализированному участнику: а) 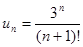 ; б)
; б) 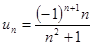 .
.
2) Отыскать суммы последовательностей: а) 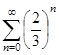 ; б)
; б) 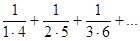 ; в)
; в) 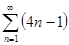 .
.
3) Изучить последовательности на сходимость: а) 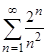 ; б)
; б) 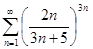 ; в)
; в) 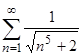 ; г)
; г) 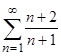 ;
;
д) 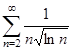 , е)
, е) 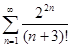 .
.
4) Изучить последовательности на полную сходимость:
а) 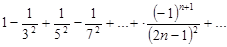 ; б)
; б) 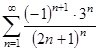 .
.
2.Отыскать область сходимости последовательностей. Узнать сходимость на финишах промежутка сходимости:а) 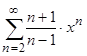 ; б)
; б) 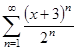 ; в)
; в) 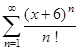 ; г)
; г) 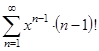 ; д)
; д) 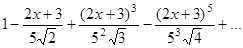
3. 1) Разложить в ряд Маклорена следующие функции (применяя «готовые» разложения):
а) ; б) ; в) ; г) ; д) 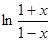 ; е)
; е) 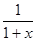 ; ж)
; ж) 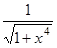 .
.
2) Вычислить приближенно с точностью до 0,001:
а) ; б) ; в) ; г) (выяснив );
ж) 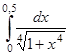 ; з)
; з) 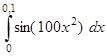 ; и)
; и) 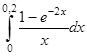 ; к)
; к) 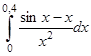 .
.
4. 1) Разложить в ряд Фурье функцию y = 1+ на (-p,p) .
2) Разложить функцию в ряд Фурье y=x-1 , -2 2.
3) Разложить функцию в ряд Фурье y=2x , -1 1.
Кратные интегралы
1.Вычислить:
1) 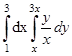 ; 2)
; 2) 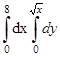 ; 3)
; 3) 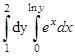 ; 4)
; 4) 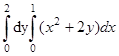 ; 5)
; 5) 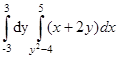 .
.
2.1) Вычислить 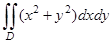 , в случае, если область ограничена линиями y = x, x = 0, y = 1, y = 2.
, в случае, если область ограничена линиями y = x, x = 0, y = 1, y = 2.
2) Вычислить 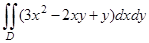 , в случае, если область ограничена линиями х = 0, х = у2, у = 2.
, в случае, если область ограничена линиями х = 0, х = у2, у = 2.
3) Вычислить 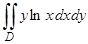 , в случае, если область интегрирования ограничена линиями ху=1, у = , х=2.
, в случае, если область интегрирования ограничена линиями ху=1, у = , х=2.
4) Вычислить 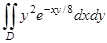 , в случае, если область интегрирования
, в случае, если область интегрирования 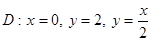 .
.
5) Вычислить 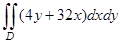 по области D, ограниченной линиями:
по области D, ограниченной линиями:
3.Отыскать площадь плоской фигуры, ограниченной линиями:
1) 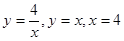 ; 2) ; 3) ;
; 2) ; 3) ;
4)
4.1) Вычислить: 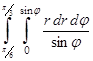 .
.
2) Вычислить 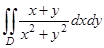 , где ограничена линиями
, где ограничена линиями
3) Вычислить интеграл 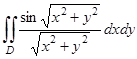 , где
, где 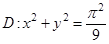 , .
, .
4) Вычислить интеграл 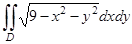 , где .
, где .
5) Отыскать площадь фигуры, ограниченной линиями:
6) Отыскать площадь фигуры, ограниченной линиями:
5.1) Вычислить 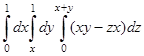 .
.
2) Вычислить 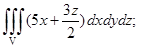 где
где
3) Вычислить 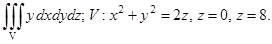
4) Вычислить количество тела , ограниченного поверхностями: , , .
5) Отыскать количество тела, заданного ограничивающими его поверхностями: .
6) Вычислить массу тела, ограниченного поверхностями и имеющего плотность .
Криволинейные интегралы
1.1)Вычислить 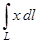 , где L – дуга параболы от т.А(2;7) до т.В(4;19);
, где L – дуга параболы от т.А(2;7) до т.В(4;19);
2) 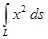 , где L – кривая ; 3)
, где L – кривая ; 3) 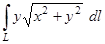 , где L —
, где L — 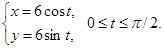
2.1) Вычислить 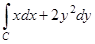 , в случае, если кривая интегрирования С: y=2×2; от А(1,2) до В(2,8).
, в случае, если кривая интегрирования С: y=2×2; от А(1,2) до В(2,8).
2) Вычислить 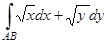 по кривой от точки до точки .
по кривой от точки до точки .
3) Вычислить 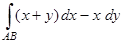 , где — ломаная, проходящая через точки , , .
, где — ломаная, проходящая через точки , , .
4) Вычислить 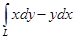 , где L – линия, заданная уравнением
, где L – линия, заданная уравнением 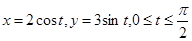 .
.
5) Вычислить 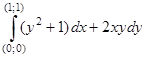 : 1) по дуге кубической параболы ; 2) по дуге . Результаты, полученные в заданиях 1 и 2 растолковать.
: 1) по дуге кубической параболы ; 2) по дуге . Результаты, полученные в заданиях 1 и 2 растолковать.
3.Вычислить криволинейные интегралы по формуле Грина:
1) 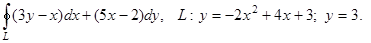
2) 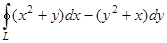 , на протяжении контура треугольника светло синий, где А(1,2), В(1,5), С(3,5).
, на протяжении контура треугольника светло синий, где А(1,2), В(1,5), С(3,5).
3) 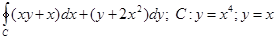 .
.
Поверхностные интегралы
1.
1) Вычислить 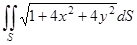 , где — часть поверхности , отсеченной плоскостью .
, где — часть поверхности , отсеченной плоскостью .
2) Вычислить 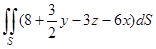 , где — часть плоскости , расположенной в четвертом октанте.
, где — часть плоскости , расположенной в четвертом октанте.
2.
1) Вычислить 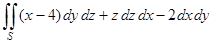 , где — верхняя сторона части плоскости, расположенной в 4ом октанте
, где — верхняя сторона части плоскости, расположенной в 4ом октанте 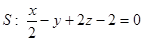 .
.
2) Вычислить 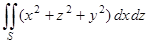 , где — внешняя сторона поверхности , отсеченная плоскостями ,
, где — внешняя сторона поверхности , отсеченная плоскостями ,
3) Вычислить 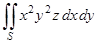 , где — верхняя сторона нижней половины сферы .
, где — верхняя сторона нижней половины сферы .
3.Вычислить интегралы, применив соответствующую теорему Остроградского-Гаусса либо Стокса
1) 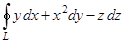 , где — окружность, заданная пересечением двух плоскости: и поверхностей цилиндра , обход по окружности производится в хорошем направлении относительно нормали к поверхности.
, где — окружность, заданная пересечением двух плоскости: и поверхностей цилиндра , обход по окружности производится в хорошем направлении относительно нормали к поверхности.
2) 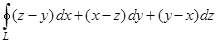 , где — контур треугольника с вершинами , , , в случае, если контур треугольника задать, как пересечение плоскости с координатными плоскостями .
, где — контур треугольника с вершинами , , , в случае, если контур треугольника задать, как пересечение плоскости с координатными плоскостями .
3) 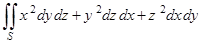 , где — верхняя сторона куба, составленного плоскостями .
, где — верхняя сторона куба, составленного плоскостями .
4) 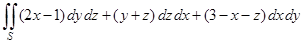 , где — поверхность цилиндра .
, где — поверхность цилиндра .
Теория поля
1. Дана точки и функция A1(-1;2;1), A2(3;1;-1)
Вычислить:
А) производную данной функции в точке A1 по направлению вектора ;
В) grad U(A1).
2. Вычислить поток векторного поля через внешнюю поверхность пирамиды, образуемую координатными плоскостями и плоскостью посредством формулы Остроградского-Гаусса.
3. Вычислить циркуляцию векторного поля по контуру треугольника, взятого в следствии пересечения плоскости с координатными плоскостями, при хорошем направлении обхода довольно обычного вектора .
4. Вычислить циркуляцию векторного поля на протяжении контура , в направлении обхода – в сторону повышения параметра t.
5. Узнать, есть ли векторное поле гармоническим.
СТРУКТУРА БИЛЕТА: 14 ТЕСТОВЫХ ЗАДАНИЯ – ПО 1 БАЛЛУ, 6 ПРАКТИЧЕСКИХ ЗАДАНИЙ – ОТ 3 ДО 6 БАЛЛОВ.
ЧТО Возможно ПРИНЕСТИ НА ЭКЗАМЕН:
Поверхности.
Вопросы
Кратные интегралы
1.1 Двойной интеграл: вычисление двойного интеграла в декартовых и в полярных координатах.
1.2 Приложения двойного интеграла к задачам геометрии.
1.3 Тройной интеграл: вычисление тройного интеграла в декартовых, цилиндрических координатах.
1.4 Приложения тройного интеграла к задачам геометрии.
Криволинейные и интегралы
2.1 Криволинейный интеграл 1-го рода: вычисление, приложения и свойства.
2.2 Криволинейный интеграл 2-го рода: свойства, вычисление, приложения. Формула Остроградского-Грина. Условия независимости криволинейного интеграла от формы пути на плоскости.
Поверхностные интегралы
3.1 Фундаментальные особенности поверхностного интеграла 1 рода, вычисление.
3.2 Определение поверхностного интеграла 2 рода.
3.3 Фундаментальные особенности поверхностного интеграла 2 рода, вычисление.
3.4 Связь между поверхностными интегралами первого и второго родов.
3.5 Формула Остроградского-Гаусса.
3.6 Формула Стокса.
Теория поля
4.1 Поле. Скалярное поле. Векторное поле.
4.2 Характеристики скалярного поля: линии (поверхности) уровня, градиент, производная по направлению.
4.3 Характеристики векторного поля: векторные линии, дивергенция, поток, циркуляция, ротор, потенциал.
Теория последовательностей
5.1 Числовой последовательность. Сходимость. Неспециализированный член последовательности. Сумма последовательности. Достаточный показатель расходимости. Обобщенно-гармонический последовательность.
5.2 Показатели сходимости: показатели Даламбера, радикальный показатель Коши, интегральный показатель Коши, показатель сравнения.
5.3 Знакочередующиеся последовательности. Безотносительная и условная сходимость. Показатель Лейбница.
5.4 Степенные последовательности: радиус и интервал сходимости. Разложение функции в степенной последовательность. Использование к приближенным вычислениям.
5.5 Последовательность Фурье. Разложение функций в ряд Фурье.
Банк задач
Последовательности
1.1) Написать первые пять участников последовательности по заданному неспециализированному участнику: а) 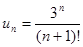 ; б)
; б) 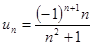 .
.
2) Отыскать суммы последовательностей: а) 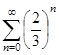 ; б)
; б) 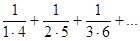 ; в)
; в) 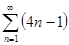 .
.
3) Изучить последовательности на сходимость: а) 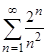 ; б)
; б) 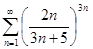 ; в)
; в) 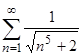 ; г)
; г) 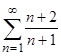 ;
;
д) 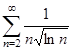 , е)
, е) 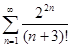 .
.
4) Изучить последовательности на безотносительную сходимость:
а) 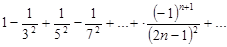 ; б)
; б) 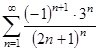 .
.
2.Отыскать область сходимости последовательностей. Узнать сходимость на финишах промежутка сходимости:а) 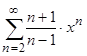 ; б)
; б) 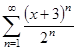 ; в)
; в) 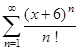 ; г)
; г) 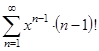 ; д)
; д) 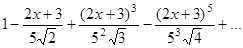
3. 1) Разложить в ряд Маклорена следующие функции (применяя «готовые» разложения):
а) ; б) ; в) ; г) ; д) 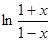 ; е)
; е) 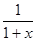 ; ж)
; ж) 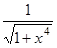 .
.
2) Вычислить приближенно с точностью до 0,001:
а) ; б) ; в) ; г) (выяснив );
ж) 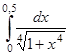 ; з)
; з) 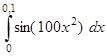 ; и)
; и) 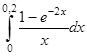 ; к)
; к) 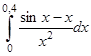 .
.
4. 1) Разложить в ряд Фурье функцию y = 1+ на (-p,p) .
2) Разложить функцию в ряд Фурье y=x-1 , -2 2.
3) Разложить функцию в ряд Фурье y=2x , -1 1.
Кратные интегралы
1.Вычислить:
1) 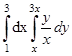 ; 2)
; 2) 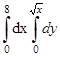 ; 3)
; 3) 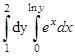 ; 4)
; 4) 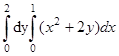 ; 5)
; 5) 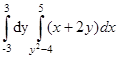 .
.
2.1) Вычислить 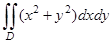 , в случае, если область ограничена линиями y = x, x = 0, y = 1, y = 2.
, в случае, если область ограничена линиями y = x, x = 0, y = 1, y = 2.
2) Вычислить 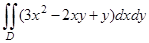 , в случае, если область ограничена линиями х = 0, х = у2, у = 2.
, в случае, если область ограничена линиями х = 0, х = у2, у = 2.
3) Вычислить 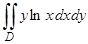 , в случае, если область интегрирования ограничена линиями ху=1, у = , х=2.
, в случае, если область интегрирования ограничена линиями ху=1, у = , х=2.
4) Вычислить 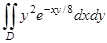 , в случае, если область интегрирования
, в случае, если область интегрирования 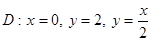 .
.
5) Вычислить 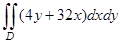 по области D, ограниченной линиями:
по области D, ограниченной линиями:
3.Отыскать площадь плоской фигуры, ограниченной линиями:
1) 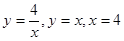 ; 2) ; 3) ;
; 2) ; 3) ;
4)
4.1) Вычислить: 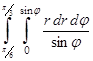 .
.
2) Вычислить 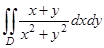 , где ограничена линиями
, где ограничена линиями
3) Вычислить интеграл 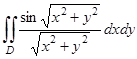 , где
, где 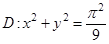 , .
, .
4) Вычислить интеграл 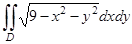 , где .
, где .
5) Отыскать площадь фигуры, ограниченной линиями:
6) Отыскать площадь фигуры, ограниченной линиями:
5.1) Вычислить 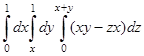 .
.
2) Вычислить 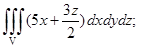 где
где
3) Вычислить 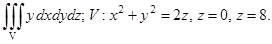
4) Вычислить количество тела , ограниченного поверхностями: , , .
5) Отыскать количество тела, заданного ограничивающими его поверхностями: .
6) Вычислить массу тела, ограниченного поверхностями и имеющего плотность .
Криволинейные интегралы
1.1)Вычислить 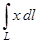 , где L – дуга параболы от т.А(2;7) до т.В(4;19);
, где L – дуга параболы от т.А(2;7) до т.В(4;19);
2) 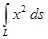 , где L – кривая ; 3)
, где L – кривая ; 3) 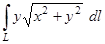 , где L —
, где L — 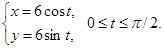
2.1) Вычислить 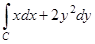 , в случае, если кривая интегрирования С: y=2×2; от А(1,2) до В(2,8).
, в случае, если кривая интегрирования С: y=2×2; от А(1,2) до В(2,8).
2) Вычислить 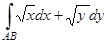 по кривой от точки до точки .
по кривой от точки до точки .
3) Вычислить 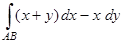 , где — ломаная, проходящая через точки , , .
, где — ломаная, проходящая через точки , , .
4) Вычислить 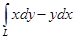 , где L – линия, заданная уравнением
, где L – линия, заданная уравнением 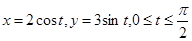 .
.
5) Вычислить 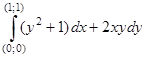 : 1) по дуге кубической параболы ; 2) по дуге . Результаты, полученные в заданиях 1 и 2 растолковать.
: 1) по дуге кубической параболы ; 2) по дуге . Результаты, полученные в заданиях 1 и 2 растолковать.
3.Вычислить криволинейные интегралы по формуле Грина:
1) 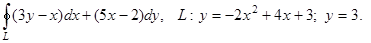
2) 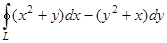 , на протяжении контура треугольника ABC, где А(1,2), В(1,5), С(3,5).
, на протяжении контура треугольника ABC, где А(1,2), В(1,5), С(3,5).
3) 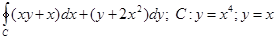 .
.
Поверхностные интегралы
1.
1) Вычислить 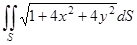 , где — часть поверхности , отсеченной плоскостью .
, где — часть поверхности , отсеченной плоскостью .
2) Вычислить 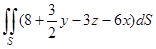 , где — часть плоскости , расположенной в четвертом октанте.
, где — часть плоскости , расположенной в четвертом октанте.
2.
1) Вычислить 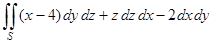 , где — верхняя сторона части плоскости, расположенной в 4ом октанте
, где — верхняя сторона части плоскости, расположенной в 4ом октанте 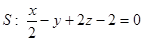 .
.
2) Вычислить 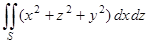 , где — внешняя сторона поверхности , отсеченная плоскостями ,
, где — внешняя сторона поверхности , отсеченная плоскостями ,
3) Вычислить 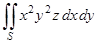 , где — верхняя сторона нижней половины сферы .
, где — верхняя сторона нижней половины сферы .
3.Вычислить интегралы, применив соответствующую теорему Остроградского-Гаусса либо Стокса
1) 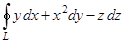 , где — окружность, заданная пересечением двух плоскости: и поверхностей цилиндра , обход по окружности производится в хорошем направлении относительно нормали к поверхности.
, где — окружность, заданная пересечением двух плоскости: и поверхностей цилиндра , обход по окружности производится в хорошем направлении относительно нормали к поверхности.
2) 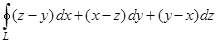 , где — контур треугольника с вершинами , , , в случае, если контур треугольника задать, как пересечение плоскости с координатными плоскостями .
, где — контур треугольника с вершинами , , , в случае, если контур треугольника задать, как пересечение плоскости с координатными плоскостями .
3) 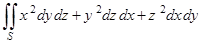 , где — верхняя сторона куба, составленного плоскостями .
, где — верхняя сторона куба, составленного плоскостями .
4) 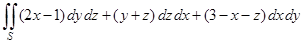 , где — поверхность цилиндра .
, где — поверхность цилиндра .
Теория поля
1. Дана точки и функция A1(-1;2;1), A2(3;1;-1)
Вычислить:
А) производную данной функции в точке A1 по направлению вектора ;
В) grad U(A1).
2. Вычислить поток векторного поля через внешнюю поверхность пирамиды, образуемую координатными плоскостями и плоскостью посредством формулы Остроградского-Гаусса.
3. Вычислить циркуляцию векторного поля по контуру треугольника, взятого в следствии пересечения плоскости с координатными плоскостями, при хорошем направлении обхода довольно обычного вектора .
4. Вычислить циркуляцию векторного поля на протяжении контура , в направлении обхода – в сторону повышения параметра t.
5. Узнать, есть ли векторное поле гармоническим.
СТРУКТУРА БИЛЕТА: 14 ТЕСТОВЫХ ЗАДАНИЯ – ПО 1 БАЛЛУ, 6 ПРАКТИЧЕСКИХ ЗАДАНИЙ – ОТ 3 ДО 6 БАЛЛОВ.
ЧТО Возможно ПРИНЕСТИ НА ЭКЗАМЕН:
Разложение функции в ряд Фурье.