Неспециализированная постановка задачи оптимизации.
Линейное программирование. Постановка задачи математического программирования начинается с определения цели(целевая функция)
F(x)=f(x)-opt(i) (max, min)
Для нахождения ответа задачи нужно выяснить переменные задачи x = (x1,x2,…,xn)ограничения накладываемые на них. Эти ограничения воображают совокупность:
g (x)
g(x)0
g(x)=0
Эти три записи составляют математическую модель задачи математического программирования.
Классификация:
В случае, если функция цели:
1. Линейная функция gi(x) кроме этого линейные функции, то модель именуется моделью лин. программирования
2. В случае, если функция цели и линейная в совокупности функций не линейные, то модель именуется моделью не линейного программирования.
3. В случае, если переменные задачи xi, являются переменные зависящими от времени, то модель именуется моделью динамического программирования.
Хорошая задача на условный экстремум. Нужные и достаточные условия условного экстремума.
Пускай функция f выяснена в некоей области G R и точкаP G. Значения функции в данной точке именуется (локальным) минимумом, соответственно, локальным максимумом функции f в G тогда и лишь тогда, в то время, когда существует некая окрестность U(P) G
Точки P такая, что для всех точек P U(P) имеет место соответственно
f(P) f(Pо). Максимум либо минимум функции f именуется кроме этого (локальным) экстремумом функции f в G. Значение локального экстремума функции f в точке Pо есть мельчайшим либо громаднейшим значением функции в некоей окрестности точки Pо, но оно не сходится, по большому счету говоря, с мельчайшим либо громаднейшим значением функции в области G.
Нужные условия существования экстремума. В случае, если f(Pо) имеется экстремум функции f, дифференцируемой по каждой из координат в некоей окрестности U(Pо) точки Pо, то имеет место f(Po)=0; (i=1,..,n)
Достаточное условие экстремума. Пускай в некоей области, содержащей Pо(хо, уо), функция f(х,у) имеет постоянные частные производные до третьего порядка включительно, пускай помимо этого, точка Pо(хо, уо) есть критической точкой функции f(х,у) т.е.
Тут ф – ла))
Способ множителей Лагранжа для ответа хорошей задачи на условный экстремум.
Способ множителей Лагранжа, способ нахождения условного экстремума функции , где , относительно ограничений , где изменяется от единицы до .
§ Составим функцию Лагранжа в виде линейной комбинации функций и функции , забранных с коэффициентами, именуемыми множителями Лагранжа — :
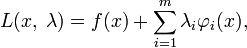
где .
§ Составим совокупность из уравнений, приравняв к нулю частные производные функции Лагранжа по и .
§ В случае, если система имеет решение относительно параметров и , тогда точка возможно условным экстремумом, другими словами ответом исходной задачи. Увидим, что это условие носит нужный, но не достаточный темперамент.
Двумерный случай
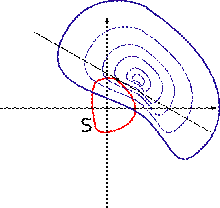
Линии уровня и кривая .
Пускай требуется отыскать экстремум некоей функции двух переменных при условии, задаваемом уравнением . Мы будем вычислять, что все функции непрерывно дифференцируемы, и данное уравнение задает ровную кривую на плоскости . Тогда задача сводится к нахождению экстремума функции на кривой . Будем кроме этого вычислять, что не проходит через точки, в которых градиент обращается в .
Нарисуем на плоскости линии уровня функции (другими словами кривые ). Из геометрических мыслей видно, что экстремумом функции на кривой смогут быть лишь точки, в которых касательные к и соответствующей линии уровня совпадают. Вправду, в случае, если кривая пересекает линию уровня в точке трансверсально (другими словами под некоторым ненулевым углом), то двигаясь по кривой из точки мы можем попасть как на линии уровня, соответствующие большему значению , так и меньшему. Следовательно, такая точка не может быть точкой экстремума.
Тем самым, нужным условием экстремума в нашем случае будет совпадение касательных. Дабы записать его в аналитической форме, увидим, что оно эквивалентно параллельности градиентов функций и в данной точке, потому, что вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:
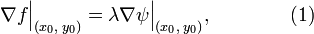
где — некое число, хорошее от нуля, и являющееся множителем Лагранжа.
Разглядим сейчас функцию Лагранжа , зависящую от и :
Нужным условием ее экстремума есть равенство нулю градиента . В соответствии с правилами дифференцирования, оно записывается в виде
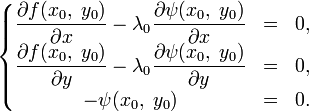
Мы взяли совокупность, первые два уравнения которой эквивалентны нужному условию локального экстремума (1), а третье — уравнению . Из нее возможно отыскать . Наряду с этим , потому, что в другом случае градиент функции обращается в нуль в точке , что противоречит отечественным версиям. Необходимо заметить, что отысканные так точки смогут и не являться искомыми точками условного экстремума — рассмотренное условие носит нужный, но не достаточный темперамент. Нахождение условного экстремума посредством запасном функции и образовывает базу способа множителей Лагранжа, примененного тут для несложного случая двух переменных. Оказывается, приведенные выше рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.
На базе способа множителей Лагранжа возможно доказать и кое-какие достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.
Противоречивость совокупности
l Очевидно, вероятен и таковой случай, в то время, когда нет ни одной точки, принадлежащей в один момент всем разглядываемым полуплоскостям, т.е. в то время, когда область К «безлюдна»; это указывает, что совокупность противоречива.
Выпуклость области ответов
l Область ответов X в любой момент выпукла.
l Множество точек (на плоскости либо в пространстве) именуется выпуклым, в случае, если вместе с любыми двумя собственными точками А и В оно содержит и целый отрезок АВ.
Постановка задачи
Хорошая транспортная задача ЛП формулируется следующим образом.
Имеется m пунктов производства (поставщиков) и n пунктов
потребления (потребителей) однородного продукта. Заданы величины:
— количество производства (запас) i-го поставщика, i=1, m ;
— количество потребления (спрос) j-го потребителя, i=1, n ;
— цена перевозки (транспортные затраты) единицы продукта от i-го поставщика к j-му потребителю.
Требуется разработать таковой замысел перевозок, при котором спрос
всех потребителей был бы выполнен и наряду с этим неспециализированная цена всех
перевозок была бы минимальна.
Математическая модель транспортной задачи имеет форму
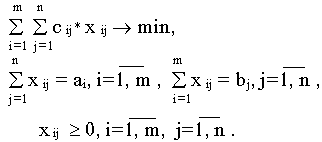
Транспортная задача, в которой суммарные запасы
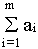
и суммарные потребности
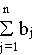
совпадают, именуется закрытой моделью; в другом случае -открытой. Открытая модель решается приведением к закрытой.
При, в то время, когда суммарные запасы превышают суммарные
потребности, т.е.
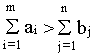
вводится фиктивный n+1 потребитель, потребности которого
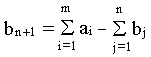
При, в то время, когда суммарные потребности превышают суммарные
запасы, т.е.
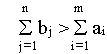
, вводится фиктивный m+1 поставщик, запасы которого
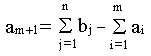
Цена перевозки единицы груза как до фиктивного потребителя, так и цена перевозки единицы груза от фиктивного поставщика
полагают равными нулю, поскольку груз и в том и другом случае не перевозится.
Перед тем как решать транспортную задачу, нужно проверить, к какой модели она в собственности, и в случае, если нужно, то привести ее к
закрытой модели.
Теорема 1.
Базовое ответ закрытой модели транспортной задачи содержит m+n-1 базовых компонент.
Подтверждение.
Количество базовых компонент определяется число линейно свободных ограничений задачи. В транспортной задаче не все m+n ограничений линейно-свободны.
Вправду, сложив первые m ограничений и следующие n ограничений задачи, возьмём
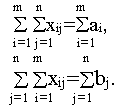
Но в закрытой модели выполняется балансовое равенство
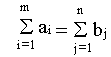
исходя из этого приобретаем, что нетривиальная линейная комбинация строчков ограничений (линейная комбинация с ненулевыми коэффициентами) равна нулю. Это указывает, что среди ограничений задачи имеется линейно-зависимое ограничение. Следовательно, число линейно-свободных ограничений равняется m+n-1 и базис задачи складывается из m+n-1 компонент.
Теорема доказана
В силу специфики содержательной постановки транспортной задачи допустимое ответ именуется замыслом, базовое допустимое ответ называетсяопорным замыслом, оптимальное ответ именуется оптимальным замыслом.
Теорема 2.
Оптимальный замысел закрытой модели транспортной задачи существует в любой момент.
Подтверждение.
Оптимальное ответ задачи ЛП существует, в случае, если, во-первых, существует допустимое ответ и, во-вторых, целевая функция ограничена на этом допустимом ответе.
Продемонстрируем существование допустимого ответа. Так как
суммарные запасы
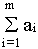
совпадают с суммарными потребностями
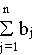
то в любой момент возможно отыскать таковой замысел перевозок, что будет допустимым ответом (все запасы вывозятся и все потребности выполняются в силу балансового равенства).
Продемонстрируем ограниченность целевой функции.
Так как
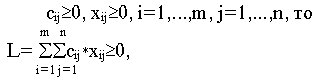
следовательно L ограничена снизу нулем для всех допустимых ответов.
Теорема доказана
Двойственная задача
Запишем транспортную задачу в матричном виде
A- матрица ограничений, имеющая в соответствии с векторами х и b вид :
Двойственная задача к транспортной задаче в матричном виде будет иметь вид
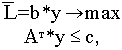
у- произвольного символа.
Распишем двойственную задачу в скалярном виде. Обозначим компоненты вектора
Тогда
и ограничения двойственной задачи будут иметь вид :
либо в общем виде двойственная задача
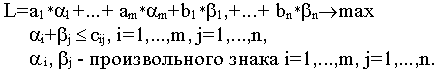
Двойственные переменные ?i, i=1,…,m, ?j, j=1,…,n, именуются платежами, а
— псевдостоимость перевозок единицы груза из пункта i в пункт j, i=1,…,m, j=1,…,n.
Теоремы двойственности
ИЗ теории двойственности ЛП практический интерес воображает вторая теорема двойственности, из которой получается следующий критерий.
Способ севево-западного угла
Разглядим северо-западный угол незаполненной таблицы, то
имеется клетку, соответствующую первому потребителю и первому поставщику.
Вероятны три случая.
Это указывает, что первый поставщик отгрузил целый произведенный продукт первому потребителю и его
запас равен нулю, исходя из этого
Наряду с этим неудовлетворенный спрос в первом пункте потребления равен
другими словами спрос первого потребителя абсолютно удовлетворен и исходя из этого
а остаток продукта в первом пункте производства равен
из рассмотрения возможно исключить и поставщика, и потребителя. Но при атом замысел получается вырожденным,
исходя из этого условно считается, что выбывает лишь поставщик,
а спрос потребителя остается неудовлетворенным и равным нулю.
Затем разглядываем северо-западный угол оставшейся не-
заполненной части таблицы и повторяем те же действия. В следствии
через n+m-1 шагов возьмём опорный замысел.
10. Математическая модель транспортной задачи. Открытые и закрытые задачи. Допустимый, опорный и оптимальный замыслы перевозок.
Называющиеся «транспортная задача» объединяется широкий круг задач с единой математической моделью. Эти задачи относятся к задачам линейного программирования и смогут быть решены симплексным способом. Но матрица совокупности ограничений транспортной задачи так необычна, что для ее решения созданы особые способы. Эти способы, как и симплексный способ, разрешают отыскать начальное опорное ответ, а после этого, улучшая его, взять оптимальное ответ.
Открытая и закрытая транспортные задачи. Выделяют два типа ТЗ: открытая ТЗ и закрытая ТЗ.
Транспортная задача именуется закрытой, в случае, если выполняется условие баланса : суммарный количество производства равен суммарному количеству потребления:
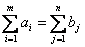. (3.1)
Следнет обратить внимание на то, что математическая модель задает закрытую транспортную задачу.
Открытая ТЗ имеет место в двух случаях.
Первый случай. Суммарный количество производства меньше суммарного количества потребления:
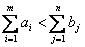. (3.2)
Как мы знаем, что для существования допустимого ответа транспортной задачи нужно и достаточно, дабы задача была закрытой. Исходя из этого транспортную задачу открытого типа предварительно нужно свести к закрытой, для чего вводится фиктивный пункт производства с номером m+1 с количеством производства:
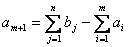, (3.3)
наряду с этим полагают .
Второй случай. Суммарный количество производства больше суммарного количества потребления:
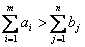. (3.4)
Для сведения ТЗ к закрытому типу вводят фиктивный пункт потребления с номером n+1 с количеством потребления:
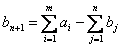, (3.5)
наряду с этим полагают .
Способы ответа.
- Как задача линейного программирования ТЗ возможно решена симплекс способом [4].
- Кроме этого созданы особые (более действенные) способы ответа транспортной задачи: обобщенный венгерский способ [4]; способ северо-западного угла, способ минимального элемента для нахождения опорного замысла; способ потенциалов для нахождения оптимального замысла [3].
11. Построение начального (опорного) замысла перевозок по способу северо–западного угла и по способу мельчайшей цене.
1.Способ северо-западного угла. При нахождении опорного замысла на каждом шаге разглядывают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для малоизвестного («северо-западный угол») и заканчивается клеткой для малоизвестного , т.е. как бы по диагонали таблицы.
2. Способ мельчайшей цене. Сущность способа содержится в том, что из всей таблицы цен выбирают мельчайшую и в клетку , которая ей соответствует, помещают меньшее из чисел и , после этого из рассмотрения исключают или строчок, соответствующую поставщику, запасы которого абсолютно израсходованы, или столбец, соответствующий потребителю, потребности которого абсолютно удовлетворены, или и столбец и строку, в случае, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы цен опять выбирают мельчайшую цена, и процесс размещения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Формула полной возможности.
Пускай событие A может случиться лишь вместе с одним из попарно несовместных событий H1, H2, …, Hn, образующих полную группу. Тогда, в случае, если случилось событие A, то это значит, что случилось одно из попарно несовместных событий H1A, H2A, …, HnA. Следовательно,
Используя теорему сложения возможностей, имеем
Но (i=1, 2, …, n), исходя из этого
Эта формула именуется формулой полной возможности. События H1, H2, …, Hn довольно часто именуют «догадками».
Теорема Байеса.
Теорема Байеса— разрешает выяснить возможность того, что случилось какое-либо событие (догадка) при наличии только косвенных тому подтверждений (данных), каковые смогут быть неточны.
Формула Байеса:
,
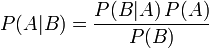где
— априорная возможность (как возможна обстоятельство по большому счету) догадки A
— возможность догадки A при наступлении события B
— возможность наступления события B при истинности догадки A
— полная возможность наступления события B.
Следствие
Формула Байеса есть ответственным следствием из формулы полной возможности события, зависящего от нескольких несовместных догадок (и лишь от них!).
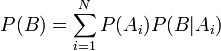— возможность наступления события B, зависящего от последовательности догадок , в случае, если известны степени достоверности этих догадок (к примеру, измерены экспериментально);
Формула Бернулли
В случае, если производятся опробования, при которых возможность появления события А в каждом опробовании не зависит от финалов вторых опробований, то такие опробования именуют свободными относительно события А.
Возможность того, что в n свободных опробованиях, в каждом из которых возможность появления события равна р(0 p 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна:
Pn(k)=Cnkpkqn-k
либо
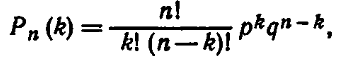
где q=1-p
Возможность того, что в n опробованиях событие наступит: а) менее k раз; б) более k раз; в) не меньше k раз; г) не более k раз, — находят соответственно по формулам:
Pn(0)+Pn(1)+…+Pn(k-1);
Pn(k+1)+Pn(k+2)+…+Pn(n);
Pn(0)+Pn(1)+…+Pn(k);
Правило трех сигм
Правила трех сигм: в случае, если случайная величина распределена нормально, то безотносительная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
P(|X ? a| ?) = 2? ?)
положив ? = ?t. В итоге возьмём
P(|X ? a| ?t) = 2? (t).
В случае, если t = 3 и, следовательно, ?t = 3?, то
P(|X ? a| 3?) = 2? (3) = 2 · 0.49865 = 0.9973,
На практике правило трех сигм используют так: в случае, если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, другими словами основание предполагать, что изучаемая величина распределена нормально; в другом случае она не распределена нормально.
37) Понятие о теореме Ляпунова
Теорема Ляпунова — теорема в теории возможностей, устанавливающая кое-какие неспециализированные достаточные условия для сходимости распределения сумм свободных случайных размеров к обычному закону.
в случае, если случайная величина является суммой большого числа взаимно свободных случайных размеров, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к обычному.
Довольно часто приходится иметь дело с этими случайными размерами, каковые являются суммами солидного числа свободных случайных размеров. При некоторых очень неспециализированных условиях выясняется, что эта сумма имеет распределение, близкое к обычному, не смотря на то, что каждое из слагаемых может не подчиняться обычному закону распределения возможностей. Эти условия были отысканы Ляпуновым и составляют содержание теоремы, названной его именем.
Пускай с последовательность попарно свободных случайных размеров с математическими ожиданиями M и дисперсиями D , причём эти размеры владеют следующими двумя особенностями:
1) Существует такое число L, что для любого i имеет место неравенство т, е. все значения случайных размеров, как говорят, равномерно ограничены, довольно математических ожиданий;
2) Сумма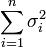 
неограниченно растёт при .
Тогда при большом n сумма имеет распределение, близкое к обычному.
Пускай и дисперсия и математическое ожидание случайной величины Тогда:
.
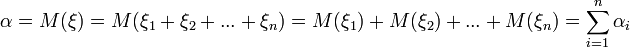
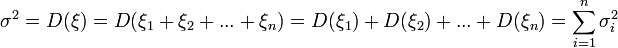
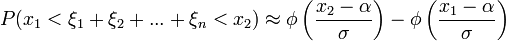Ц.П.Т. Ляпунова
Пускай выполнены базисные догадки Ц.П.Т. Линдеберга. Пускай случайные размеры имеют конечный третий момент. Тогда выяснена последовательность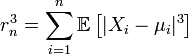 
В случае, если предел 
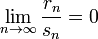(условие Ляпунова), то
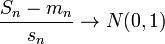по распределению при .
38)Закон солидных чисел.
Зако?н больши?х чи?сел в теории возможностей говорит, что эмпирическое среднее (среднее арифметическое) большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают не сильный закон солидных чисел, в то время, когда имеет место сходимость по возможности, и усиленный закон солидных чисел, в то время, когда имеет место сходимость практически везде.
В любой момент найдётся такое количество опробований, при котором с любой заданной наперёд возможностью относительная частота появления некоего события будет сколь угодно слабо отличается от его возможности.
Неспециализированный суть закона солидных чисел — совместное воздействие солидного числа случайных факторов ведет к результату, практически не зависящему от случая.
На этом свойстве основаны способы оценки возможности на базе анализа конечной выборки. Наглядным примером есть прогноз результатов выборов на базе опроса выборки избирателей.
не сильный закон солидных чисел
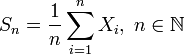
Тогда, .
Неравенство Чебышева
p( | X – M(X)| ? ) ? D(X) / ??.
Подтверждение. Пускай Х задается рядом распределения
| Х | направляться1 | х2 | … | хп |
| р | р1 | р2 | … | рп |
Так как события |X – M(X)| ? и |X – M(X)| ? ? противоположны, то р ( |X – M(X)| ? ) + + р ( |X – M(X)| ? ? ) = 1, следовательно, р ( |X – M(X)| ? ) = 1 — р ( |X – M(X)| ? ? ). Отыщем р ( |X – M(X)| ? ? ).
D(X) = (x1 – M(X))?p1 + (x2 – M(X))?p2 + … + (xn – M(X))?pn . Исключим из данной суммы те слагаемые, для которых |X – M(X)| ?. Наряду с этим сумма может лишь уменьшиться, поскольку все входящие в нее слагаемые неотрицательны. Для определенности будем вычислять, что отброшены первые kслагаемых. Тогда
D(X) ? (xk+1 – M(X))?pk+1 + (xk+2 – M(X))?pk+2 + … + (xn – M(X))?pn ? ?? (pk+1 + pk+2 + … + pn).
Напомним, что pk+1 + pk+2 + … + pn имеется возможность того, что |X – M(X)| ? ?, так как это сумма возможностей всех вероятных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ? ?? р(|X – M(X)| ? ?), либо р (|X – M(X)| ? ?) ? D(X) / ??. Тогда возможность противоположного события p( | X – M(X)| ? ) ? D(X) / ??, что и требовалось доказать
Теорема Чебышева:
Распределение Стьюдента
Пускай случайная величина x имеет стандартное обычное распределение, а случайная величина c n2 — c 2-распределение с n степенями свободы.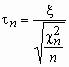 
В случае, если x и c n2 — свободны, то про случайную величину говорят, что она имеет распределение Стьюдента с n степенями свободы. Плотность возможности данной случайной величины вычисляется по формуле:
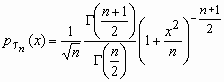, x R,Mt n = 0,Dt n = n/(n-2), n2.
При громадных n распределение Стьюдента фактически не отличается от N(0, 1).
Распределение Фишера
Пускай случайные размеры c n2и c m2 свободны и имеют распределение c 2 с n и m степенями свободы соответственно.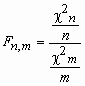 
Тогда о случайной величине говорят, что она имеет F-распределение. Плотность возможности данной случайной величины вычисляется по формуле:
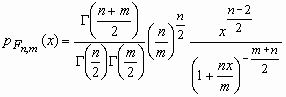, x0,
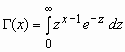— гамма-функция Эйлера;
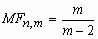, m2;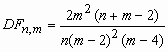 
, m 4.
53. Критерии и правила проверки догадок: о равенстве математических ожиданий и дисперсий двух обычных главных совокупностей; о том, что главная совокупность распределена по обычному закону.
Неспециализированная постановка задачи оптимизации.
Линейное программирование. Постановка задачи математического программирования начинается с определения цели(целевая функция)
F(x)=f(x)-opt(i) (max, min)
Для нахождения ответа задачи нужно выяснить переменные задачи x = (x1,x2,…,xn)ограничения накладываемые на них. Эти ограничения воображают совокупность:
g (x)
g(x)0
g(x)=0
Эти три записи составляют математическую модель задачи математического программирования.
Классификация:
В случае, если функция цели:
1. Линейная функция gi(x) кроме этого линейные функции, то модель именуется моделью лин. программирования
2. В случае, если функция цели и линейная в совокупности функций не линейные, то модель именуется моделью не линейного программирования.
3. В случае, если переменные задачи xi, являются переменные зависящими от времени, то модель именуется моделью динамического программирования.