Физическая химия
Разделы физической химии
Физическая химия -наука, изучающая химические явления и устанавливающая их неспециализированные закономерности на базе физических подходов и с применением физических экспериментальных способов.
Разделы физической химии :
- Строение вещества
- термохимия и Химическая термодинамика
- Химическое и фазовое равновесие
- электрохимия и Растворы
- Химическая кинетика. Катализ. Фотохимия
- Радиационная химия
величины и Основные понятия
ТемператураТ — степень нагретости тела, определяемая распределением других частиц и молекул по скоростям кинетического перемещения и степенью заселённости наибольших энергетических уровней молекул. В термодинамике принято применять полную температуру, отсчитываемую от безотносительного нуля, которая в любой момент хороша. Размерность СИ безотносительной температуры – К (кельвин), численно равный градусу шкалы Цельсия.
Работа- форма энергопередачи от одной совокупности к второй, которая связана с действием против внешних сил и осуществляемая при упорядоченном, направленном перемещении совокупности либо отдельных её составных частей. Количественной мерой энергии, передаваемой при работе, помогает количество работы w. Размерность СИ работы — Дж. Вместо термина “количество работы” довольно часто как синоним употребляется выражение “работа”.
количество теплоты и Количество работы в общем случае не являются функциями состояния, поскольку их значение определяется видом процесса, из-за которого совокупность поменяла собственный состояние. Исключениями являются тепловой эффект и работа расширения химической реакции.
Сам термин “термодинамика” происходит от греческих слов thermos (теплота) и dynamos (работа), так как эта наука основана на изучении работы и баланса теплоты в совокупностях при разных процессах.
ТеплоёмкостьС — отношение количества теплоты, поглощаемой телом при нагревании, к трансформации температуры, вызываемому этим поглощением. Различают истиннуюи среднюю, молярную и удельную, изобарную и изохорную теплоёмкость.
Подлинная теплоёмкость — отношение бесконечно малого количества теплоты к вечно малому трансформации температуры:
Сист= dQ/dT
средняя теплоёмкость- отношение макроскопического количества теплоты к трансформации температуры в макроскопическом ходе:
С= DQ/DT .
По физическому смыслу средняя теплоёмкость является количеством теплоты, нужное для нагревания тела на 1 градус (1оС либо 1К).
Теплоёмкость единицы массы вещества — удельная теплоёмкость(размерность кг — и/СИ·К). Теплоёмкость моля вещества — молярная(мольная)теплоёмкость(размерность СИ — Дж/моль·К). Теплоёмкость, измеренная при постоянном количестве — изохорная теплоёмкостьСV; теплоёмкость при постоянном давлении — изобарная теплоёмкостьСP. Между СP и СV существует соотношение (для одного моля совершенного газа):
СP = СV + R
где R — универсальная газовая постоянная.
Термодинамические совокупности
Термодинамическая совокупность- конкретный объект термодинамического изучения, в мыслях обособляемый от экологии. Это совокупность макроскопических тел, каковые смогут взаимодействовать между собой и с внешней средой — обмениваться с ними веществом и энергией. Термодинамическая совокупность складывается из столь солидного числа структурных частиц, что её состояние возможно характеризовать макроскопическими параметрами: плотностью, давлением ,концентрацией веществ, температурой и др.
Термодинамические совокупности (либо, для краткости, легко совокупности) смогут быть классифицированыпо разным показателям:
— по состоянию: равновесные и неравновесные;
— по сотрудничеству с окружающей средой (либо с другими совокупностями): открытые (смогут обмениваться со энергией и средой, и веществом), закрытые (смогут обмениваться лишь энергией) и изолированные (не смогут обмениваться ни веществом, ни энергией);
— по числу фаз: семь дней (гомогенные, однородные) и многофазные (неоднородные, неоднородные);
— по числу компонентов (веществ, входящих в их состав): однокомпонентные и многокомпонентные.
Внутренняя энергиярассматриваемой совокупности U — сумма всех взаимодействия энергии частиц и видов движения (молекул, атомов, ионов, радикалов и др.), складывающих совокупность — кинетической энергии хаотического перемещения молекул относительно центра масс системы и потенциальной энергии сотрудничества молекул между собой. Составляющие внутренней энергии — поступательная Uпост (энергия поступательного перемещения частиц, к примеру молекул газов и жидкостей), вращательная Uвр (энергия вращательного перемещения частиц, к примеру, вращения молекул газов и жидкостей, атомов около химических s-связей), колебательная Uкол (энергия внутримолекулярного колебательного перемещения атомов и энергия колебательного перемещения частиц, находящихся в узлах кристаллической решётки), электронная Uэл (энергия перемещения электронов в молекулах и атомах), ядерная энергия Uя и др. В понятие внутренней энергии не входят кинетическая и потенциальная энергия совокупности в целом. Размерность СИ внутренней энергии Дж/моль либо Дж/кг.
Безотносительное значение внутренней энергии не может быть вычислено посредством уравнений термодинамики. Возможно только измерить её изменение в том либо другом ходе. Но для термодинамического рассмотрения это оказывается достаточным.
Параметры состояния
Состояниесистемы — совокупность физических и химических особенностей, характеризующих данную совокупность. Оно описывается параметрамисостояния — температурой Т, давлением р, количеством V, концентрацией С и др. Каждому состоянию совокупности не считая определённого значения параметров отвечает кроме этого определённое значение некоторых размеров, зависящих от параметров и именуемых термодинамическими функциями. В случае, если изменение термодинамической функции не зависит от пути процесса, а определяется лишь начальным и конечным состоянием, такая функция именуется функцией состояния. К примеру, внутренняя энергия есть функцией состояния, потому, что её изменение в каком-либо ходе возможно вычислено как разность между конечным и начальным значениями:
DU = U2 — U1 .
К функциям состояния относятся характеристические функции, совокупность которых может достаточно полно охарактеризовать состояние совокупности (внутренняя энергия, энтальпия, энтропия, энергия Гиббса и т. п.).
Термодинамический процесс- это любое изменение в совокупности, сопровождающееся трансформацией параметров. Движущей силой процессов являются факторы- неравномерность значения тех либо иных параметров (к примеру, температурный фактор, обусловленный разными значениями температуры в различных частях совокупности). Процесс, идущий при постоянном давлении, именуется изобарным, при постоянном количестве — изохорным, при постоянной температуре — изотермическим, при постоянном количестве теплоты — адиабатическим.
Теплота- форма хаотичного (“теплового”) перемещения образующих тело частиц (молекул, атомов и др.). Количественной мерой энергии, передаваемой при теплообмене, помогает количество теплоты Q. Размерность СИ количества теплоты — Дж. Наровне с джоулем довольно часто употребляется и внесистемная единица теплоты — калория (кал). 1 кал = 4,184 Дж. Довольно часто вместо термина “количество теплоты” в качестве синонима употребляется выражение “теплота”.
Работа- форма энергопередачи от одной совокупности к второй, которая связана с действием против внешних сил и осуществляемая при упорядоченном, направленном перемещении совокупности либо отдельных её составных частей. Количественной мерой энергии, передаваемой при работе, помогает количество работы w. Размерность СИ работы — Дж. Вместо термина “количество работы” довольно часто как синоним употребляется выражение “работа”.
Термохимия.
Термохимия- раздел химической термодинамики, занимающийся определением тепловых эффектов химических реакций и установлением их зависимости от разных условий. В задачу термохимии входит кроме этого измерение теплоёмкостей веществ и теплот фазовых переходов (а также разбавления растворов и процессов образования).
Калориметрические измерения
Главным экспериментальным способом термохимии есть калориметрия. Количество теплоты, выделяемой либо поглощаемой в химической реакции, измеряется посредством прибора, именуемого калориметром.
Калориметрические измерения разрешают рассчитывать очень ответственные размеры — тепловые эффекты химических реакций, теплоты растворения, энергии химических связей. Значения энергий связи обусловливают реакционную свойство химических соединений, а во многих случаях и фармакологическую активность лекарственных веществ. Но калориметрическим измерениям поддаются не все химические реакции и физико-химические процессы, а лишь те, каковые удовлетворяют двум условиям: 1) процесс должен быть необратимым и 2) процесс обязан протекать достаточно скоро, дабы выделяющаяся теплота не успевала рассеяться в окружающей среде.
Энтальпия
Большая часть химических процессов, как в природе, так и в лаборатории, и в индустрии протекает не при постоянном количестве, а при постоянном давлении. Наряду с этим довольно часто из разных видов работы совершается лишь один — работа расширения, равная произведению давления на трансформацию количества совокупности:
w = рDV.
При таких условиях уравнение первого начала термодинамики возможно записать в виде
DU = Qр — рDV
либо
Qр = DU + рDV
(индекс Р говорит о том, что количество теплоты измеряется при постоянном давлении). Заменяя трансформации размеров на соответствующие разности, приобретаем:
Qp = U2 — U1 + p (V2 — V1)
откуда
Qp = (U2 + pV2) — (U1 + pV1)
либо
Qp = (U + pV) 2 — (U + pV) 1 = H2 — H1
Так как p и V — параметры состояния, а U — функция состояния, то сумма U + рV = Н также есть функцией состояния. Эта функция именуется энтaльпией. Так, теплота, поглощаемая либо выделяемая совокупностью в ходе, идущем при постоянном давлении, равна трансформации энтальпии:
Qp = DH.
Между изменением и изменением энтальпии внутренней энергии совокупности существует связь, высказываемая уравнениями
DН = DU + DnRT либо DU = DН — DnRT,
каковые возможно взять с применением уравнения Менделеева — Клапейрона
pV = nRT , откуда pDV = DnRT.
Величины DН разных процессов довольно легко измеряются посредством калориметрических установок, действующий при постоянном давлении. Благодаря этого изменение энтальпии находит широкое использование при термодинамических и термохимических изучениях. Размерность СИ энтальпии — Дж/моль.
Закон Гесса
В 1840-х г.г. Г.И.Гесс сформулировал основной закон термохимии, названный им законом постоянства сумм тепла:
В то время, когда образуется какое-либо химическое соединение, то наряду с этим постоянно выделяется одно да и то же количество тепла независимо от того, происходит ли образование этого соединения конкретно либо же косвенным путём и в пара приёмов.
В современных трактовках закон звучит так:
1. В случае, если из данных исходных веществ возможно взять заданные конечные продукты различными дорогами, то суммарная теплота процесса на одном каком-либо пути равна суммарной теплоте процесса на любом втором пути.
2. Тепловой эффект химической реакции не зависит от пути процесса, а зависит лишь от свойств и вида исходных веществ и продуктов.
3. Тепловой эффект последовательности последовательных реакций равен тепловому эффекту любого другого последовательности реакций с теми же конечными продуктами и исходными веществами.
4. К примеру, водный раствор хлорида аммония (NH4Cl·aq) возможно взят из газообразных аммиака и хлороводорода и жидкой воды (aq) следующими двумя дорогами:
5. I. 1) NH3(г) + aq = NH3·aq + DH1 (DH1 = -34,936 кДж/моль);
6. 2) HCl(г) + aq = HCl·aq + DH2 (DH2 = -72,457 кДж/моль);
7. 3) NH3·aq + HCl·aq = NH4Cl·aq + DH3 (DH3 = -51,338 кДж/моль);
8. DH = DH1 + DH2 + DH3 = -34,936 -72,457 -51,338 =
9. = -158, 749 кДж/моль
10.
11. II. 1) NH3(г) + HCl(г) = NH4Cl(т) + DH4 (DH4 = -175,100 кДж/моль);
12. 2) NH4Cl(т) + aq = NH4Cl·aq + DH5 (DH5 = + 16,393 кДж/моль);
13. DH = DH4 + DH5 = -175,100 + 16,393 = -158,707
Как видно, тепловой эффект процесса, совершённого по пути I, равен тепловому эффекту процесса, совершённого но пути II (разность в 0,42 кДж/моль, составляющая 0,026 % от безотносительного значения, в полной мере укладывается в погрешность опыта).
Еще один пример. Сгорание графита до СО2 возможно осуществить двумя дорогами:
I. С(т) + О2 (г) = СО2 (г) + DН1 (DН1 = -393,505 кДж/моль);
II. C(T) + 1/2 O2 (г) = CO(г) + DH2 (DH2 = -110,541 кДж/моль);
CO(г) + 1/2 O2 (г) = СО2 (г) + DН3 (DН3 = -282,964 кДж/моль);
И в этом случае
DH = DH2 + DH3 = -110,541 + (-282,964) = -393,505 кДж/моль.
Закон Гесса разрешает вычислять тепловые эффекты многих реакций посредством довольно маленького количества справочных данных по теплотам образования и сгорания веществ, а помимо этого — рассчитывать тепловые эффекты и таких реакций, каковые по большому счету не поддаются прямому калориметрированию, к примеру, С(т) + 1/2 O2 (г) = СО(г)). Это достигается применением следствий закона Гесса.
1 следствие (закон Лавуазье — Лапласа): Тепловой эффект разложения сложного вещества на более простые численно равен, но противоположен по символу тепловому эффекту образования данного сложного вещества из данных более несложных.
К примеру, теплота разложения карбоната кальция (кальцита) на углекислый газ и оксид кальция
CaСО3 (T) = СO2 (г) + CaO(т) + DН1
равна + 178,23 кДж/моль. Значит для образования одного моля СаСО3 из СаО и СО2 выделится то же количество энергии:
CaO (T) + CО2 (T) = CaСО3 (T) + DH2 (DH2 = -178,23 кДж/моль).
2 следствие: В случае, если совершаются две реакции, приводящие из разных начальных состояний к однообразным конечным, то разность между их тепловыми эффектами равна тепловому эффекту реакции перехода от одного начального состояния к второму начальному.
К примеру, в случае, если известны тепловые эффекты графита сгорания и реакций алмаза:
С(гр) + О2 = CO2 — 393,51 кДж/моль
С(алм) + О2 = CO2 — 395,39 кДж/моль
возможно вычислить тепловой эффект перехода из одного аллотропного метаморфозы в второе:
С(гр) ® С(алм) + DHаллотропн
DHаллотропн = -393,51 — (-395,39 ) = +1,88 кДж/моль
3 следствие: В случае, если совершаются две реакции, приводящие из однообразных начальных состояний к разным конечным, то разность между их тепловыми эффектами равна тепловому эффекту реакции перехода из одного конечного состояния к второму конечному.
К примеру, пользуясь этим следствием возможно вычислить тепловой эффект реакции сгорания углерода до СО:
С(гр) + О2 ® CO2 — 393,505 кДж/моль
CO + 1/2 O2 ® CO2 — 282,964 кДж/моль
С(гр) + 1/2 O2 ® CO + DHr
DHr = -393,505 — (-282,964 ) = -110,541 кДж/моль.
4 следствие: Тепловой эффект любой химической реакции равен разности между суммами теплот образования продуктов исходных веществ и реакции (с учётом стехиометрических коэффициентов в уравнении реакции):
DHr = a(niDHf i) прод — a(niDHf i) исх
К примеру, тепловой эффект реакции этерификации
СН3СООН(ж) + С2Н5ОН(ж) = СН3СООС2Н5(ж) + Н2О(ж) + DHr
равен:
DHr = (DHf СН3СООС2Н5 +DHf Н2О) — (DHf СН3СООН +DHf С2Н5ОН) =
= (-479,03 -285,83) — (-484,09 -276,98) = -3,79 кДж..
5 следствие: Тепловой эффект любой химической реакции равен разности между суммами теплот сгорания исходных веществ и продуктов реакции (с учётом стехиометрических коэффициентов в уравнении реакции):
DHr = a(niDHc i) исх — a(niDHc i) прод
К примеру, тепловой эффект реакции этерификации, приведённой в прошлом примере,
равен:
DHr = (DHс СН3СООН +DHс С2Н5ОН) — (DHс СН3СООС2Н5 +DHс Н2О)=
= (-874,58 -1370,68) — (-2246,39 -0) = -1,13 кДж.
(Расхождение результатов разъясняется разной точностью приводимых в справочниках термохимических данных).
Теплота растворения
Теплота растворения DНр-р либо DНs.(от solution — раствор) — тепловой эффект растворения вещества при постоянном давлении.
Различают интегральную и дифференциальную теплоту растворения. Теплота растворения 1 моля вещества с образованием т. н. вечно разбавленного раствора именуется интегральной теплотой растворения. Интегральная теплота растворения зависит от соотношения количеств растворяемого растворителя и вещества и, следовательно, от концентрации образующегося раствора. Тепловой эффект при растворении 1 моля вещества крайне много уже имеющегося раствора этого же вещества некоей концентрации (приводящем к вечно малому повышению концентрации) именуется дифференциальной теплотой растворения:
| d(DНр-р) DНр-р дифф = ¾¾¾¾ . dT |
По физическому смыслу дифференциальная теплота растворения показывает, как изменяется тепловой эффект растворения вещества с повышением его концентрации в растворе. Размерность СИ теплоты растворения — Дж/моль.
Интегральная теплота растворения кристаллических веществ (к примеру, неорганических солей, оснований и т. п.) складывается из двух размеров — энтальпии превращения кристаллической решётки вещества в ионный газ (разрушения кристаллической решетки)DНреш и энтальпии сольватации (при водных растворов — гидратации)молекул и образующихся из них при диссоциации ионов DНсольв (DНгидр):
DНр-р = DНреш + DНсольв; DНр-р = DНреш + DНгидр
Величины DНреш и DНсольв противоположны по символу (гидратация и сольватация постоянно сопровождаются выделением теплоты, в то время как разрушение кристаллической решётки — её поглощением). Так, растворение веществ, владеющих не весьма прочной кристаллической решёткой (к примеру, гидроксидов щелочных металлов – NaOH, КОН и т. п.), сопровождается сильным разогреванием образующегося раствора, а отлично гидратирующихся жидких веществ, не имеющих кристаллической решётки (к примеру, серной кислоты) — ещё бoльшим разогреванием впредь до вскипания. Наоборот, растворение веществ с прочной кристаллической решёткой, таких, как, к примеру, галогениды щелочных и щёлочноземельных металлов KCl, NaCl, CaCl2, идёт с поглощением теплоты и ведет к охлаждению. (Данный эффект употребляется в лабораторной практике для изготовление охлаждающих смесей).
Исходя из этого символ суммарного теплового результата при растворении зависит от того, какое из его слагаемых больше по безотносительной величине.
В случае, если известна энтальпия разрушения кристаллической решетки соли, то, измеряя теплоту растворения, возможно вычислять энтальпию её сольватации. Иначе, измеряя теплоту растворения кристаллогидрата (т. е. гидратированной соли), возможно с достаточной точностью вычислить энтальпию разрушения (прочность) кристаллической решётки.
Теплота растворения хлорида калия, равная +17,577 кДж/моль при концентрации 0,278 моль/л и 25оС, предложена в качестве термохимического стандарта для проверки работы калориметров.
Температурная зависимость теплот растворения, как и тепловых эффектов химических реакций, подчиняется уравнению Кирхгоффа.
В то время, когда растворяемое растворитель и вещество химически подобны и при растворении не появляется осложнений, которые связаны с ионизацией либо сольватацией, теплоту растворения можно считать примерно равной теплоте плавления растворяемого вещества. По большей части это относится к растворению органических веществ в неполярных растворителях.
Энтропия
Энтропия-мера беспорядка совокупности, которая связана с термодинамической возможностью.
Рассеяние энергии среди компонентов совокупности возможно вычислено способами статистической термодинамики. Это ведет к статистическому определению энтропии. В соответствии с ранееупомянутому положению о том, что направление самопроизвольного трансформации соответствует направлению повышения термодинамической возможности, возможно заключить, что рассеяние энергии, соответственно, и энтропия связаны с ней. Эту сообщение доказал в 1872 г. Л.Больцман. Она выражается уравнением Больцмана
S = k lnW , (3.1)
где k — константа Больцмана.
В соответствии с статистической мнению, энтропия есть мерой беспорядка в совокупности. Это связано с тем, что чем больше в совокупности участков, в которых имеется пространственное упорядочение в размещении частиц либо неравномерное распределение энергии (которое также считается упорядочением энергии), тем меньше термодинамическая возможность. При хаотическом перемешивании частиц, и при равномерном распределении энергии, в то время, когда частицы нельзя различить по их энергетическому состоянию, термодинамическая возможность, а, следовательно, и энтропия, возрастают.
Второе начало термодинамики
второе возможно выражено несколькими разными формулировками, любая из которых дополняет другие:
1. Теплота не имеет возможности самопроизвольно передаваться от более холодного тела к более тёплому.
2. Энергия разных видов пытается перейти в теплоту, а теплота пытается рассеяться.
3. Никакая совокупность процессов не имеет возможности сводиться к передаче теплоты от холодного тела к тёплому, в то время как передача теплоты от тёплого тела к холодному возможно единственным результатом процессов (Р.Э.Клаузиус).
4. Никакая совокупность процессов не имеет возможности сводиться лишь к превращению теплоты в работу, в то время как превращение работы в теплоту возможно единственным результатом процессов (У.Томсон).
5. Нереально выстроить циклически трудящуюся машину, которая превращала бы теплоту в работу, не создавая наряду с этим никаких вторых трансформаций в окружающих телах (т. н. вечный двигатель второго рода) (В.Оствальд).
Для необратимого цикла Карно возможно записать:
| Q1 — Q2T1 — T2 ¾¾¾¾ = ¾¾¾¾ = h Q1T1 |
где Q1 — начальный запас теплоты в совокупности, Q2 – количество теплоты, оставшееся в совокупности по окончании прохождения в ней какого-либо процесса, T1 и T2 — соответственно начальная и конечная температура совокупности, h — коэффициент нужного действия процесса.
Это равенство есть математическим выражением второго начала термодинамики.
Третье начало термодинамики. Постулат Планка.
Безотносительная энтропия
Потому, что энтропия — величина экстенсивная, её значение для вещества при каждой данной температуре Т есть суммой значений, соответствующих каждой температуре в промежутке от 0 К до Т. В случае, если в уравнении (3.5) принять нижнюю температуру промежутка интегрирования равной безотносительному нулю, то
| 2 Т2 dT o dS = Cp o ¾¾ . 1 0 T |
Следовательно, зная значение энтропии при безотносительном нуле, посредством этого уравнения возможно было бы взять значение энтропии при любой температуре.
Тщательные измерения, совершённые в конце XIX века, продемонстрировали, что при приближении температуры к безотносительному нулю теплоёмкость любых веществ Ср пытается к нулю:
lim Cp = 0 .
T ® 0
Это значит, что величина Ср/Т конечна либо равна нулю и, следовательно, разность ST — S0 в любой момент хороша либо равна нулю. На основании этих рассуждений М.Планк(1912) внес предложение постулат:
При безотносительном нуле температуры энтропия любого вещества в виде совершенного кристалла равна нулю.
Данный постулат Планка есть одной из формулировок 3 начала термодинамики. Его возможно пояснить на базе представлений статистической физики: для идеально упорядоченного кристалла при безотносительном нуле температуры, в то время, когда тепловое перемещение частиц отсутствует, термодинамическая возможность W равна 1. Значит, в соответствии с уравнением Больцмана(3.1), его энтропия равна нулю:
ЖД0 = k ln 1 = 0
Из постулата Планка возможно сделать вывод о том, что энтропия любого вещества при температурах, отличающихся от полного нуля, есть конечной и хорошей. В соответствии с этим энтропия есть единственной термодинамической функцией состояния, для которой возможно выяснить полное значение, а не только изменение в каком-либо ходе, как при вторых функций состояния (к примеру, энтальпии и внутренней энергии).
Из вышеприведённых уравнений направляться кроме этого, что при температуре, приближающейся к полному нулю, от охлаждаемого тела делается неосуществимым забрать какие-либо, кроме того малые, количества теплоты из-за вечно малой теплоёмкости. Иными словами,
посредством конечного числа операций нереально понизить температуру тела до безотносительного нуля.
Это выражение носит название принципа недостижимости безотносительного нуля температуры и наровне с постулатом Планка есть одной из формулировок третьего начала термодинамики. (Напомним, что на данный момент в опыте удалось понизить температуру до 0,00001 К).
Принцип недостижимости безотносительного нуля температуры связан и с тепловой теоремой В.Нернста(1906), в соответствии с которой при приближении к полному нулю величины DН и DG = DН + ТDS (G — энергия Гиббса, о которой будет говориться ниже) сближаются, другими словами при Т = 0 должно иметь место равенство
DG = DН.
Изменение энтропии на протяжении химической реакции DSоr возможно вычислить как разность между суммами энтропий продуктов и исходных веществ, забранных с соответствующими стехиометрическими коэффициентами. Для стандартных условий:
DSоr = a( ni Soi) прод — a (ni So I) исх
(Для расчётов берутся безотносительные значения энтропии личных веществ, а не их трансформации, как при вычислении вторых термодинамических функций. Обстоятельства этого будут растолкованы при рассмотрении третьего начала термодинамики).
Химическое равновесие
Химическое равновесие– это термодинамическое равновесие в совокупности, в которой вероятны прямые и обратные химические реакции.
При определенных условиях активности реагентов смогут быть заменены концентрациями либо парциальными давлениями. В этих обстоятельствах константа равновесия, выраженная через равновесные концентрации Kc либо через парциальные давления Kp, принимает вид
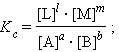
|
(4.11) |
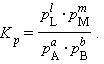
|
(4.12) |
Уравнения (4.11) и (4.12) представляют собой варианты закона действующих весов (ЗДМ) для обратимых реакций в состоянии равновесия. При постоянной температуре отношение равновесных концентраций (парциальных давлений) конечных продуктов к равновесным концентрациям (парциальным давлениям) исходных реагентов, возведенных соответственно в степени, равные их стехиометрическим коэффициентам, величина постоянная .
Для газообразных веществ Kp и Kc связаны соотношением Kp = (RT)?nKc, где ?n – разность числа молей начальных и конечных газообразных реагентов.
Константа равновесия определяется при известных равновесных концентрациях реагирующих веществ либо по известной ?G° химической реакции
Произвольную обратимую химическую реакцию возможно обрисовать уравнением вида:
aA + bB U dD + eE
В соответствии с законом действующих массв несложном случае скорость прямой реакции связана с концентрациями исходных веществ уравнением
vпр = kпрСАа СВb ,
а скорость обратной реакции — с концентрациями продуктов уравнением
vобр = kобрСDd СEe .
При достижении равновесия эти скорости равны друг другу:
vпр = vобр
Отношение друг к другу обратной скорости реакций и констант прямой будет равняется константе равновесия:
| kпр СDd CЕ e ¾¾ = Kc = ¾¾¾¾ , kобр СAa CBb |
Так как это выражение основано на учёте количества реагентов и продуктов реакции, оно есть математической записью закона действующих весов для обратимых реакций.
Константа равновесия, выраженная через концентрации реагирующих веществ, именуется концентрационнойи обозначается Кс. Для более строгого рассмотрения направляться вместо концентраций применять термодинамические активностивеществ а = fC (где f — коэффициент активности). Наряду с этим речь заходит о так называемой термодинамической константе равновесия
| аDd аЕe Ка = ¾¾¾¾ . аAa аBb |
При малых концентрациях, в то время, когда коэффициенты активности исходных веществ и продуктов близки к единице, Кс и Ка фактически равны друг другу.
Константа равновесия реакции, протекающей в газовой фазе, возможно выражена через парциальные давления р веществ, участвующих в реакции:
| рDd рЕe Кр = ¾¾¾¾ . рAa рBb |
Между Кр и Кс существует соотношение, которое возможно вывести так. Выразим парциальные давления веществ через их концентрации посредством уравнения Менделеева — Клапейрона:
pV = nRT ,
откуда p = (n/V)RT = CRT .
Размерность констант равновесия зависит от метода выражения концентрации (давления) и стехиометрии реакции. Довольно часто она может приводить к недоумению, к примеру, в рассмотренном примере [моль-1м3] для Кс и [Па-1] для Кр, но в этом нет ничего неверного. При равенстве сумм стехиометрических коэффициентов продуктов и исходных веществ константа равновесия будет безразмерной.
Фазовое равновесие.
Фазовое равновесие- сосуществование термодинамически равновесных фаз, образующих неоднородную совокупность.
ФазаФ — совокупность частей совокупности, тождественных по физическим свойствам и химическому составу, находящихся между собой в отделённых и термодинамическом равновесии поверхностями раздела от вторых частей. Любая гомогенная совокупность однофазна, т. е. характеризуется отсутствием внутренних поверхностей раздела. Неоднородная совокупность содержит пара фаз (как минимум, две). В неоднородной совокупности фазы имеются внутренние поверхности раздела(время от времени именуемые межфазными границами).
Компонент- личное вещество, входящее в состав совокупности. Компонентом считается лишь то вещество, которое в принципе возможно выделено из совокупности и существует самостоятельно в течение достаточно долгого времени.
Число свободных компонентовсистемы К– это число компонентов, нужных для полного состава совокупности.Оно равняется неспециализированному числу компонентов минус число химических реакций, протекающих между ними.
Фазовые переходы- это переходы вещества из одного фазового состояния в второе при трансформации параметров, характеризующих термодинамическое равновесие.
ВариантностьсистемыС может быть представлена как число внешних условий (температура, давление, концентрация и др.), каковые экспериментатор может изменять, не изменяя наряду с этим числа фаз в совокупности.
правило фаз, есть следствием второго начала термодинамики,связывает число фаз, находящихся в равновесии, число свободных компонентов и число параметров, нужных для полного описания совокупности:
Число степеней свободы (вариантность) термодинамической совокупности, находящейся в равновесии, на которую из внешних факторов воздействуют лишь температура и давление, равно свободных компонентов минус число фаз плюс два:
С = К — Ф + 2
Фазовые диаграммы.
Изучение зависимости особенностей многоко