Пример. Отыскать точки разрыва функции. Выстроить чертеж.
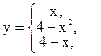в случае, если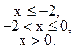 
Ответ. Конечно, что на промежутках и функция постоянна. Проверке подлежат лишь точки и .
Чтобы убедиться, что функция постоянна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в данной точке.
Разглядим точку .
.
Вычислим односторонние пределы
,
.
Так как односторонние пределы не совпадают, — точка разрыва функции.
Разглядим точку .
,
с,
,
— точка непрерывности функции, выполнены все условия непрерывности.
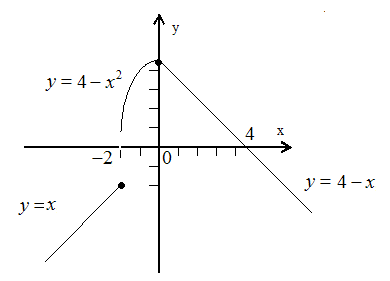
Рис. 1
Пример.Изучить поведение функции вблизи точки разрыва. Выстроить схематический чертеж.
.
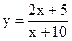Ответ. Область определения функции
. Точка разрыва .
Отыщем односторонние пределы
; 
.
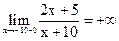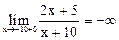Символ предела зависит от знаков знаменателя и числителя дроби. И в том и другом случае числитель , но знаменатель в пределе слева остается отрицательным, приближаясь к нулю, а в пределе справа, приближаясь к нулю, знаменатель остается хорошим. Схематичный чертеж представлен на рис. 2.
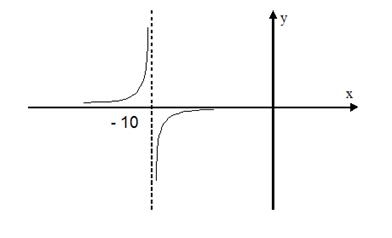
Рис. 2
дифференциал и Производная функции одной переменной
Пример. Пользуясь формулами дифференцирования, отыскать производные следующих функций: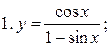 
.
Ответ.
1. 
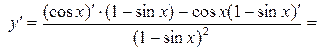
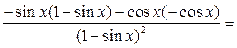
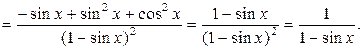
2. имеется сложная функция.
, где .
Производная сложной функции имеет форму
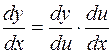либо .
Следовательно,
.
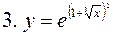— сложная функция.
, где , а ,
.
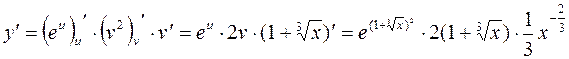Пример. Отыскать дифференциалы функций
1. ; 2.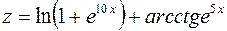 
, вычислить .
Ответ. Находим производную данной функции и, умножив ее на дифференциал свободной переменной, возьмём искомый дифференциал данной функции:
1. ;
2. 
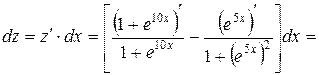
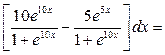
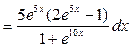
Полагая и , возьмём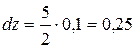 
.
Пример.Отыскать пределы, применяя правило Лопиталя
1. 
;
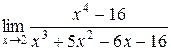2. 
;
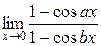3. 
;
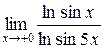4. 
.
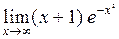Ответ. Убедившись, что имеет место неопределенность либо , используем после этого правило Лопиталя.
1. 
;
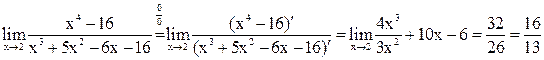2. 
;
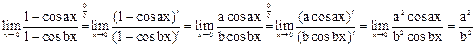— тут правило Лопиталя применено два раза.
3. 
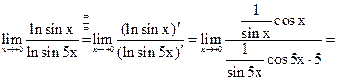
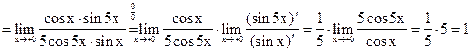
4. 
.
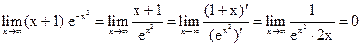построение поведения и Исследование функции её графика
Пример.Изучить функцию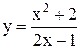 
и выстроить её график.
Ответ. 1. Функция выяснена и постоянна в промежутках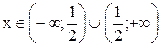 
.
2. Функция неспециализированного вида, поскольку
.
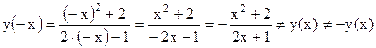3. График функции не пересекается с осью OХ, а с осью OY пересекается при x = 0,
y= -2, т.е. в точке В(0; -2).
4. Исследуем функцию на наличие асимптот.
а) Уравнение вертикальной асимптоты: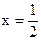 
.
Вычислим пределы функции при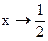 
слева и справа.
.
.
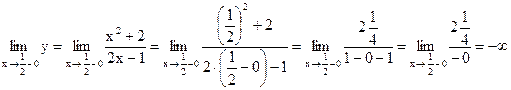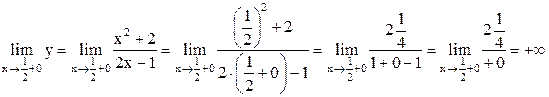б) Уравнение наклонной асимптоты имеет форму y = kx + b, где
.
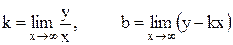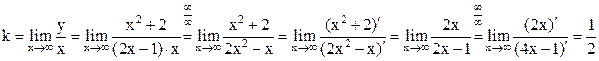
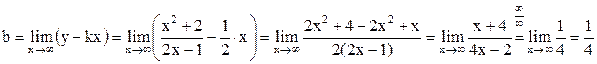
Так, уравнение наклонной асимптоты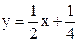 
.
5. Исследуем функцию на экстремум.
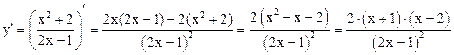
— точки, странные на экстремум.
Исследуем символ производной в промежутках, окружающих странные точки.
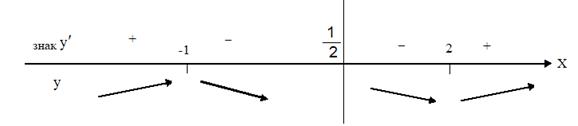
Рис. 3.
Взяли, что в точке х=-1 возрастание функции сменяется убыванием, следовательно, это точка максимума. В точке х=2 убывание сменяется возрастанием, следовательно, это точка минимума (рис. 3).
; 
.
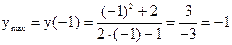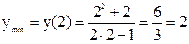6. Исследуем график функции на вогнутость и выпуклость.
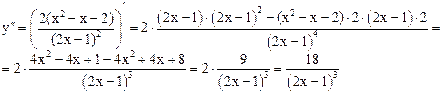
Точек перегиба нет, поскольку .
Исследуем символ второй производной в промежутках, где функция выяснена, (смотрите пункт 1. этого примера) (рис. 4).
Рис. 4.
Основываясь на взятых итогах изучения, строим график функции.
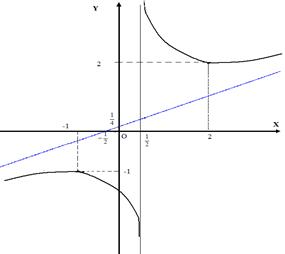
Рис. 5
Запомните таблицу главных формул и правил дифференцирования.
ТАБЛИЦА ПРОИЗВОДНЫХ
| № | № | ||||
|
|||||
|
|
||||
|
|
||||
|
|||||
|
|||||
|
|||||
|
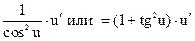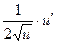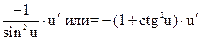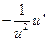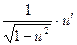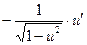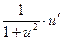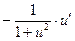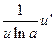Правила дифференцирования
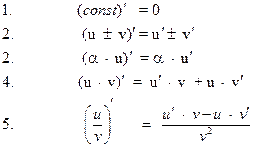
Контрольная работа 2
1. Отыскать указанные пределы, не пользуясь правилом Лопиталя.
| № | а | б | в |
| 1.01 |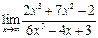 
|
|
|
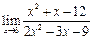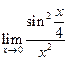| 1.02 |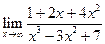 
|
|
|
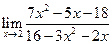| 1.03 |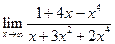 
|
|
|
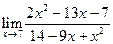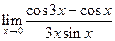| 1.04 |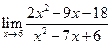 
|
|
|
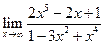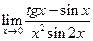| 1.05 |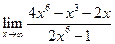 
|
|
|
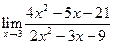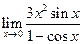| 1.06 |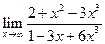 
|
|
|
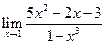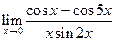| 1.07 |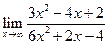 
|
|
|
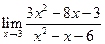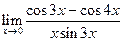| 1.08 |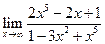 
|
|
|
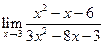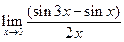| 1.09 |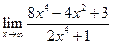 
|
|
|
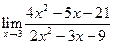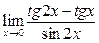| 1.10 |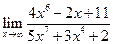 
|
|
|
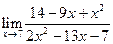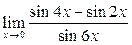| 1.11 |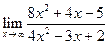 
|
|
|
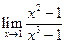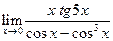| 1.12 |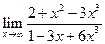
|
|
|
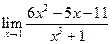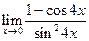| 1.13 |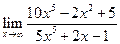 
|
|
|
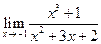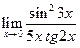| 1.14 |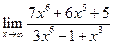 
|
|
|
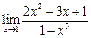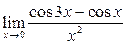| 1.15 |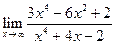 
|
|
|
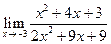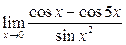| 1.16 |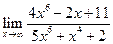 
|
|
|
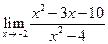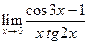| 1.17 |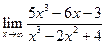 
|
|
|
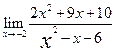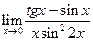| 1.18 |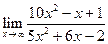 
|
|
|
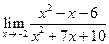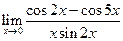| 1.19 |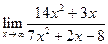 
|
|
|
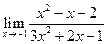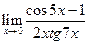| 1.20 |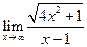 
|
|
|
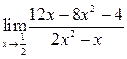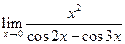2. Отыскать точки разрыва функции, если они существуют:
а) сделать чертеж функции;
б) сделать схематический чертеж около точки разрыва.
| № | № | ||
| 2.01 |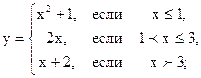 
|
2.11 |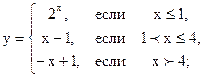 
|
| 2.02 |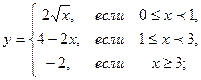 
|
2.12 |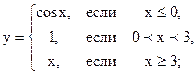 
|
| 2.03 |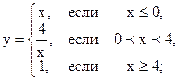 
|
2.13 |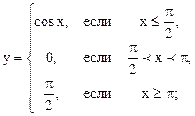 
|
| 2.04 |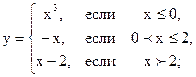 
|
2.14 |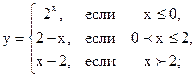 
|
| 2.05 |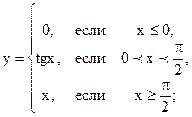 
|
2.15 |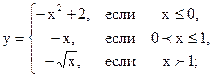 
|
| 2.06 |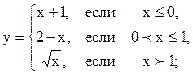 
|
2.16 |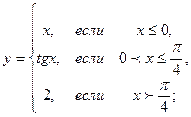 
|
| 2.07 |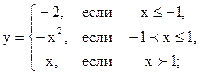 
|
2.17 |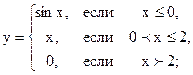 
|
| 2.08 |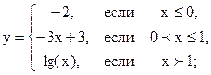 
|
2.18 |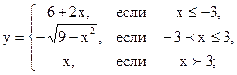 
|
| 2.09 |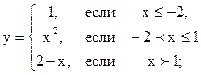 
|
2.19 |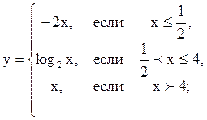 
|
| 2.10 |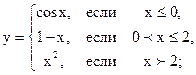 
|
2.20 |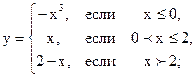 
|
3. Отыскать производные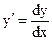 
данных функций.
| № | а | б | в |
| 3.01 |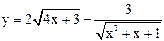 
|
||
| 3.02 |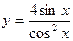 
|
||
| 3.03 |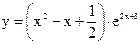 
|
||
| 3.04 |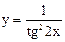 
|
||
| 3.05 |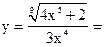 
|
|
|
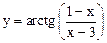| 3.06 |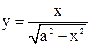 
|
|
|
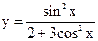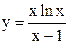| 3.07 |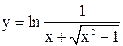 
|
||
| 3.08 |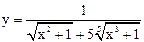 
|
||
| 3.09 |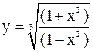 
|
|
|
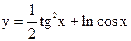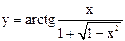| 3.10 |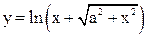 
|
||
| 3.11 |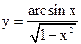 
|
||
| 3.12 |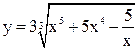 
|
||
| 3.13 |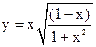 
|
|
|
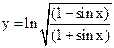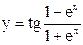| 3.14 |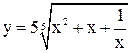 
|
|
|
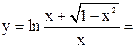| 3.15 | |||
| 3.16 |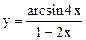 
|
||
| 3.17 |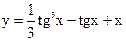 
|
||
| 3.18 |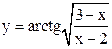 
|
||
| 3.19 |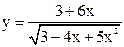 
|
|
|
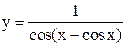| 3.20 |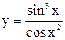 
|
4. Изучение функции:
а) отыскать экстремумы функции;
б) способами дифференциального исчисления изучить функцию
И, применяя результаты изучения, выстроить ее график.
| № | а | б | № | а | б |
| 4.01 |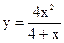 
|
4.11 |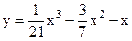 
|
|
|
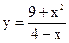| 4.02 |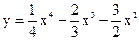 
|
|
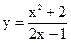4.12 |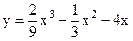 
|
|
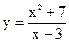| 4.03 |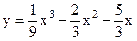 
|
|
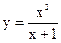4.13 |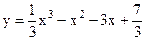 
|
|
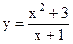| 4.04 |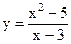 
|
4.14 |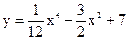 
|
|
|
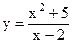| 4.05 |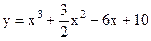 
|
|
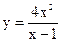4.15 |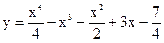 
|
|
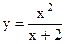| 4.06 |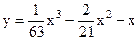 
|
|
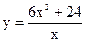4.16 |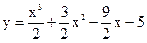 
|
|
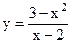| 4.07 |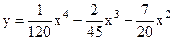 
|
|
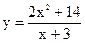4.17 |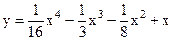 
|
|
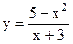| 4.08 |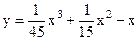 
|
|
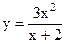4.18 |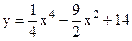 
|
|
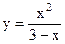| 4.09 |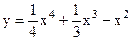 
|
|
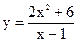4.19 |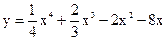 
|
|
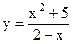| 4.10 |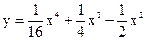 
|
|
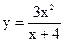4.20 |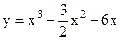 
|
|
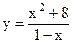