Лекция 9. Экстремумы функции нескольких переменных
Содержание лекций: Локальный экстремум. Нужное и достаточное условия экстремума. Условный экстремум функции нескольких переменных. Громаднейшее и мельчайшее значения функции в замкнутой ограниченной области.
Способ мельчайших квадратов.
Локальный экстремум ФНП
Пускай дана функция и = f(Р), РIDIRn и пускай точка Р0(а1, а2, …, ап) –внутренняя точка множества D.
Определение 9.4.
1) Точка Р0 именуется точкой максимума функции и = f(Р), в случае, если существует окрестность данной точки U(P0) I D такая, что для любой точки Р(х1, х2, …, хп)I U(P0) , Р¹Р0, выполняется условие f(P) ? f(P0) . Значение f(P0) функции в точке максимума именуется максимумом функции и обозначается f(P0) = max f(P) .
2) Точка Р0 именуется точкой минимума функции и = f(Р), в случае, если существует окрестность данной точки U(P0)I D такая, что для любой точки Р(х1, х2, …, хп)IU(P0), Р¹Р0, выполняется условие f(P) ³ f(P0) . Значение f(P0) функции в точке минимума именуется минимумом функции и обозначается f(P0) = min f(P).
максимума функции и Точки минимума именуются точками экстремумов, значения функции в точках экстремумов именуются экстремумами функции.
Как направляться из определения, неравенства f(P) ? f(P0) , f(P) ³ f(P0) должны быть выполнены лишь в некоей окрестности точки Р0 , а не во всей области определения функции, значит, функция может иметь пара однотипных экстремумов (пара минимумов, пара максимумов). Исходя из этого определенные выше экстремумы именуют локальными (местными) экстремумами.
Теорема 9.1.(нужное условие экстремума ФНП)
В случае, если функция и = f(х1, х2, …, хп) имеет экстремум в точке Р0, то ее частные производные первого порядка в данной точке или равны нулю, или не существуют.
Подтверждение. Пускай в точке Р0(а1, а2, …, ап) функция и = f(P) имеет экстремум, к примеру, максимум. Зафиксируем доводы х2, …, хп , положив х2=а2,…, хп = ап. Тогда и = семь дней(P) = f1((х1, а2, …, ап) имеется функция одной переменной х1. Так как эта функция имеет при х1 = а1 экстремум (максимум), то f1¢=0либо не существует при х1=а1 (нужное условие существования экстремума функции одной переменной). Но , значит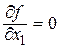 
либо не существует в точке Р0 – точке экстремума. Подобно возможно разглядеть частные производные по остальным переменным. ЧТД.
Точки области определения функции, в которых частные производные первого порядка равны нулю либо не существуют, именуются критическими точками данной функции.
Как направляться из теоремы 9.1, точки экстремума ФНП направляться искать среди критических точек функции. Но, как и для функции одной переменной, не любая критическая точка есть точкой экстремума.
Теорема 9.2.(достаточное условие экстремума ФНП)
Пускай Р0 – критическая точка функции и = f(P) и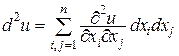 
– дифференциал второго порядка данной функции. Тогда
а) в случае, если d2u(P0) 0 при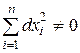 
, то Р0 – точка минимума функции и = f(P);
б) в случае, если d2u(P0) 0 при 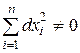, то Р0 – точка максимума функции и = f(P);
в) в случае, если d2u(P0) не выяснен по символу, то Р0 не есть точкой экстремума;
Эту теорему разглядим без доказательства.
Увидим, что в теореме не рассмотрен случай, в то время, когда d2u(P0) = 0 либо не существует. Это указывает, что вопрос о наличие экстремума в точке Р0 при таких условиях остается открытым – необходимы дополнительные изучения, к примеру, изучение приращения функции в данной точке.
В более подробных направлениях математики доказывается, что в частности для функции z = f(x, y) двух переменных, дифференциал второго порядка которой имеется сумма вида
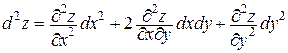
изучение наличия экстремума в критической точке Р0 возможно упростить.
Обозначим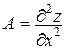 
, 
, 
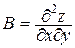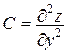. Составим определитель
.
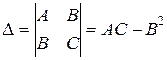Оказывается:
d2z 0 в точке Р0, т.е. Р0 – точка минимума, в случае, если A(P0) 0 и D(Р0) 0;
d2z 0 в точке Р0, т.е. Р0 – точка максимума, в случае, если A(P0) 0 , а D(Р0) 0;
в случае, если D(Р0) 0, то d2z в окрестности точки Р0 меняет символ и экстремума в точке Р0 нет;
в случае, если же D(Р0) = 0, то кроме этого требуются дополнительные изучения функции в окрестности критической точки Р0.
Так, для функции z = f(x, y) двух переменных имеем следующий метод (назовем его «методом D») отыскания экстремума:
1) Отыскать область определения D(f) функции.
2) Отыскать критические точки, т.е. точки из D(f), для которых и равны нулю либо не существуют.
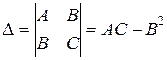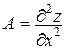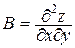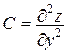3) В каждой критической точке Р0 проверить достаточные условия экстремума. Для этого отыскать , где , , и вычислить D(Р0) и А(Р0).Тогда:
в случае, если D(Р0) 0 , то в точке Р0 имеется экстремум, причем, в случае, если А(Р0) 0 – то это минимум, а вдруг А(Р0) 0 – максимум;
в случае, если D(Р0) 0, то в точке Р0 нет экстремума;
В случае, если D(Р0) = 0, то необходимы дополнительные изучения.
4) В отысканных точках экстремума вычислить значение функции.
Пример1.
Отыскать экстремум функции z = x3 + 8y3 – 3xy .
Ответ. Область определения данной функции – вся координатная плоскость. Отыщем критические точки.
, 
, 
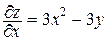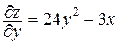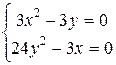? Р0(0,0) , 
.
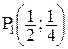Удостоверимся в надежности исполнение достаточных условий экстремума. Отыщем
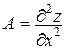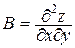= 6х, = -3, 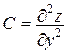= 48у и 
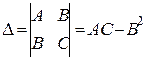= 288ху – 9.
Тогда D(Р0) = 288?0?0 – 9 = -9 0 , значит, в точке Р0 экстремума нет.
D(Р1) = 36-90 – в точке Р1 имеется экстремум, а так как А(Р1) = 3 0, то данный экстремум – минимум. Значит, min z= z(P1) =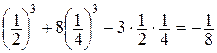 
.
Пример 2.
Отыскать экстремум функции .
Ответ: D(f) =R2 . Критические точки: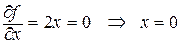 
; 
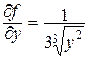не существует при у = 0, значит Р0(0,0) – критическая точка данной функции.
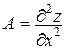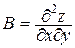= 2, = 0, =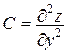 
, = 
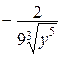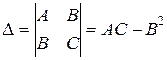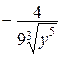, но D(Р0) не выяснено, исходя из этого изучение его символа нереально.
По данной же причине нереально применить теорему 9.2 конкретно – d2z в данной точке не существует.
Разглядим приращение функции f(x, y) в точке Р0. В случае, если Df =f(P) – f(P0)0 Р, то Р0 точка минимума, в случае, если же Df 0, то Р0 – точка максимума.
Имеем в нашем случае
Df = f(x, y) – f(0, 0) = f(0+Dx,0+Dy) – f(0, 0) = .
При Dx = 0,1 и Dy = -0,008 возьмём Df = 0,01 – 0,2 0, а при Dx = 0,1 и Dy = 0,001 Df = 0,01 + 0,1 0, т.е. в окрестности точки Р0 не выполняются ни условие Df 0 (т.е. f(x, y) f(0, 0) и тогда Р0 – не точка минимума). Значит, по определению экстремума, эта функция экстремумов не имеет.
Условный экстремум.
Рассмотренный экстремум функции именуют абсолютным, поскольку на доводы функции не налагаются никакие ограничения (условия).
Определение 9.2. Экстремум функции и = f(х1, х2, … , хп), отысканный при условии, что ее доводы х1, х2, … , хп удовлетворяют уравнениям j1(х1, х2, … , хп) = 0, …, jт(х1, х2, … , хп) = 0, где P (х1, х2, … , хп) I D(f), именуется условным экстремумом.
Уравнения jk(х1, х2, … , хп) = 0 , k = 1, 2,…, m, именуются уравнениями связи.
Разглядим функции z = f(x, y) двух переменных. В случае, если уравнение связи одно, т.е. , то отыскание условного экстремума свидетельствует, что экстремум ищется не во всей области определения функции, а на некоей кривой , лежащей в D(f) (т.е. ищутся не самые высокие либо самые низкие точки поверхности z = f(x, y), а самые высокие либо низкие точки среди точек пересечения данной поверхности с цилиндром , рис 5).
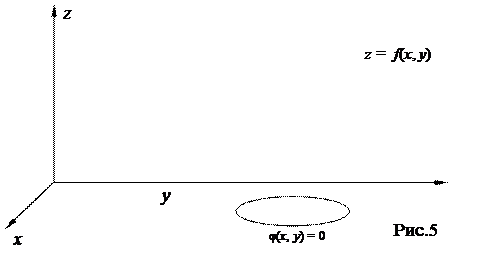
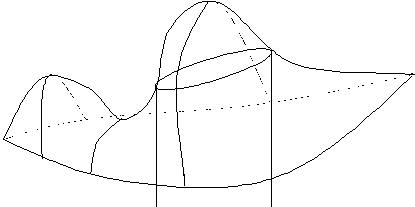
Условный экстремум функции z = f(x, y) двух переменных возможно отыскать следующим методом(способ исключения). Из уравнения выразить одну из переменных как функцию второй (к примеру, записать ) и, подставив это значение переменной в функцию , записать последнюю как функцию одной переменной (в рассмотренном случае ). Отыскать экстремум взятой функции одной переменной.
Пример 3:
Отыскать экстремум функции при условии .
Ответ. Уравнение связи имеется линейное уравнение довольно переменных х и у, из которого легко выразить одну переменную через другую, исходя из этого будем искать условный экстремум данной функции способом исключения.
Из уравнения выразим и подставим это выражение в функцию . Возьмём функцию одной переменной:
,
,
.
Отыщем экстремумы взятой функции . Область определения данной функции . Находим критические точки:
;
? ,
.
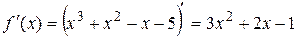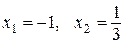Удостоверимся в надежности наличие экстремума в этих точках (смену символа производной при переходе через эти точки):
 |
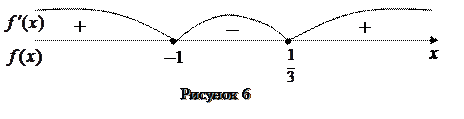Из рисунка 6 видно, что в точке функция имеет максимум, а в точке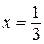 
эта функция имеет минимум, причем
,
.
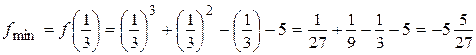Но точкам экстремума функции соответствуют точки одноименного условного экстремума исходной функции . Отыщем координаты этих точек:
при приобретаем , откуда имеем точку ;
при 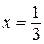приобретаем 
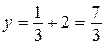, откуда имеем точку 
.
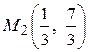Так, в точке функция имеет условный максимум
,
а в точке 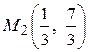эта функция имеет условный минимум
.
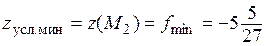Громаднейшее и мельчайшее значения функции в замкнутой ограниченной области (глобальный экстремум)
Пускай в замкнутой ограниченной области G выяснена постоянная функция и = f(Р). Тогда, как отмечалось в лекции 7, функция и = f(Р) в области G имеет громаднейшее и мельчайшее значения, т.е. $ точки Р1, Р2 I G такие, что РIG выполняется условие f(Р1) f(Р) f(Р2), где f(Р1) = f(Р) и
f(Р2) = .
Разумеется, точки Р1 и Р2 смогут лежать как в области G, так и на ее границе Г. В случае, если Рi – внутренняя точка, то f(Р) имеет в ней локальный экстремум. В случае, если Рi I Г, то это точка условного экстремума, где в роли уравнений связи выступают уравнения границы Г. Следовательно, точки глобального экстремума направляться искать среди критических точек функции, лежащих в области и на ее границе.
Для функции z = f(x, y) двух переменных отыскание громаднейшего и мельчайшего значений в замкнутой ограниченной области G возможно проводить по следующему методу.
1) Отыскать область определения D(f) функции и проверить, лежит ли область G в D(f).
2) Отыскать критические точки функции и отобрать из них принадлежащие области G (внутренние критические точки).
На каждом из участков границы Г, применяя его уравнение, отыскать критические точки, записав функцию z = f(x, y) как функцию одной переменной, исключив вторую переменную посредством уравнением разглядываемого участка границы. Наряду с этим необходимо отобрать лишь те точки, каковые принадлежат Г (граничные критические точки).
3) Отыскать «угловые» точки, т.е. точки соединения отдельных участков границы Г. Вычислить значения функции z = f(x, y) во всех взятых точках и выбрать из них громаднейшее и мельчайшее.
Замечание. В случае, если область ограничена одной замкнутой линией, то, при действий по указанному методу, к угловым точкам направляться отнести точки, соответствующие финишам отрезка трансформации переменной, довольно которой на данной кривой записана заданная функция. К примеру, для функции на границе круга имеет место представление функции в виде , критическая точка у=0, а граничными точками являются точки (0, 2) и (0, –2), т.к. .
Пример 4.
Отыскать громаднейшее и мельчайшее значения функции z = x2 + y2 в области G, ограниченной линиями у = х2 – 1, у = 3.
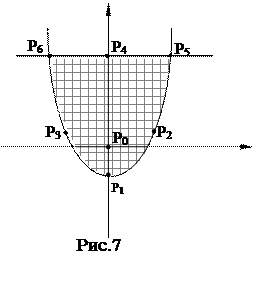
Ответ. D(z) = R2. Выстроим область G (рис.7).
Отыщем внутренние критические точки:
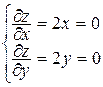, из этого Р0(0,0) –критическая точка, причем Р0IG.
Отыщем граничные критические точки. Разглядим участок границы, определяемый равенством у = х2 – 1. На данной линии функция z = x2 + y2 возможно записана в виде
z1 = x2 + (х2 – 1)2 = х4 – х2 + 1,
тогда z1¢= 4х3 – 2х =2х(2х2 – 1) = 0 , откуда
х = 0, либо х =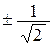 
.
При х = 0 имеем у = –1 (из равенства у = х2 – 1);
при х = 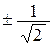возьмём у = – . Взяли точки Р1(0, -1), Р2 
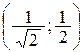и Р3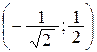 
, принадлежащие границе области G (рис.7).
На участке границы, заданном уравнением у = 3, функция z = x2 + y2 возможно записана в виде z2 = x2 + 9, тогда z2¢= 2х = 0, откуда х = 0. Тогда приобретаем точку Р4(0,3), которая кроме этого в собственности границе области G.
Отыщем «угловые» точки, для этого определим точки пересечения участков границы
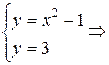Р5(2, 3) и Р6(–2, 3)
Вычислим значения функции во всех отысканных точках.
z(P0) = z(0,0) = 0, z(P1) = z(0,–1) = 1,
z(P2) = z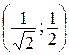 
= , z(P3) = z 
=
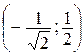z(P4) = z(0,3) = 9 , z(P5) = z(2,3)= 13, z(P6) = z(–2,3) = 13.
Значит z = z(±2,3)= 13 и .
Мы разглядели аналитический способ отыскания глобольного экстремума. Для функции двух переменных возможно кроме этого использован графический способ. Сущность его в следующем.
Для функции z = f(x, y) строится серия линий уровня f(x, y) = С для значений C0
Пример.5
Отыскать графически громаднейшее и мельчайшее значения функции
z = x2 + y – 1 в области G = {y = 0 , x = 1, y = x + 1}.
Ответ. Выстроим область G, это треугольник АВМ.
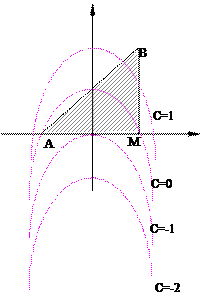Линии уровня заданной функции имеют уравнения x2 + y – 1 = С. Это имеется параболы y = (1 +С) – x2 . Выстроим серию этих парабол. Имеем
С1 = –2, у = –1– x2 ,
С2 = –1, у = – x2 ,
С3 = 0, у = 1– x2 ,
С4 = 1, у = 2 – x2 , и т.д.
Разумеется, первая точка, через которую линии уровня с возрастанием С «входят» в область, это точка (0,0). Значит, это и имеется точка мельчайшего значения функции, а так как на линии уровня, проходящей через эту точку, С = –1, то
.
Последняя точка области G, через которую пройдут линии уровня при возрастании С, будет вершина В треугольника АВМ, ее координаты (1,2), значит, z = z(1, 2) = 2.
Замечание.
В случае, если z = f(x, y) – линейная функция, то достаточно выстроить одну линию уровня, а после этого передвигать ее параллельно себе в направлении градиента функции. Точка входа в область (либо точка выхода при перемещении в направлении, противоположном направлению градиента) будет точкой мельчайшего значения, а точка выхода – точкой громаднейшего значения функции в заданной области.
Пример 6.
Отыскать громаднейшее и мельчайшее значения функции z = x + y в области G, ограниченной линиями у = х, у = (х – 2)2.
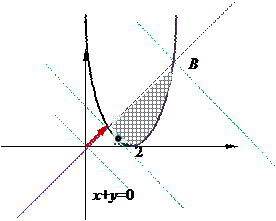Ответ. Выстроим область G. Функция z = x + y – линейная, значит, ее градиент в любой точке области определения сохраняет направление и равен grad z = = (1, 1) .
Разглядим одну из линий уровня заданной функции
х + у = С,
| А |
к примеру, при С=0, т.е. х + у = 0, и выстроим ее.
Увидим, что grad z перпендикулярен линии уровня х+у=0. Двигая линию уровня в направлении градиента, отыщем точку А входа линий уровня в область G и точку В выхода линий из области. Точка В имеется точка пересечения линий, образующих границу области:
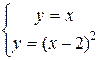? В(4,4).
Точка А – это точка кривой у = (х– 2)2, в которой касательная параллельна прямой х+ у =0, т.е. прямой у = –х. Тогда угловые коэффициенты касательной и этой прямой совпадают Угловой коэффициент прямой у = –х равен k = –1, а для касательной k = 2(x– 2).
Из равенства 2(x– 2) = –1 находим х = , тогда у = , так,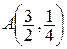 
. Тогд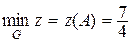а 
, а .