СОДЕРЖАНИЕ
Теоретическое введение.
Базы термодинамики и молекулярно-кинетической теории
(доц. А.Ю. Музычка)………………………………………………..4
1. Механический подход к описанию природы……………..4
2. Термодинамический подход к описанию
явлений природы………………………………………………5
3. Элементы молекулярно-статистической физики и кинетической теории…………………………………………………10
4. Теплоёмкости совершенного газа……………………………12
5. Вывод уравнения Пуассона……………………………….13
6. Элементарная теория теплоёмкостей совершенных газов…14
7. Элементы термодинамики жёстких тел………………….17
Лабораторная работа № 110
Определение отношения Сp/СV для воздуха способом Клемана-Дезорма
Теоретическое введение
БАЗЫ ТЕРМОДИНАМИКИ И МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
Механический подход к описанию природы
В механике объектом изучения являются тела, поведение которых описывается законами механического перемещения, т.е. тела, движущиеся как целое. Тела объединяются в механические совокупности. В качестве примеров механических совокупностей возможно привести солнечную совокупность, два шарика на пружинке и т.д. Более того, разглядывая поведение лишь одного тела, говорят, что имеется механическая совокупность, складывающаяся из одного тела.
Поведение совокупности с течением времени содержится в смене ее состояний. Чтобы обрисовать состояние совокупности материальных точек нужно задать их скорости и положения. Для описания состояния совокупности, в которую входят протяженные жёсткие тела, наровне с скоростями и положениями их центров весов нужно задать ориентации тел и их угловые скорости.
Так, задание состояния механической совокупности является заданием совокупности чисел, каждое из которых может измениться при трансформации состояния, т.е. с течением времени. Часто бывает так, что изменение одного числа влечет за собой изменение вторых чисел. К примеру, изменение положения центра весов жёсткого тела ведет к трансформации положений вторых его материальных точек. Дадим определение: совокупность свободных размеров, конкретно определяющих состояние механической совокупности, именуется совокупностью динамических переменных. Отсюда ясно, что эволюция совокупности, т.е. смена ее состояний с течением времени, описывается как изменение с течением времени ее динамических переменных.
Всё, что возможно выражено через динамические переменные, является функцией механического состояния совокупности. Одной из таких функций есть механическая энергия, т.е. сумма потенциальной и кинетической энергий. Еще одно определение: степенью свободы механической совокупности именуется динамическая переменная, от которой зависит полная механическая энергия совокупности.
Приведем несложной пример. Разглядим механическую совокупность, складывающуюся из одной материальной точки в однородном и изотропном пространстве, т.е. в отсутствие каких бы то ни было силовых полей. Ясно, что в случае, если на тело не действуют никакие силы, то ее потенциальная энергия не изменяется при переходе из одного положения в второе и возможно принята за 0. Совокупность описывается шестью динамическими переменными: тремя пространственными координатами и тремя компонентами скорости. Но, потому, что, полная механическая энергия совокупности представляет собой лишь кинетическую энергию, то у совокупности лишь три степени свободы, которыми являются компоненты скорости по взаимно перпендикулярным осям: vx,без сомнений, vz.
Механика ставит собственной задачей правильное описание эволюции механической совокупности и дает ответ на вопрос, что для этого нужно. Нужно и достаточно совершенно верно задать начальное состояние и стационарные поля сил, действующих на тела совокупности.
Термодинамический подход к описанию явлений природы.
Термодинамические состояния.
Достаточно непредвзято посмотреть на окружающий нас мир, дабы сделать вывод о том, что механический подход не есть исчерпывающим при его описании. Протяженные тела, каковые нас окружают, довольно часто неподвижны, и с позиций механики про них сообщить больше нечего. Однако, яркий опыт убеждает нас, что они смогут быть в различных состояниях: вода, помещенная в сосуд, возможно или весьма холодной, или прохладной, или горячей, или в виде крутого кипятка. Эти состояния не являются состояниями в механическом смысле. Слова «горячее», «холодное», понятные для любого из нас, по большому счету не имеют смысла в механике.
Совокупности, состояния которых не смогут быть абсолютно обрисованы в механике, именуются термодинамическими (ТД) совокупностями. Параметры, дополнительные по отношению к механическим, именуются термодинамическими параметрами. Полная совокупность ТД-параметров совокупности обрисовывает её термодинамическое состояние.
Совокупности, разглядываемые в термодинамике, — это макроскопические тела, и ТД-параметры являются их макроскопические особенности. Все они смогут быть оценены конкретно посредством органов эмоций человека. Термодинамика изучает явления и макроскопические свойства, не интересуясь их микроскопической природой.
В «фокусе» термодинамического рассмотрения находится неподвижное тело (ТД-совокупность), которое обменивается энергией с окружением. Наряду с этим механическое состояние тела в процессах этого обмена не изменяется, в то время как механическое состояние окружения может изменяться. Термодинамика обрисовывает процессы обмена энергией в таковой постановке задачи и связанные с этим трансформации ТД-состояния разглядываемой совокупности.
Мы будем вычислять, что окружение и система не обмениваются собственными частями, т.е. нет массообмена. В этом случае обмен энергией производится двумя методами: в ходе работы и в ходе теплообмена.
Работой именуется процесс обмена энергией, сопровождаемый механическим перемещением.Количество энергии, переданной от совокупности окружению в этом ходе, также именуется работой А. Как видим, слово «работа» используется в двух различных смыслах.
Работой именуется процесс обмена энергией, сопровождаемый трансформацией внешних параметров ТД-совокупности.
Процесс обмена энергии, не связанный с трансформацией внешних параметров ТД-совокупности, именуется теплообменом.
Температура.
Заданное ТД-состояние определяет все физические размеры, которые связаны с этим состоянием, т.е. функции состояния. Из изложенного выше направляться, что состояние не может быть задано одним параметром. Следовательно, состояния и-функции – это функции нескольких доводов. Из двух параметров равновесного газа p и V возможно неестественным образом сконструировать нескончаемое множество функций, физический суть которых будет неясен либо по большому счету его не будет. Становление термодинамики было связано с открытием функций состояния, имеющих физический суть.
Теплообмен между двумя ТД-совокупностями вероятен, в случае, если их приводят в тепловой контакт. ТД-совокупность, которая не находится в тепловом контакте ни с какой второй, именуется адиабатически изолированной. Две равновесные совокупности, приведенные в тепловой контакт между собой, смогут обмениваться теплом, а смогут и не обмениваться. В последнем случае говорят, что они находятся в равновесии между собой, либо, иначе говоря что у них однообразная температура. Для каждой равновесной ТД-совокупности существует функция ее ТД-параметров, которая для всех совокупностей, находящихся в равновесии между собой, имеет одно да и то же значение; эта функция именуется температурой.
Так, температура возможно выяснена лишь в равновесном состоянии ТД-совокупности. Дабы понятия «громадная» и «меньшая температура» имели строго определенный суть, нужно добавить, что при получении телом тепла при постоянных внешних параметрах его температура возрастает.
Из опыта известен следующий факт: в случае, если зафиксировать все внешние параметры совокупности в термостате, то в ней со временем установится единственно вероятный комплект равновесных внутренних параметров. Следовательно, в равновесном ТД-состоянии все внутренние параметры конкретно определяются температурой и внешними параметрами.
Соотношение, связывающее температуру, внешние и внутренний параметры равновесного ТД-состояния, именуется уравнением состояния. В термодинамике совершенным газом именуется совокупность, уравнением состояния которой есть уравнение Менделеева-Клапейрона:
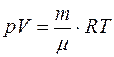
Итоги обзора ТД-подхода.
Подобно механике термодинамика, обрисовывающая поведение термодинамических совокупностей, есть независимой физической дисциплиной благодаря двум событиям: во-первых, в ее рамках установлен метод описания состояния изучаемых совокупностей; во-вторых, установлена совокупность теорем, которым подчиняется любой переход между состояниями. Среди этих теорем нас в данном цикле работ будет интересовать лишь одна: первый закон ТД.
И статистической физики
Главное положение молекулярно-кинетической теории (МКТ) строения вещества, рожденное еще в Греции как очень способная догадка, о том, что все макроскопические тела складываются из огромного количества микроскопических, во второй половине XIX и в начале XX столетий отыскало собственный экспериментальное подтверждение.
Оказалось, что характерная масса макромира, равная одному грамму, больше, чем масса одного атома водорода, равная одной ядерной единице, в NA раз, где NA@6?1023 – число Авогадро. Это число есть характерным числом, показывающим, какое число микроскопических частиц образовывает макроскопическое тело.
Любое макроскопическое тело МКТ принципиально разглядывает как механическую совокупность. В частности, самый простое по особенностям макроскопическое тело, которым есть совершенный газ, МКТ определяет следующим образом. Совершенным именуется газ, для которого суммарная потенциальная энергия сотрудничества молекул, являющаяся функцией их обоюдного размещения, все время пренебрежимо мелка если сравнивать с их суммарной кинетической энергией теплового перемещения, а размеры молекул пренебрежимо мелки по сравнению со средним расстоянием между ними.
Чем выше температура газа и ниже его давление, тем ближе по своим особенностям настоящий газ к совершенному. Многие газы (к примеру, инертные газы, Н2, О2, N2 и др.) можно считать совершенными уже при обычных условиях (давление р=105 Па, Т=273 К) а также при более низких температурах.
Но, принимая в расчет огромное количество материальных тел, из которых состоит механическая совокупность «макроскопическое тело», МКТ по отношению к подобной системе совершенно верно кроме этого принципиально отказывается от главной задачи механики, которая была сформулирована в конце пункта 1.
С позиций МКТ все внутренние ТД-функции и параметры ТД-состояний являются механические размеры, усредненные по всем микрочастицам, входящим в совокупность. Задачей МКТ есть расчет одних макроскопических параметров и выражение через вычисленные всех черт макросистемы. Эту задачу МКТ решает отнюдь не способами механики, а применяя аппарат теории возможности и собственную совокупность постулатов. Исходя из этого МКТ именуется кроме этого классической статистической физикой.
Из всей совокупности постулатов стат. физики нас будут интересовать лишь закон о равном распределении внутренней энергии по степеням свободы: в состоянии ТД-равновесия на каждую степень свободы макроскопической совокупности в среднем приходится однообразная порция внутренней энергии, равная kT/2. Тут k=1.38?10-23 Дж/К – постоянная Больцмана. Необходимо осознавать, что «в среднем» – это не просто взяли неспециализированную U и поделили на количество степеней свободы совокупности. Это значит то значение, около которого с течением времени «пляшет» энергия данной степени свободы. Т.е. тут под сглаживанием понимается сглаживание по времени.
Во-первых, последний постулат делает прозрачным суть безотносительной температуры: выясняется полная температура – мера энергии теплового перемещения, приходящейся на одну степень свободы в состоянии теплового равновесия. Во-вторых, он разрешает скоро вычислить внутреннюю энергию совершенного газа в равновесном состоянии.
Пускай совершенный газ складывается из N молекул с числом степеней свободы одной молекулы, однообразным для всех молекул и равным i. Т.к. сотрудничеством между молекулами возможно пренебречь, то сумма личных степеней свободы молекул и имеется полное число степеней свободы, которое равняется N?i. Из этого внутренняя энергия совершенного газа
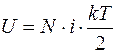
Как мы знаем N=n?NA, где число молей n=m/m, где m — молярная масса газа, а т – масса газа. Следовательно
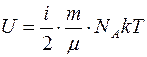
Произведение NA?k= R (универсальная газовая постоянная). Следовательно
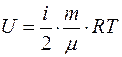
Из этого дифференциал внутренней энергии определенного количества определенного совершенного газа
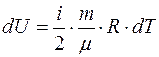
Вывод уравнения Пуассона
При адиабаты I-й закон ТД принимает вид:
0=СV?dT+р?dV.
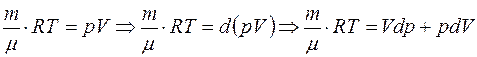
Из соотношения Майера
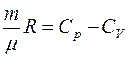
Следовательно
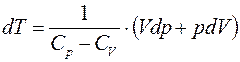
Подставим в I-й закон:
Раскроем скобки и приведем подобные члены по дифференциалам p и V:
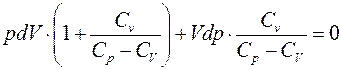
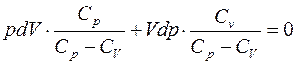
Поделим это уравнение на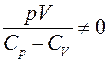 
. В следствии возьмём:
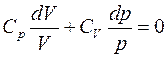
Поделим на CV¹0:
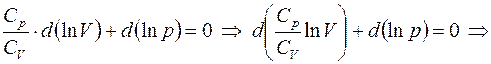
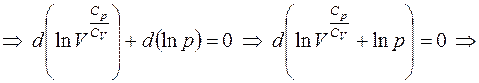
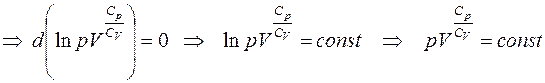
Обозначим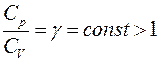 
— показатель адиабаты, следовательно,
PVg=const
Совершенных газов
Разглядим вероятные случаи.
1) Одноатомный совершенный газ.
Одноатомную молекулу возможно представить как материальную точку, движущуюся в однородном и изотропном пространстве. Следовательно, она имеет три степени свободы. В этом случае показатель адиабаты
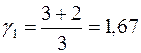
2) Двухатомный совершенный газ, складывающийся из твёрдых молекул.
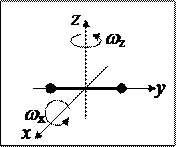Кинетическая энергия одной молекулы связана, во-первых, с поступательным перемещением центра весов молекулы. Разумеется, что эти перемещения имеет три степени свободы. Во-первых, молекула совершает вращательное перемещение около центра весов молекулы. Это перемещение возможно разглядывать как суперпозицию вращений около трех взаимно перпендикулярных осей x,y,z, совершённых через центр весов молекулы. Тогда с каждой из осей связана энергия
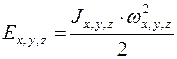
где Ji – осевые моменты инерции, а wi – соответствующие угловые скорости. В случае, если оси вращения направить так, как указано на рисунке, то момент инерции оси, совпадающей с осью молекулы, равен 0. Следовательно, вместо трех вращательных степеней свободы реализуется лишь две. Так, i=3+2=5. Следовательно,
.
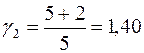В большинстве многоатомных молекулах с числом атомов громадным двух, атомы не «выстраиваются» по одной прямой (исключением есть, к примеру углекислый газ СО2). Исходя из этого вращательных степеней свободы будет уже три, тогда i=6 и для твёрдых молекул
.
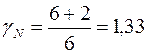3) Двухатомный совершенный газ, складывающийся из нежёстких молекул.
Несложнее всего такую молекулу представить как одномерный осциллятор, т.е. точечные веса атомов, соединенные пружинкой, которая может лишь сжиматься и разжиматься, но не имеет возможности изгибаться. С колебательным перемещением связана кинетическая энергия перемещения атомов относительно друг друга (одна степень свободы) и потенциальная энергия сжатой пружины, которая связана с расстоянием между атомами (еще одна степень свободы). Так, колебательное перемещение «занимает» две степени свободы. Наряду с этим сохраняются 5 степеней свободы поступательного и вращательного перемещения. Итого i=5+2=7, следовательно
.
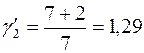С позиций классической механики не существует обстоятельств, каковые делали бы связь между атомами в молекуле полностью твёрдой. Исходя из этого классическая физика для двухатомного газа предвещает значение g=1,29 при любой температуре. Но молекула есть микроскопическим объектом и подчиняется законам не хорошей, а квантовой механики. По этим законам для того, вынудить осциллятор двигаться, ему необходимо сказать порцию энергии, определяемую собственной частотой колебаний осциллятора n0 по следующей формуле:
De=hn0
где постоянная Планка h=6,63?10-34 Дж?с. Тепловые возбуждения смогут «заселить» квантовый осциллятор лишь при условии
kT @ hn0
Но личные частоты молекулярных «пружинок» огромны, и чтобы выполнялось это соотношение, температура обязана достигать ~103 К. При комнатных температурах
kT
исходя из этого связь между атомами в молекуле есть «замороженной» и полностью твёрдой. Так, квантовая механика предвещает значение g=1,4 при комнатной температуре.
Исследуемый в одной из лабораторных работ сборника воздушное пространство есть двухатомным газом при комнатной температуре, и исходя из этого, делая работу, студент сам может проверить справедливость хорошего либо квантового предсказания.
Лабораторная работа № 110
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ Ср/СV ДЛЯ ВОЗДУХА СПОСОБОМ КЛЕМАНА-ДЕЗОРМА
Цель лабораторной работы
Целью данной лабораторной работы есть усвоение закономерностей молекулярной термодинамики и физики.
Задачи лабораторной работы
Задачей работы есть определение отношения теплоемкостей совершенного газа при постоянном давлении и при постоянном количестве. На основании взятой в опыте величины студент обязан выяснить количество степеней свободы, приходящееся на одну молекулу совершенного газа. Иначе говоря наименование данной работы возможно было бы сформулировать так: «Экспериментальное определение числа степеней свободы одной молекулы исследуемого совершенного газа».
принадлежности и Приборы
Лабораторный комплекс ЛКТ-5, стеклянный баллон, груша-помпа, мембранный манометр, силиконовые шланги, тройники для шлангов.
Вывод расчётной формулы
Изложим неспециализированную канву способа Клемана-Дезорма.
В случае, если в сосуд количеством V02 с установившимся атмосферным давлением подкачать мало газа, то давление в сосуде р1 увеличиться атмосферного (р0), а температура через некое (достаточно маленькое) время станет равной комнатной. Так, мы возьмём равновесное состояние 1 любой порции газа, находящегося в сосуде. Нас будет интересовать та порция, которая останется в баллоне по окончании последующего стравливания газа. Обозначим её количество вещества n (на рисунке количество вещества стравленного газа обозначено Dn) и её количество до стравливания (т.е. в состоянии 1) V1.
Стравливание происходит весьма скоро в следствии резкого открывания выходного крана. Когда давление упадет до давления р0, кран кроме этого быстро закрывают. Интересующая нас порция в следствии стравливания занимает место ушедшего из баллона газа, т.е. расширяется. Будем вычислять, что из-за быстроты процесса расширяющийся газ не успевает обменяться теплом с окружением, и его расширение случится адиабатически. Наряду с этим, не обращая внимания на быстроту, процесс будем вычислять равновесным. Состояние газа по окончании адиабатического расширения назовем состоянием 0. Разумеется, что в этом состоянии температура газа будет меньше комнатной.
С течением времени газ в закрытом сосуде будет нагреваться и его температура достигнет комнатной. А потому, что количество газа останется неизменным, то давление повысится до значения р2. Состояние по окончании изохорного нагрева назовем состоянием 2.
Обрисованные процессы и состояния в осях представлены на следующем рисунке
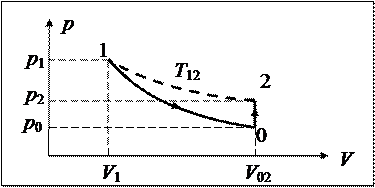
Пунктиром обозначена изотерма комнатной температуры T12, на которой лежат состояния 1 и 2.
Состояния 1 и 0 связаны уравнением Пуассона:
.
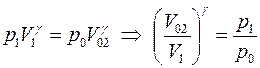Состояния 1 и 2 связаны законом изотермы:
.
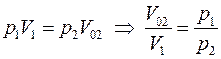Подставляя отношение количеств в прошлое соотношение, приобретаем:
.
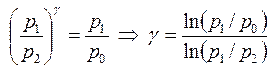Такова сущность способа Клемана-Дезорма, разрешающего по трём совершенно верно измеренным давлениям: р0, р1, р2выяснить показатель адиабаты g, что равен искомому отношению теплоёмкостей:
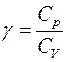
(см. теоретическое введение).
В опыте прямо измеряются избыточные давления
и ? i=1,2.
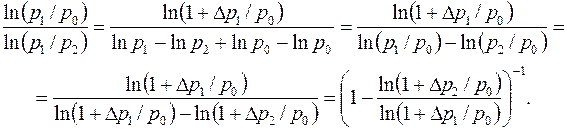
Итак:
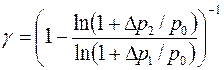(1)
К сожалению, настоящий физический опыт не разрешает применять приведённое выражение g в качестве расчетной формулы при единичном измерении Dр1, Dр2. Этому мешают сходу два события.
Во-первых, для справедливости выражения нужно, дабы при стравливании остающийся газ расширялся равновесно. Равновесными именуются процессы, воображающие временную последовательность равновесных состояний. Конкретно равновесные процессы изображаются на pV-диаграмме. Полностью совершенно верно они реализуются, в случае, если скорость их протекания вечно мелка. Чем меньше избыточное давление газа, тем ближе настоящий процесс его расширения при стравливании к равновесному. Исходя из этого формула (1) «трудится» лишь при .
Во-вторых, состояние 0, в то время, когда адиабатическое расширение оставшегося газа закончилось, а нагрев ещё не начался, предугадать нереально. Или кран будет перекрыт раньше, чем в сосуде установится давление (что мало возможно), или (вероятнее, так оно и будет) позднее. pV-диаграммы двух этих случаев представлены ниже.
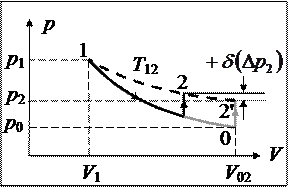
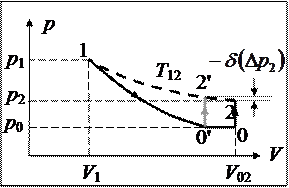
Из картинок видно, что настоящее значение Dр2 в первом случае будет больше, а во втором – меньше, чем то, которое входит в формулу (1). Т.е. она выполняется при условии , где t – настоящее время стравливания, а t* — то, которое необходимо по способу.
Исходя из этого в качестве расчётной формулы мы примем соотношение:
.
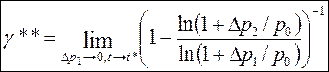Расчётная формула для того чтобы вида предъявляет определённые требования к методике опыта. Нужно проводить серию измерений Dр2 при монотонно изменяющихся Dр1 и t, с тем дабы распознать тенденцию в трансформации показателя адиабаты, рассчитываемого по формуле (1). А после этого способом экстраполяции определять подлинное значение g**.
Подводя итог пара слов о точности вычислений. В данной работе исследуется воздушное пространство, воображающий собой смесь молекулярного азота N2 и молекулярного кислорода О2. Т.е. исследуемый совершенный газ есть двухатомным. В теоретическом введении указывалось, что в этом случае необходимо решать задачу экспериментально обоснованного выбора между двумя вероятными значениями: g=1.29, предвещаемого хорошей теорией и g=1.40, предвещаемого квантовой теорией. Также, между 1.29 и 1.40 находится значение g=1.33 многоатомных нелинейных твёрдых молекул. Чтобы распознать отличие между этими, достаточно родными, числами и отношения , и соответствующие логарифмы должны вычисляться с точностью до третьего символа по окончании запятой. Исходя из этого упрощающие формулы типа
в рабочем диапазоне избыточных давлений мм рт.ст. при атмосферном давлении р0=750 мм рт.ст. использовать запрещено.
СОДЕРЖАНИЕ
Теоретическое введение.
Базы термодинамики и молекулярно-кинетической теории
(доц. А.Ю. Музычка)………………………………………………..4
1. Механический подход к описанию природы……………..4
2. Термодинамический подход к описанию
явлений природы………………………………………………5
3. Элементы молекулярно-статистической физики и кинетической теории…………………………………………………10
4. Теплоёмкости совершенного газа……………………………12
5. Вывод уравнения Пуассона……………………………….13
6. Элементарная теория теплоёмкостей совершенных газов…14
7. Элементы термодинамики жёстких тел………………….17
Лабораторная работа № 110
Определение отношения Сp/СV для воздуха способом Клемана-Дезорма
Теоретическое введение
БАЗЫ ТЕРМОДИНАМИКИ И МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
Механический подход к описанию природы
В механике объектом изучения являются тела, поведение которых описывается законами механического перемещения, т.е. тела, движущиеся как целое. Тела объединяются в механические совокупности. В качестве примеров механических совокупностей возможно привести солнечную совокупность, два шарика на пружинке и т.д. Более того, разглядывая поведение лишь одного тела, говорят, что имеется механическая совокупность, складывающаяся из одного тела.
Поведение совокупности с течением времени содержится в смене ее состояний. Чтобы обрисовать состояние совокупности материальных точек нужно задать их скорости и положения. Для описания состояния совокупности, в которую входят протяженные жёсткие тела, наровне с скоростями и положениями их центров весов нужно задать ориентации тел и их угловые скорости.
Так, задание состояния механической совокупности является заданием совокупности чисел, каждое из которых может измениться при трансформации состояния, т.е. с течением времени. Часто бывает так, что изменение одного числа влечет за собой изменение вторых чисел. К примеру, изменение положения центра весов жёсткого тела ведет к трансформации положений вторых его материальных точек. Дадим определение: совокупность свободных размеров, конкретно определяющих состояние механической совокупности, именуется совокупностью динамических переменных. Отсюда ясно, что эволюция совокупности, т.е. смена ее состояний с течением времени, описывается как изменение с течением времени ее динамических переменных.
Всё, что возможно выражено через динамические переменные, является функцией механического состояния совокупности. Одной из таких функций есть механическая энергия, т.е. сумма потенциальной и кинетической энергий. Еще одно определение: степенью свободы механической совокупности именуется динамическая переменная, от которой зависит полная механическая энергия совокупности.
Приведем несложной пример. Разглядим механическую совокупность, складывающуюся из одной материальной точки в однородном и изотропном пространстве, т.е. в отсутствие каких бы то ни было силовых полей. Ясно, что в случае, если на тело не действуют никакие силы, то ее потенциальная энергия не изменяется при переходе из одного положения в второе и возможно принята за 0. Совокупность описывается шестью динамическими переменными: тремя пространственными координатами и тремя компонентами скорости. Но, потому, что, полная механическая энергия совокупности представляет собой лишь кинетическую энергию, то у совокупности лишь три степени свободы, которыми являются компоненты скорости по взаимно перпендикулярным осям: vx,vy, vz.
Механика ставит собственной задачей правильное описание эволюции механической совокупности и дает ответ на вопрос, что для этого нужно. Нужно и достаточно совершенно верно задать начальное состояние и стационарные поля сил, действующих на тела совокупности.