ИЗУЧЕНИЕ НЕЛИНЕЙНЫХ СОВОКУПНОСТЕЙ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ АМПЛИТУДНО-ЧАСТОТНЫМ СПОСОБОМ
Ц Е Л Ь Р А Б О Т Ы – изучение нелинейной совокупности автоматического регулирования одним из распространенных инженерных способов – амплитудно-частотным способом.
9.1. краткие сведения из теории
Широкое распространение при расчёте и инженерном исследовании нелинейных совокупностей регулирования взяли амплитудно-частотный способ, предложенный Л.С. Гольдфарбом и являющийся приближенным способом изучения нелинейных совокупностей.
Амплитудно-частотный способ предполагает гармонический темперамент колебаний в нелинейной совокупности. В базе способа лежит понятие эквивалентного комплексного коэффициента усиления нелинейного элемента. Нелинейная динамическая совокупность (рис.8.1) условно разбивается на линейную часть с передаточной функцией
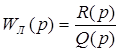(9.1)
и нелинейный элемент
. (9.2)
Предполагается, что линейная часть владеет свойством фильтра, т.е. при происхождении периодических колебаний все высшие гармоники подавляются линейной частью совокупности. Тогда на ее выходе, соответственно, на выходе нелинейного элемента, переменная х будет иметь форму колебаний, близкой к синусоидальной:
. (9.3)
Таким свойством фильтра владеет большая часть настоящих контуров управления.
При симметричных установившихся одночастотных колебаниях гармоническая линеаризация пребывает в замене нелинейности F(x) выражением
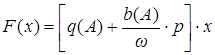, (9.4)
где
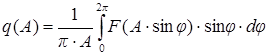, (9.5)
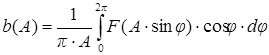. (9.6)
При отыскании периодического ответа для переменной x в форме (9.3) (малоизвестны А и ) возможно, имея ввиду свойства фильтра, для совокупности по рис.8.1 с учетом (9.4) записать гармонически линеаризованное уравнение динамики совокупности:
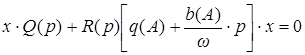. (9.7)
Периодическое синусоидальное ответ дифференциального уравнения (9.7) будет соответствовать паре чисто мнимых корней характеристического уравнения:
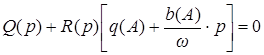. (9.8)
Исходя из этого для отыскания размеров А и искомого синусоидального ответа положим p=jw. Тогда уравнение (9.8) примет вид:
, (9.9)
откуда направляться:
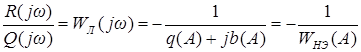, (9.10)
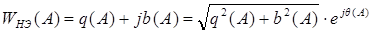. (9.11)
Равенство (9.10) является условием гармонического баланса либо условие происхождения автоколебаний. Аналитическое ответ уравнения (9.10) довольно часто воображает серьёзные трудности. Графоаналитический способ ответа этого уравнения нагляден и несложен: на комплексной плоскости строят годограф линейной части и годограф ; точки пересечения этих годографов говорят о возможности автоколебаний и определяют их амплитуду и частоту.
Точка пересечения годографов свидетельствует только возможность существования автоколебаний. Исходя из этого, исследуя точки пересечения годографов, необходимо выяснить, устойчивы ли соответствующие им автоколебания (на фазовом портрете — предельные циклы). Значение частоты устойчивых колебаний отсчитывается на годографе , а амплитуда A отсчитывается на годографе .
В большинстве случаев по окончании амплитуды и определения частоты вероятных автоколебаний целесообразно проверить амплитуду третьей гармоники. Если не выполняется соотношение
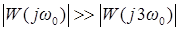, (9.12)
то способ Гольдфарба неприменим, а правильнее, существенно возрастает погрешность способа.
9.2. Порядок исполнения работы
1. Собрать схему, приведенную на рис. 9.1.
2. В качестве нелинейного элемента НЭ применять “совершенное реле”. Установить следующие значения параметров элементов: Т1 = 0.8 с; Т2 = 0.1 с; k1 = 1.2; k2 = 1.
3. Замечать фазовые траектории и соответствующие им переходные процессы при х0 = 2, v0 = 0, tмод = 25 с. Полученные графики фазовых переходных процессов и траекторий нужно представить в отчете.
4. По взятым в следствии моделирования графикам выяснить экспериментальные значения параметров автоколебаний.
5. В качестве нелинейного элемента НЭ (рис.9.1) применять “реле с гистерезисом”, параметры которого забрать из прошлой работы (рис.8.5).
6. Замечать фазовые траектории и соответствующие им переходные процессы при х0 = 2, v0 = 0, tмод = 25 с. Полученные графики фазовых переходных процессов и траекторий нужно представить в отчете.
7. По взятым графикам выяснить экспериментальные значения параметров автоколебаний.
8. Посредством графоаналитического способа Гольдфарба для разрешённой системы найти параметры автоколебаний и сравнить их с экспериментальными.
Рисунок 9.1. Модель нелинейной САУ.
9.3. СОДЕРЖАНИЕ ОТЧЕТА
В отчете о лабораторной работе нужно привести:
1. Наименование и цель лабораторной работы.
2. Схему модели нелинейной САУ.
3. Графики фазовых траекторий и соответствующие им графики переходных процессов.
4. Параметры автоколебаний, каковые выяснены экспериментально.
5. Графоаналитический расчет параметров автоколебаний в нелинейной совокупности и сравнение результатов с взятыми экспериментально.
6. Выводы по лабораторной работе.