Главным моментом ответа задач есть построение бортиков и плоскости. Для построения плоскости употребляется функция DrawPool, а для построения бортиков – DrawBorder.
Для поворота задачи и решения перемещения объектов в способах прорисовки поверхности октаэдра с диффузионной и зеркальной моделями освещения употреблялись аффинные преобразования (приложение Г). Положения октаэдра задается функцией SetPos, изменение положения октаэдра в зависимости от скорости – Move, а начальные параметры задаются в функции SetV.
Для решения задачи изображения трехмерного процесса на двухмерном дисплее с учетом положения наблюдателя употреблялись матрицы пересчета из мировых координат в видовые и из видовых – в оконные. Первая формируется функцией CreateViewCoords, а вторая – функцией SpaceToWindow. Определения функций представлены в приложении Е.
Задачи сохранения данных решены при помощи встроенных функций библиотек MFC при помощи дескрипторов устройств. Они употребляются в способе SaveImg (приложение Ж), вызываемом при успешном завершении диалога сохранения файла.
Построение поля, пересчет координат, поверхности октаэдр по настроенным параметрам возможно изобразить следующим образом:
| нет |
| Финиш |
| Расчет матриц пересчета из всемирный совокупности координат (МСК) в видовую и из видовой в оконную (ОСК) |
| Построение поля в МСК, пересчет координат, вывод на экран в ОСК |
| fi |
| q |
| Расчет требуемых шагов по вертикали (dq) и по горизонтали (df), перемещение МСК в центр пирамиды, расчет смещения октаэдра относительно начала мировых координат в ОСК |
| Начало |
| Выбрана диффузионная модель освещения |
| Расчет положения точки поверхности октаэдра в МСК, вычисление ее освещенности в зависимости от косинуса угла между падающим нормалью и лучом к поверхности в данной точке, установка пикселя соответствующего цвета в ОСК, q+=dq; |
| fi+=dfi; |
| да |
| да |
| нет |
| да |
| нет |
| Расчет требуемых шагов по вертикали (dq) и по горизонтали (df), перемещение МСК в центр пирамиды, расчет смещения октаэдра относительно начала мировых координат в ОСК |
| q |
| fi+=dfi; |
| fi |
| Расчет положения точки поверхности октаэдра в МСК, вычисление ее освещенности в зависимости от косинуса угла между направлением и отражённым лучом на наблюдателя в данной точке, установка пикселя соответствующего цвета в ОСК, q+=dq; |
| нет |
| нет |
| да |
| да |
Заключение
Созданное приложение моделирует заданный процесс перемещения октаэдра по плоскости с задаваемыми начальными параметрами перемещения. В будущем допустимо усовершенствование приложения методом применения аппаратных средств пересчета координат. Допустимо сохранение смоделированных изображений в графические файлы. Приобретены навыки применения на практике пакета MFC и математического аппарата аффинных преобразований.
Демонстрация работы приложения:
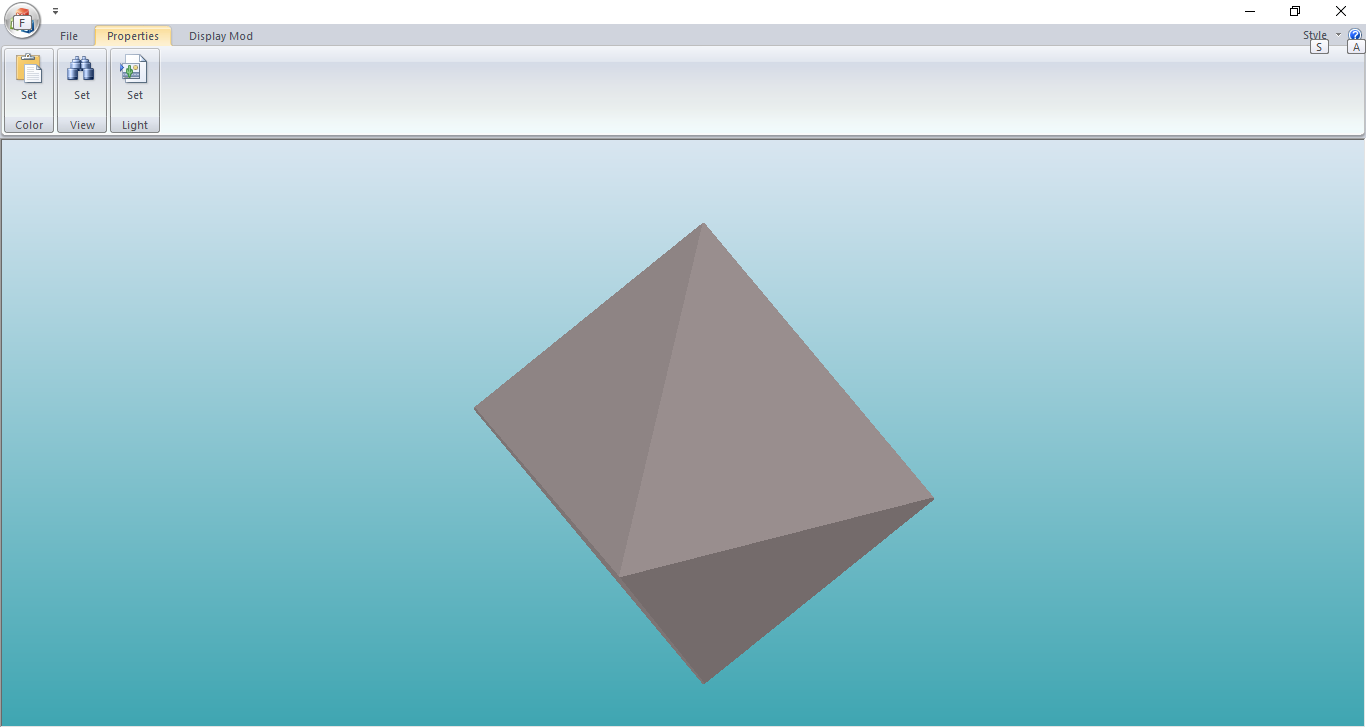
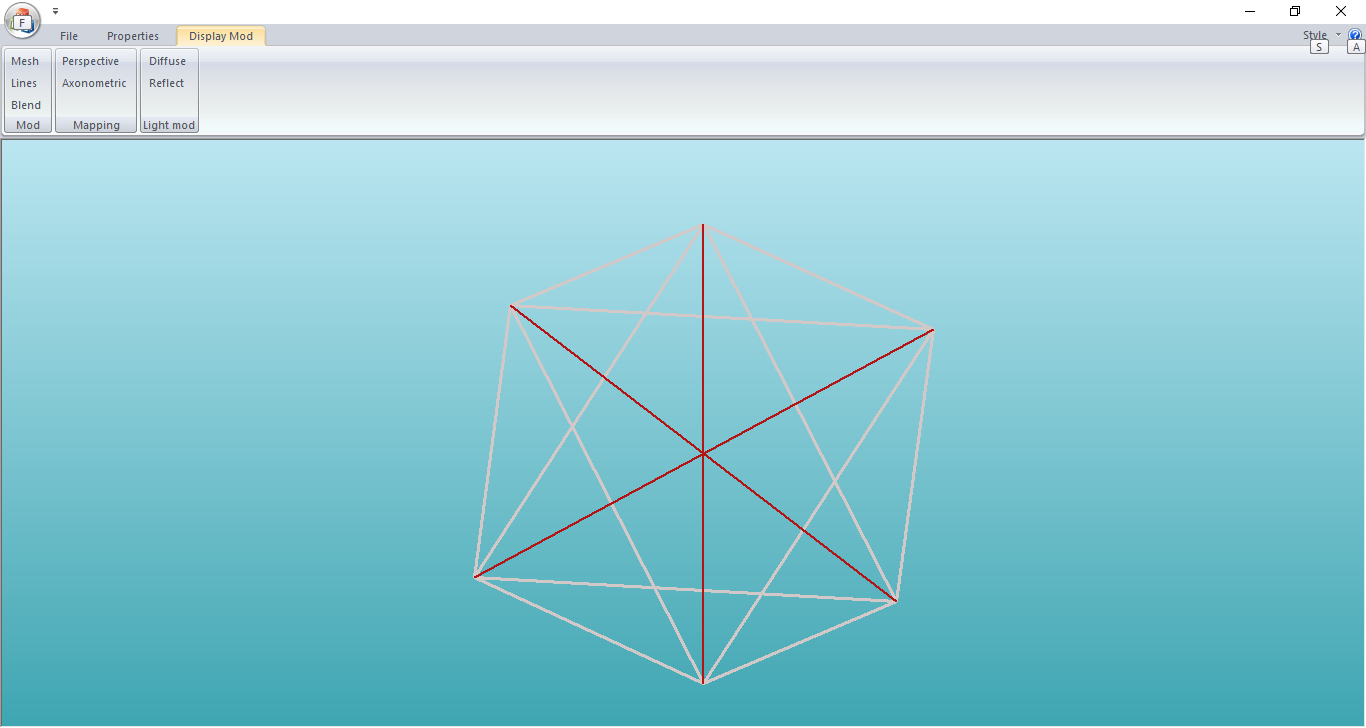
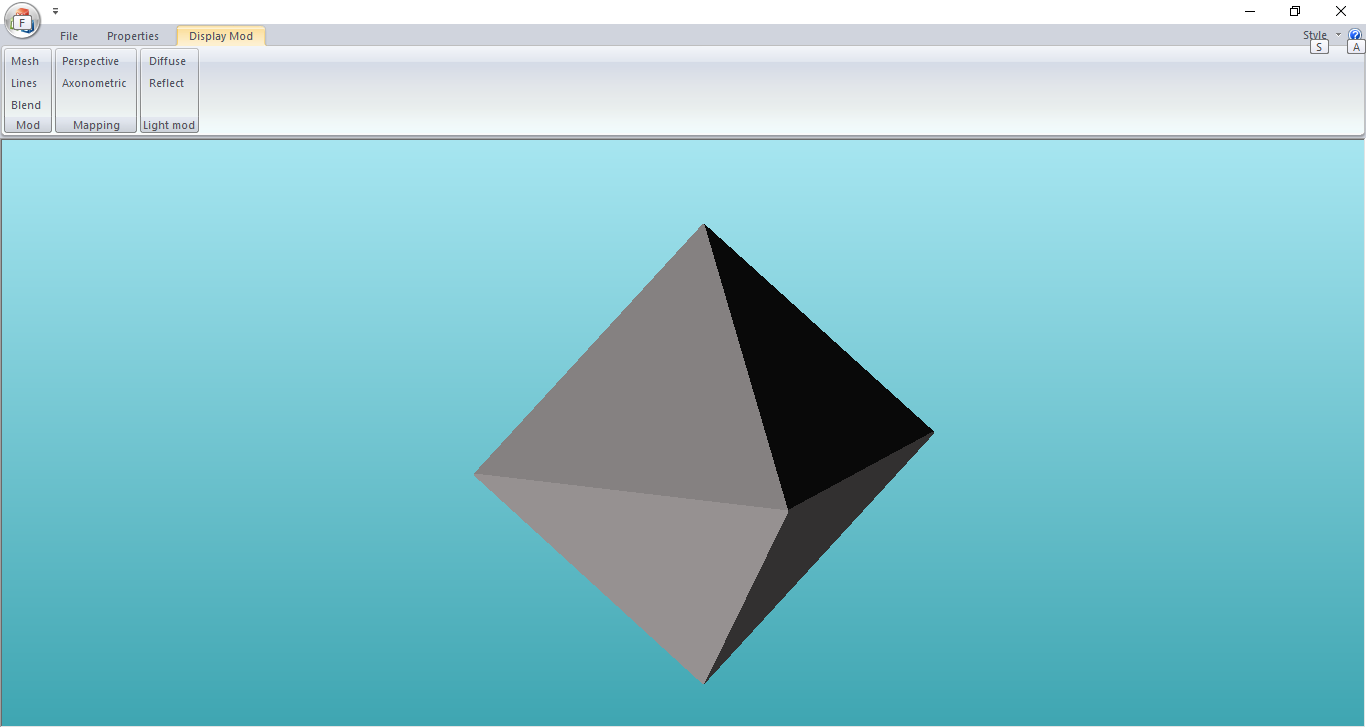
Рисунок 3 – Демонстрация работы приложения
Приложения
Приложение А. Структура CPyramid.
#include stdafx.h
class CPyramid
{
CMatrix Vertices; // Координаты вершин
CMatrix Vertices2; // Координаты вершин
void GetRect(CMatrix Vert,CRectD RectView);
public:
CPyramid();
void Draw(CDC dc,CMatrix P,CRect RW);
void Draw1(CDC dc,CMatrix P,CRect RW);
void ColorDraw(CDC dc,CMatrix PView,CRect RW,COLORREF Color, CMatrix PLight, int LightMode);
void ColorDrawD(CDC dc, CMatrix PView, CRect RW, COLORREF Color, CMatrix PLight);
void ColorDrawP(CDC dc, CMatrix PView, CRect RW, COLORREF Color, CMatrix PLight, int LightMode);
};
Приложение Б. Описание класса LibGraph.
#ifndef LIBGRAPH
#define LIBGRAPH 1
const double pi=3.14159;
//typedef double (*pfunc)(double); // Указатель на функцию
typedef double (*pfunc2)(double,double); // Указатель на функцию
struct CSizeD
{
double cx;
double cy;
};
//————————————————————————————
struct CRectD
{
double left;
double top;
double right;
double bottom;
CRectD(){left=top=right=bottom=0;};
CRectD(double l,double t,double r,double b);
void SetRectD(double l,double t,double r,double b);
CSizeD SizeD();
};
Приложение В. Описание класса CMatrix.
#include Math.h
#ifndef CMATRIXH
# define CMATRIXH 1
class CMatrix
{
double **array;
int n_rows; // Число строчков
int n_cols; // Число столбцов
public:
CMatrix(); // Конструктор по умолчанию (1 на 1)
CMatrix(int,int); // Конструктор
CMatrix(int); // Конструктор -вектора (один столбец)
CMatrix(const CMatrix); // Конструктор копирования
~CMatrix();
double operator()(int,int); // Выбор элемента матрицы по индексу
double operator()(int); // Выбор элемента вектора по индексу
CMatrix operator-(); // Оператор —
CMatrix operator=(const CMatrix); // Оператор Присвоить: M1=M2
CMatrix operator*(CMatrix); // Оператор Произведение: М1*М2
CMatrix operator*(double x); // Оператор Произведение: М1*a
CMatrix operator/(double x); // Оператор Деление: М1/a
CMatrix operator+(CMatrix); // Оператор +: M1+M2
CMatrix operator-(CMatrix); // Оператор -: M1-M2
CMatrix operator+(double); // Оператор +: M+a
CMatrix operator-(double); // Оператор -: M-a
int rows()const{return n_rows;} ; // Возвращает число строчков
int cols()const{return n_cols;}; // Возвращает число строчков
CMatrix Transp(); // Возвращает матрицу,транспонированную к текущей
CMatrix GetRow(int); // Возвращает строчок по номеру
CMatrix GetRow(int,int,int);
CMatrix GetCol(int); // Возвращает столбец по номеру
CMatrix GetCol(int,int,int);
CMatrix RedimMatrix(int,int); // Изменяет размер матрицы с уничтожением данных
CMatrix RedimData(int,int); // Изменяет размер матрицы с сохранением данных,
//каковые возможно сохранить
CMatrix RedimMatrix(int); // Изменяет размер матрицы с уничтожением данных
CMatrix RedimData(int); // Изменяет размер матрицы с сохранением данных,
//каковые возможно сохранить
double MaxElement(); // Большой элемент матрицы
double MinElement(); // Минимальный элемент матрицы
double Abs(); // Модуль матрицы
};
#endif
Приложение Г. Способы класса LibGraph.
#include stdafx.h
CRectD::CRectD(double l,double t,double r,double b)
{
left=l;
top=t;
right=r;
bottom=b;
}
//——————————————————————————
void CRectD::SetRectD(double l,double t,double r,double b)
{
left=l;
top=t;
right=r;
bottom=b;
}
//——————————————————————————
CSizeD CRectD::SizeD()
{
CSizeD cz;
cz.cx=fabs(right-left); // Ширина прямоугольной области
cz.cy=fabs(top-bottom); // Высота прямоугольной области
return cz;
}
//——————————————————————————
CMatrix SpaceToWindow(CRectD RS,CRect RW)
// Возвращает матрицу пересчета координат из мировых в оконные
// RS — область в мировых координатах — double
// RW — область в оконных координатах — int
{
CMatrix M(3,3);
CSize sz = RW.Size(); // Размер области в ОКНЕ
int dwx=sz.cx; // Ширина
int dwy=sz.cy; // Высота
CSizeD szd=RS.SizeD(); // Размер области в МИРОВЫХ координатах
double dsx=szd.cx; // Ширина в мировых координатах
double dsy=szd.cy; // Высота в мировых координатах
double kx=(double)dwx/dsx; // Масштаб по x
double ky=(double)dwy/dsy; // Масштаб по y
M(0,0)=kx; M(0,1)=0; M(0,2)=(double)RW.left-kx*RS.left; // Обновлено
M(1,0)=0; M(1,1)=-ky; M(1,2)=(double)RW.bottom+ky*RS.bottom; // Обновлено
M(2,0)=0; M(2,1)=0; M(2,2)=1;
return M;
}
//——————————————————————————
void SetMyMode(CDC dc,CRect RS,CRect RW) //MFC
// Устанавливает режим отображения MM_ANISOTROPIC и его параметры
// dc — ссылка на класс CDC MFC
// RS — область в мировых координатах — int
// RW — Область в оконных координатах — int
{
int dsx=RS.right-RS.left;
int dsy=RS.top-RS.bottom;
int xsL=RS.left;
int ysL=RS.bottom;
int dwx=RW.right-RW.left;
int dwy=RW.bottom-RW.top;
int xwL=RW.left;
int ywH=RW.bottom;
dc.SetMapMode(MM_ANISOTROPIC);
dc.SetWindowExt(dsx,dsy);
dc.SetViewportExt(dwx,-dwy);
dc.SetWindowOrg(xsL,ysL);
dc.SetViewportOrg(xwL,ywH);
}
//————————————————————————————
CMatrix CreateTranslate2D(double dx, double dy)
// Афинные преобразования
// Формирует матрицу для преобразования координат объекта при его смещении
// на dx по оси X и на dy по оси Y в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при смещении начала
// совокупности координат на -dx оси X и на -dy по оси Y при фиксированном положении объекта
{
CMatrix TM(3,3);
TM(0,0)=1; TM(0,2)=dx;
TM(1,1)=1; TM(1,2)=dy;
TM(2,2)=1;
return TM;
}
//————————————————————————————-
CMatrix CreateTranslate3D(double dx, double dy,double dz)
// Формирует матрицу для преобразования координат объекта при его смещении
// на dx по оси X, на dy по оси Y,на dz по оси Z в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при смещении начала
// совокупности координат на -dx оси X,на -dy по оси Y, на -dz по оси Z
// при фиксированном положении объекта
{
CMatrix TM(4,4);
for(int i=0;i
TM(0,3)=dx;
TM(1,3)=dy;
TM(2,3)=dz;
return TM;
}
//————————————————————————————
CMatrix CreateRotate2D(double fi)
// Формирует матрицу для преобразования координат объекта при его повороте
// на угол fi (при fi0 против часовой стрелки)в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при повороте начала
// совокупности координат на угол -fi при фиксированном положении объекта
// fi — угол в градусах
{
double fg=fmod(fi,360.0);
double ff=(fg/180.0)*pi; // Перевод в радианы
CMatrix RM(3,3);
RM(0,0)=cos(ff); RM(0,1)=-sin(ff);
RM(1,0)=sin(ff); RM(1,1)=cos(ff);
RM(2,2)=1;
return RM;
}
//———————————————————————————
CMatrix CreateRotate3DZ(double fi)
// Формирует матрицу для преобразования координат объекта при его повороте около оси Z
// на угол fi (при fi0 против часовой стрелки)в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при повороте начала
// совокупности координат около оси Z на угол -fi при фиксированном положении объекта
// fi — угол в градусах
{
double fg=fmod(fi,360.0);
double ff=(fg/180.0)*pi; // Перевод в радианы
CMatrix RM(4,4);
RM(0,0)=cos(ff); RM(0,1)=-sin(ff);
RM(1,0)=sin(ff); RM(1,1)=cos(ff);
RM(2,2)=1;
RM(3,3)=1;
return RM;
}
//———————————————————————————
CMatrix CreateRotate3DX(double fi)
// Формирует матрицу для преобразования координат объекта при его повороте около оси X
// на угол fi (при fi0 против часовой стрелки)в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при повороте начала
// совокупности координат около оси X на угол -fi при фиксированном положении объекта
// fi — угол в градусах
{
double fg=fmod(fi,360.0);
double ff=(fg/180.0)*pi; // Перевод в радианы
CMatrix RM(4,4);
RM(0,0)=1;
RM(1,1)=cos(ff); RM(1,2)=-sin(ff);
RM(2,1)=sin(ff); RM(2,2)=cos(ff);
RM(3,3)=1;
return RM;
}
//———————————————————————————
CMatrix CreateRotate3DY(double fi)
// Формирует матрицу для преобразования координат объекта при его повороте около оси Y
// на угол fi (при fi0 против часовой стрелки)в фиксированной совокупности координат
// — Либо —
// Формирует матрицу для преобразования координат объекта при повороте начала
// совокупности координат около оси Y на угол -fi при фиксированном положении объекта
// fi — угол в градусах
{
double fg=fmod(fi,360.0);
double ff=(fg/180.0)*pi; // Перевод в радианы
CMatrix RM(4,4);
RM(0,0)=cos(ff); RM(0,2)=sin(ff);
RM(1,1)=1;
RM(2,0)=-sin(ff); RM(2,2)=cos(ff);
RM(3,3)=1;
return RM;
}
//———————————————————————————
CMatrix VectorMult(CMatrix V1,CMatrix V2)
// Вычисляет векторное произведение векторов V1 и V2
{
int b1=(V1.cols()==1)(V1.rows()==3);
int b2=(V2.cols()==1)(V2.rows()==3);
int b=b1&&b2;
if(!b)
{
MessageBox(NULL,LVectorMult: неправильные размерности векторов! ,LОшибка,MB_ICONSTOP);
exit(1);
}
CMatrix W(3);
W(0)=V1(1)*V2(2)-V1(2)*V2(1);
//double x=W(0);
W(1)=-(V1(0)*V2(2)-V1(2)*V2(0));
//double y=W(1);
W(2)=V1(0)*V2(1)-V1(1)*V2(0);
//double z=W(2);
return W;
}
//——————————————————————————-
double ScalarMult(CMatrix V1,CMatrix V2)
// Вычисляет скалярное произведение векторов V1 и V2
{
int b1=(V1.cols()==1)(V1.rows()==3);
int b2=(V2.cols()==1)(V2.rows()==3);
int b=b1&&b2;
if(!b)
{
MessageBox(NULL,LScalarMult: неправильные размерности векторов! ,LОшибка,MB_ICONSTOP);
exit(1);
}
double p=V1(0)*V2(0)+V1(1)*V2(1)+V1(2)*V2(2);
return p;
}
//————————————————————————-
double ModVec(CMatrix V)
// Вычисляет модуль вектора V
{
int b=(V.cols()==1)(V.rows()==3);
if(!b)
{
MessageBox(NULL,LModVec: неправильнfz размерность вектора! ,LОшибка,MB_ICONSTOP);
exit(1);
}
double q=sqrt(V(0)*V(0)+V(1)*V(1)+V(2)*V(2));
return q;
}
//————————————————————————-
double CosV1V2(CMatrix V1,CMatrix V2)
// Вычисляет КОСИНУС угла между векторами V1 и V2
{
double modV1=ModVec(V1);
double modV2=ModVec(V2);
int b=(modV1
if(b)
{
MessageBox(NULL,LCosV1V2: модуль одного либо обоих векторов 1e-7!,LОшибка,MB_ICONSTOP);
exit(1);
}
int b1=(V1.cols()==1)(V1.rows()==3);
int b2=(V2.cols()==1)(V2.rows()==3);
b=b1&&b2;
if(!b)
{
MessageBox(NULL,LCosV1V2: неправильные размерности векторов! ,LОшибка,MB_ICONSTOP);
exit(1);
}
double cos_f=ScalarMult(V1,V2)/(modV1*modV2);
return cos_f;
}
//————————————————————————-
double AngleV1V2(CMatrix V1,CMatrix V2)
// Вычисляет угол между векторами V1 и V2 в градусах
{
double modV1=ModVec(V1);
double modV2=ModVec(V2);
int b=(modV1
if(!b)
{
MessageBox(NULL,LAngleV1V2: модуль одного либо обоих векторов 1e-7!,LОшибка,MB_ICONSTOP);
exit(1);
}
int b1=(V1.cols()==1)(V1.rows()==3);
int b2=(V2.cols()==1)(V2.rows()==3);
b=b1&&b2;
if(!b)
{
MessageBox(NULL,LAngleV1V2: неправильные размерности векторов! ,LОшибка,MB_ICONSTOP);
exit(1);
}
double cos_f=ScalarMult(V1,V2)/(modV1*modV2);
if(fabs(cos_f)1)
{
MessageBox(NULL,LAngleV1V2: модуль cos(f)1! ,LОшибка,MB_ICONSTOP);
exit(1);
}
double f;
if(cos_f0)f=acos(cos_f);
else f=pi-acos(cos_f);
double fg=(f/pi)*180;
return fg;
}
//———————————————————————————
CMatrix CreateViewCoord(double r,double fi,double q)
// Формирует матрицу пересчета точки из всемирный совокупности координат в видовую
// (r,fi,q)- координата ТОЧКИ НАБЛЮДЕНИЯ(начало видовой совокупности координат)
// во всемирной сферической совокупности координат( углы fi и q в градусах)
{
double fg=fmod(fi,360.0);
double ff=(fg/180.0)*pi; // Перевод в радианы
fg=fmod(q,360.0);
double qq=(fg/180.0)*pi; // Перевод в радианы
CMatrix VM(4,4);
VM(0,0)=-sin(ff); VM(0,1)=cos(ff);
VM(1,0)=-cos(qq)*cos(ff); VM(1,1)=-cos(qq)*sin(ff); VM(1,2)=sin(qq);
VM(2,0)=-sin(qq)*cos(ff); VM(2,1)=-sin(qq)*sin(ff); VM(2,2)=-cos(qq); VM(2,3)=r;
VM(3,3)=1;
return VM;
}
//————————————————————————————
CMatrix SphereToCart(CMatrix PView)
// Преобразует сферические координаты PView точки в декартовы
// PView(0) — r
// PView(1) — fi — азимут(отсчет от оси X), град.
// PView(2) — q — угол(отсчетот оси Z), град.
// Итог: R(0)- x, R(1)- y, R(2)- z
{
CMatrix R(3);
double r=PView(0);
double fi=PView(1); // Градусы
double q=PView(2); // Градусы
double fi_rad=(fi/180.0)*pi; // Перевод fi в радианы
double q_rad=(q/180.0)*pi; // Перевод q в радианы
R(0)=r*sin(q_rad)*cos(fi_rad); // x- координата точки наблюдения
R(1)=r*sin(q_rad)*sin(fi_rad); // y- координата точки наблюдения
R(2)=r*cos(q_rad); // z- координата точки наблюдения
return R;
}
//————————— GetProjection ——————————————-
void GetProjection(CRectD RS,CMatrix Data,CMatrix PView,CRectD PR)
// Вычисляет координаты проекции охватывающего фигуру паралелепипеда на
// плоскость XY в ВИДОВОЙ совокупности координат
// Data — матрица данных
// RS — область на плоскости XY, на которую опирается отображаемая поверхность
// PView — координаты точки наблюдения во всемирной сферической совокупности координат
// PR — проекция
{
double Zmax=Data.MaxElement();
double Zmin=Data.MinElement();
CMatrix PS(4,4); // Точки в мировом пространстве
PS(3,0)=1; PS(3,1)=1; PS(3,2)=1; PS(3,3)=1;
CMatrix MV=CreateViewCoord(PView(0),PView(1),PView(2)); //Матрица(4×4) пересчета
//в видовую совокупность координат
PS(0,0)=RS.left;
PS(1,0)=RS.top;
PS(2,0)=Zmax;
PS(0,1)=RS.left;
PS(1,1)=RS.bottom;
PS(2,1)=Zmax;
PS(0,2)=RS.right;
PS(1,2)=RS.top;
PS(2,2)=Zmax;
PS(0,3)=RS.right;
PS(1,3)=RS.bottom;
PS(2,3)=Zmax;
CMatrix Q=MV*PS; // Координаты верхней плоскости паралелепипеда в видовой СК
CMatrix V=Q.GetRow(0); // Строчок X — координат
double Xmin=V.MinElement();
double Xmax=V.MaxElement();
V=Q.GetRow(1); // Строчок Y — координат
double Ymax=V.MaxElement();
PS(2,0)=Zmin;
PS(2,1)=Zmin;
PS(2,2)=Zmin;
PS(2,3)=Zmin;
Q=MV*PS; // Координаты нижней плоскости паралелепипеда в видовой СК
V=Q.GetRow(1); // Строчок Y — координат
double Ymin=V.MinElement();
PR.SetRectD(Xmin,Ymax,Xmax,Ymin);
}
Приложение Д. Функции аффинных преобразований.
CMatrix Translate2D(double x,double y){ //смещение в двухмерной совокупности координат
CMatrix m(3,3);
m(0,0)=1;m(1,1)=1;m(2,2)=1;
m(0,2)=x;
m(1,2)=y;
return m;
}
CMatrix Rotate2D(double fi){ //поворот в двухмерной совокупности координат
CMatrix m(3,3);
double fi_r=fi*pi/180.0;
m(0,0)=cos(fi_r);
m(1,1)=cos(fi_r);
m(2,2)=1;
m(0,1)=-sin(fi_r);
m(1,0)=sin(fi_r);
return m;
}
//смещение в трехмерной совокупности координат
CMatrix Translate3D(double x,double y,double z){
CMatrix m(4,4);
m(0,0)=1;m(1,1)=1;m(2,2)=1;m(3,3)=1;
m(0,3)=x;
m(1,3)=y;
m(2,3)=z;
return m;
}
//поворот около оси ОZ
CMatrix Rotate3Dz(double fi){
CMatrix m(4,4);
double fi_r=fi*pi/180.0;
m(0,0)=cos(fi_r);
m(1,1)=cos(fi_r);
m(2,2)=1;m(3,3)=1;
m(0,1)=-sin(fi_r);
m(1,0)=sin(fi_r);
return m;
}
//поворот около оси ОХ
CMatrix Rotate3Dx(double fi){
CMatrix m(4,4);
double fi_r=fi*pi/180.0;
m(1,1)=cos(fi_r);
m(2,2)=cos(fi_r);
m(0,0)=1;m(3,3)=1;
m(1,2)=-sin(fi_r);
m(2,1)=sin(fi_r);
return m;
}
//поворот около оси ОY
CMatrix Rotate3Dy(double fi){
CMatrix m(4,4);
double fi_r=fi*pi/180.0;
m(0,0)=cos(fi_r);
m(2,2)=cos(fi_r);
m(1,1)=1;m(3,3)=1;
m(0,2)=-sin(fi_r);
m(2,0)=sin(fi_r);
return m;
}
Приложение Е. Функции преобразования координат.
//получение видовых координат по положению наблюдателя
CMatrix CreateViewCoord(double R,double fi,double theta){
CMatrix Ve(4,4),Mz(4,4);
Mz(0,0)=-1;Mz(1,1)=1;Mz(2,2)=1;Mz(3,3)=1;
double fi_r=fi*pi/180;
double theta_r=theta*pi/180;
Ve=Mz*Rotate3Dx(180-theta)*Rotate3Dz(90-fi);
return Ve;
}
//получение оконных координат по видовым
CMatrix SpaceToWindow(CRectD rs, CRect rw){
CMatrix m(3,3);
double kx=(rw.right-rw.left)/(rs.right-rs.left);
double ky=(rw.bottom-rw.top)/(rs.top-rs.bottom);
m(2,2)=1;
m(0,0)=kx;
m(1,1)=-ky;
m(0,2)=rw.left-kx*rs.left;
m(1,2)=rw.top-ky*rs.bottom;
return m;
}
Приложение Ж. Функция сохранения изображения в файл
//сохранение изображения окна hwnd в файл с путем-именем filename
char* SaveImg(HWND hwnd, char* filename)
{
BITMAPFILEHEADER bmfHdr; //файловый заголовок графического файла
BITMAPINFOHEADER bi; //информационный заголовок графического файла
RECT r;
int BitToPixel=24;
GetClientRect(hwnd,r); //получение клиентской области окна
HDC hdc=GetDC(hwnd); //получение исходного контекста окна
HDC hdcMem=CreateCompatibleDC(hdc); //создание совместимого контекста
HBITMAP BitMap=CreateCompatibleBitmap(hdc,r.right,r.bottom); //создание совместимой битовой карты
HBITMAP OldBitMap=(HBITMAP)SelectObject(hdcMem,BitMap); //совмещение битовой карты с контекстом
BitBlt(hdcMem,0,0,r.right,r.bottom,hdc,0,0,SRCCOPY); //копирование изображения из исходного контекста в совместимый
BitMap=(HBITMAP)SelectObject(hdcMem,OldBitMap);
ZeroMemory(bi,sizeof(BITMAPINFOHEADER));
//заполнение информационного заголовка
bi.biSize=sizeof(BITMAPINFOHEADER); //размер заголовка
bi.biWidth=r.right; //ширина изображения
bi.biHeight=r.bottom; //высота изображения
bi.biPlanes=1; //число слоев=1
bi.biBitCount=BitToPixel; //число битов/пиксель=24
bi.biSizeImage=(r.right*BitToPixel+31)/32*4*r.bottom; //размер изображения
DWORD dwWritten;
//получение дескриптора указанного файла
HANDLE fh=CreateFile(filename,GENERIC_WRITE,0,NULL,CREATE_ALWAYS,FILE_ATTRIBUTE_NORMAL|FILE_FLAG_SEQUENTIAL_SCAN,NULL);
//заполнение файлового заголовка
bmfHdr.bfType=(‘M’
bmfHdr.bfSize=bi.biSizeImage+sizeof(bmfHdr)+bi.biSize; //размер файла
bmfHdr.bfReserved1=bmfHdr.bfReserved2=0; //резервные биты
//отступ от начала файла до начала битов изображения=сумма длин заголовков
bmfHdr.bfOffBits=sizeof(bmfHdr)+bi.biSize;
//запись в файл файлового заголовка
WriteFile(fh,(LPSTR)bmfHdr,sizeof(bmfHdr),dwWritten,NULL);
//запись в файл информационного заголовка
WriteFile(fh,(LPSTR)bi,sizeof(bi),dwWritten,NULL);
//выделение памяти для битов изображения
char* lp=(char*)GlobalAlloc(GMEM_FIXED,bi.biSizeImage);
//получение аппаратно-свободного изображения
int err=GetDIBits(hdc,BitMap,0,(UINT)r.bottom,lp,(LPBITMAPINFO)bi,DIB_RGB_COLORS);
//запись изображения в файл
WriteFile(fh,lp,bi.biSizeImage,dwWritten,NULL);
//освобождение памяти, дескрипторов, контекстов.
GlobalFree(GlobalHandle(lp));
CloseHandle(fh);
ReleaseDC(hwnd,hdc);
DeleteDC(hdcMem);
return Готово!;
}
Перечень литературы
1. Поляков А., Брусенцев В. — алгоритмы и Методы компьютерной графики в примерах на Visual C++ — СПб.: БХВ-Петербург, 2003.
2. Давыдов В. — Visual C++. Создание Windows-приложений посредством MFC и API-функций.
3. Форум www.stackoverflow.com