Поиск ответов в задачах ИО.
Одна из главных задач ИО содержится в поиске таких ответов, каковые отвечают наилучшим (экстремальным) значениям выбранного критерия эффективности операции W .
Различают два нюанса управления: оптимизация, т.е. поиск ответов, доставляющих максимум либо минимум выбранному критерию, и ранжирование, т.е. упорядочение ответов в порядке убывания либо возрастания значений критерия. Задача ранжирования носит более личный темперамент, поскольку решается, в большинстве случаев, на ограниченном множестве ответов.
Как уже говорилось ранее, критерий эффективностиможет бытьскалярным, т.е. характеризоваться одним единственным числом, либо векторным, характеризующимся совокупностью чисел. Это зависит от характера решаемой задачи. К примеру, при управлении перехватчиком конечно в качестве критерия принять возможность поражения цели. В случае, если же перед нами стоит задача оценки проекта пассажирского лайнера, то нужно учитывать совокупность многих его особенностей: надежность, скорость, дальность, комфортабельность, рыночную конкурентоспособность и т.п.
В соответствии с характером выбранного критерия принято различать однокритериальныеимногокритериальныезадачи принятия ответов.
С учетом разнообразия задач управления, критерий эффективности W,в общем виде возможно записан следующим образом
W = Ф ( U, S, C ),
где:
Ф – некий функционал,
U — вектор управления . U= f(u1,u2,…un) ,i=1..n,
S — вектор, характеризующий окружающую среду,
C — вектор, характеризующий процесс ( совокупность).
Вектор С, со своей стороны, возможно представить в виде: С = Ф(К, Р), где вектор К={ki} характеризует структуру отечественной совокупности, а вектор P={pi} есть вектором параметров (конкретных числовых черт совокупности).
Данное выражение возможно разглядывать как математическую модель управляемого процесса (совокупности). C помощью данной модели возможно искать оптимальное управление , оптимальные параметры и оптимальную структуру при заданной структуре.
U0=arg max/min Ф (U,S,C) оптимизация управления .
u
K0= arg max/min Ф (U,S,C) оптимизацияструктуры .
k
P0= arg max/min Ф (U,S,C) параметрическая оптимизация.
p
Не снижая общности, зафиксируем значения факторов, действующих на протяжении операции, и опустим их обозначения при поиске оптимальных ответов, т.е. примем W = W(x), где xIX значение вектора управления – ответа, приятого оперирующей стороной.
В теории принятия ответов обширно употребителен термин «альтернатива». Этим термином обозначается каждое из несовместных вероятных ответов, определяемое в нашем случае значением вектора управления xIX.Каждойальтернативе будет соответствовать точка в критериальном пространстве. Совокупность всех ответов представляет собой полное множество альтернатив. Оно содержит как реализуемые, так и не реализуемые ответы. Понятие альтернативы комфортно тем, что оно обобщает все типы ответов независимо от их содержания. В нашем случае альтернативами являются как решения по выбору управления, так и решения по выбору структуры либо параметров управляемой совокупности. В рамках данной терминологии главная задача принятия ответов возможно сформулирована как задача поиска оптимальных альтернатив.
В общем случае W имеется векторный критерий — Wn={w1,w2…wn} .Его возможно разглядывать как n-мерный вектор, либо как точку в n- мерном пространстве, где w1, w2 … wn ее координаты. Образованное так пространство принято именовать критериальным, размерность его равна числу показателей (их довольно часто именуют локальными параметрами, в отличие от глобального векторного). Область всех вероятных значений векторного критерия, независимо от их реализуемости, образовывает, при двухсторонних ограничениях, гиперкуб, ребра которого отображают область вероятных значений соответствующих показателей wi.
Значительным недочётом векторного критерия есть то, что мы не можем решать оптимизационные задачи на его базе классическими регулярными способами, т.к. современный математический аппарат не располагает универсальным методом сопоставления векторов.
При скалярного критерия эффективности под наилучшим будем осознавать ответ, снабжающее большое значение показателя W. Тогда задача поиска наилучшего ответа возможно записана следующим образом:
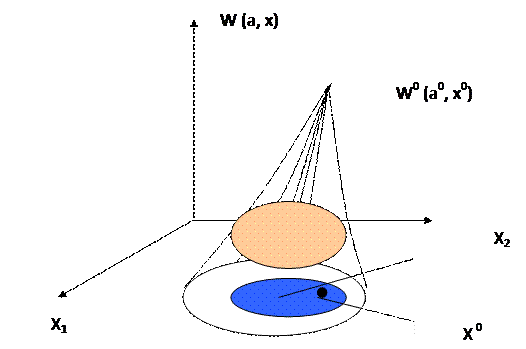
При заданном комплексе условий проведении операции, отыскать такое ответ x = x° (xIX),которое обращает показатель эффективности операции W в максимум, т.е.
W° (x°) = мах W(x)
xIX
(см. Рисунок)
 |
При минимизации показателя W, обуславливаемом его физическим смыслом (к примеру, затраты на создание совокупности), задача сводится к задаче максимизации трансформацией символа показателя W на противоположный.
В случае, если число вероятных вариантов ответа, образующих множество X мало, то для поиска оптимального ответа нужно, для каждого из вероятных значений xIX (решая прямую задачу) найти значение показателя W. Сравнив их между собой, возможно указать одно либо пара ответов, при которых W достигает максимума. Таковой метод именуется несложным перебором.
, если множество вероятных вариантов ответа X громадно, то поиск среди них оптимального несложным перебором не редкость очень затруднителен, а подчас легко неосуществим. С формальной точки зрения задача поиска оптимального ответа относятся к задаче математического программирования, где в качестве целевой функции употребляется критерий эффективности W(x). Термин программирование от британского programming – составление замысла либо программы действий, тут направляться осознавать в смысле “поиска наилучших замыслов — ответов”, а не в смысле разработки ПО для ЭВМ.
При векторного критерия эффективности под наилучшим (время от времени говорят рациональным) в большинстве случаев понимается ответ x = x° (xIX), снабжающее большое (минимальное) значение некоего обобщенного показателя U, что является результатом формализованной (неформализованной) свертки векторного критерия в скалярный
мax U = U(W(x)),
или ответ (одно из ответов) x = x° (xIX), отвечающее условию, что нельзя найти второе ответ, разрешающее улучшить любой из показателей Wi (i=1,к) не ухудшая наряду с этим значения вторых показателей Wx (x¹i) (хотя бы одно из них). Такие ответы именуются действенными либо паретовскими (xпIXп ).
Разглядим задачу поиска оптимальных (рациональных) ответов в общем случае (множество ответов возможно ограничено и не ограничено) более детально.
Пускай W векторный критерий — Wn={w1,w2…wn} .Его возможно разглядывать как точку в n- мерном пространстве, где w1, w2 … wn ее координаты.
Для решения задачи поиска оптимального ответа как скалярной применяют, как мы уже говорили, разные способы свертки вектора в скаляр. Разглядим кое-какие из них.
Критерий «взвешенной суммы»
B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами ai, каковые кроме этого именуются коэффициентами важности. Они отражают сокровище i-ого показателя (его важность для обобщенного показателя) если сравнивать с остальными.
Самый употребителен следующий вид свертки:
n
U =a ai ui
i=1
Тут ui -нормированное значение показателя wi, равное его отношению к размеру области вероятных значений. Чем ближе значение ui к 1, тем выше уровень качества, достигнутое по этому показателю. Нормировка вводится по причине того, что все слагаемые суммы должны иметь однообразную размерность, в противном случае их не было возможности бы складывать. В рассмотренном случае в качестве скаляризованного критерия употребляется среднее взвешенное значение показателей.
Для весовых коэффициентов так же вводится условие нормировки в виде: aai=1. Значения весовых коэффициентов ai назначаются специалистами либо ЛПР, или конкретно, или посредством особых процедур, каковые разрешают учесть разногласия между весами разных показателей.
Процедура яркого назначения специалистами либо ЛПР хороша тем, что она прозрачна и наилучшим образом отражает систему ценностей лица ее осуществляющего. Но она вероятна лишь, в случае, если размерность векторного критерия мала. В другом случае она может оказаться тяжело выполнимой.
В качестве особой процедуры назначения весовых коэффициентов довольно часто применяют так называемой “способ парных сравнений” (МПС).
В базу МПС положена квадратная матрица, строки и столбцы которой отвечают упорядоченным последовательностям показателей wi. Элементы матрицы аij показывают — на какое количество (для аддитивный свертки) либо во какое количество раз (для мультипликативной свертки) i-й показатель серьёзнее j – го и назначаются специалистами либо ЛПР для каждой пары показателей. При аддитивной свертке сумма весовых коэффициентов в каждой паре должна быть равна 1: (aij + aji = 1). При мультипликативной свертке произведение весовых коэффициентов в парах равняется 1: (aij * aji = 1).
Обработка заполненной матрицы дает возможность приобрести искомые нормированные коэффициенты важности ai.
При ярком назначении всех элементов матрицы парных сравнений специалисты либо ЛПР смогут показать непоследовательность суждений при сопоставлении отдельных пар, что приведет к нарушению элементов транзитивности и несогласованности матрицы соответствующих коэффициентов. В этом случае нужна коррекция сделанных назначений.
Но, матрицу возможно задать только первой строчком, и из нормировки и условий симметрии формально выяснить ее полностью.. Тогда она будет внутренне согласованной, но будет хуже отображать точку зрения ЛПР либо специалиста.
Необходимо заметить, что довольно часто в следствии свертки теряется содержательный суть взятого обобщенного критерия и обнаруженные его базе оптимальные ответы необходимо разбирать по достигнутому значению векторного критерия.
Также, потому, что выбор оптимального (рационального) ответа имеется прерогатива ЛПР и носит субъективный темперамент, исходя из этого выбор его параметров и метода свёртки нужно проводить, кроме этого, им конкретно (либо под его контролем).
ВЫБОР ГЛАВНОГО КРИТЕРИЯ
Относится к способам, не применяющим свертку векторного критерия в скалярный при поиске оптимального ответа.
Пускай (w1,w2,…,wn)- множество показателей. В соответствии с этим методом лицо, принимающее решения (ЛПР) выбирает самый ответственный показатель wi. Наряду с этим остальные показатели wj при j¹i переводятся в ограничения. Для задачи оптимизации возможно записать:
х 0=arg max wi (х) , при ограничениях: wj (х0) ³(?) cj при j¹i .
Данный метод по существу равносилен отказу от векторного критерия и переходу к скалярному. Наряду с этим происходит тяжелая потеря информации, т.к. значения всех параметров, не считая главного, учитываются лишь в ограничительном смысле.
СПОСОБ ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК.
В этом случае поиск ответа по векторному критерию реализовывают, оптимизируя решения поочередно по каждой компоненте векторного критерия, в порядке их предпочтения. Для этого показатели wi ранжируются по важности (предпочтительности). Но их упорядочение носит чисто качественный темперамент, т.е. никаких количественных оценок их важностей не производится. После этого выбирается первый, самый ответственный, показатель и находится оптимальная по нему альтернатива. Затем назначается уступка, т.е. промежуток, в котором смогут варьироваться значения первого показателя. Иначе говоря определяется — как первый показатель может различаться от собственного оптимального значения.
После этого производится оптимизация по второму показателю. Наряду с этим оптимальное значение второго показателя ищется при допустимой уступке первого. Потом определяется уступка по второму показателю и т.д. В качестве оптимальной по векторному критерию принимается альтернатива, вычисленная в конце многоэтапной оптимизации.
В этом способе скаляризация векторного критерия конкретно не производится. Возможность применения регулярных способов оптимизации обеспечивается за счет процедуры последовательного применения скалярных показателей (компонент wi) в качестве параметров оптимизации. От оптимизации по главному критерию данный метод принципиально отличается тем, что в ходе оптимизации участвуют все компоненты векторного критерия.
ПОИСК ОПТИМАЛЬНОГО Ответа
СПОСОБ «ВЗВЕШЕННОЙ СУММЫ»
B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами ai, каковые отражают сокровище i-ого показателя (его важность для обобщенного показателя) если сравнивать с остальными.
n
U =a ai ui
i=1
Весовые коэффициенты ai воображают в этом случае компоненты вектора градиента целевой функции. Поиск ответа сводится к задаче оптимизации с целевой функцией, линейной относительно компонент векторного критерия Wn(w1,w2…wn), но не вектора Х. Наилучшим будет ответ, расположенное максимально на большом растоянии в критериальном пространстве от начала координат в направлении градиента (см. рис.).
Необходимо заметить, что при применении способов, которые связаны с сопоставлением разных альтернатив по какой-либо компоненте векторного критерия понятие лучше (больше), в общем случае, не есть монотонной функцией собственного довода (напр. Температура воды для плавания в бассейне).
недостатки и Основные достоинства разных способов скаляризации векторного критерия.
Критерий среднего взвешенного. Преимущества
1. Простота формализации
2. Ясный физический суть
3. Учет личных представлений ЛПР о задаче при назначении весовых коэффициентов (важностей)
4. Наличие несложной формальной процедуры (способ парных сравнений), облегчающей процесс назначения весовых коэффициентов
Недочёты:
1. Неявная обоюдная компенсация показателей, которая делается неконтролируемой при солидном их числе.
Не учет нелинейной зависимости весовых коэффициентов от значений показателей: важности вводятся один раз и остаются постоянными размерами.
Способ совершенной точки. Преимущества:
1. Компоненты векторного критерия рассматриваются в совокупности (без применения сверток)
2. Четкая формальная постановка
Недочёты:
1. Неявная обоюдная компенсация показателей, которая делается неконтролируемой при солидном их числе.
2. Произвольный выбор метрики
3. Непредставимость, в содержательном смысле, расстояния между двумя точками в n-мерном пространстве (при n3).
Способ последовательных уступок. Преимущества:
1. Содержательная простота
2. Учет всех компонент векторного критерия
Недочёты:
1. Необходимость предварительного ранжирования показателей по важности
2 Трудность определения размеров уступок
3. Практическая не реализуемость при солидном числе показателей
Оптимальность по Парето. Преимущества:
1. Способ математически строг и понятен пользователю.
2. Выделяет множество допустимых ответов.,
3. Позволяет ЛПР сосредоточить анализ ответов на более узком множестве и выбрать субъективно оптимальное ответ.
Недочёты:
1. Применимость способа ограничена мощностью Парето-оптимального множества (для яркого выбора ответа количество его элементов не должно быть больше 7-10). В случае, если у недоминируемого множества громадная мощность, то способ тяжело выполним без привлечения одного из рассмотренных выше способов.
Свертка по полезности, свертка по предпочтениям.Не смотря на то, что оба способа возможно разглядывать как метод скаляризации векторного критерия, по существу это методы обнаружения неформальной информации, которой владеет ЛПР. Информации основанной на знаниях, опыте, интуиции и сложившейся на данной базе совокупности сокровищ ЛПР. Снаружи они несложны для пользователя, но это далеко не так. формализация и Выявление системы ценностей ЛПР, высказываемой в виде предпочтений либо полезностей требует организации достаточно сложных процедур. Одна из таких процедур будет рассмотрена ниже на примере СППР DSS/UTES. (см. лекции по ИО Бомас В.В.).
Поиск ответов в задачах ИО.
Одна из главных задач ИО содержится в поиске таких ответов, каковые отвечают наилучшим (экстремальным) значениям выбранного критерия эффективности операции W .
Различают два нюанса управления: оптимизация, т.е. поиск ответов, доставляющих максимум либо минимум выбранному критерию, и ранжирование, т.е. упорядочение ответов в порядке убывания либо возрастания значений критерия. Задача ранжирования носит более личный темперамент, поскольку решается, в большинстве случаев, на ограниченном множестве ответов.
Как уже говорилось ранее, критерий эффективностиможет бытьскалярным, т.е. характеризоваться одним единственным числом, либо векторным, характеризующимся совокупностью чисел. Это зависит от характера решаемой задачи. К примеру, при управлении перехватчиком конечно в качестве критерия принять возможность поражения цели. В случае, если же перед нами стоит задача оценки проекта пассажирского лайнера, то нужно учитывать совокупность многих его особенностей: надежность, скорость, дальность, комфортабельность, рыночную конкурентоспособность и т.п.
В соответствии с характером выбранного критерия принято различать однокритериальныеимногокритериальныезадачи принятия ответов.
С учетом разнообразия задач управления, критерий эффективности W,в общем виде возможно записан следующим образом
W = Ф ( U, S, C ),
где:
Ф – некий функционал,
U — вектор управления . U= f(u1,u2,…un) ,i=1..n,
S — вектор, характеризующий окружающую среду,
C — вектор, характеризующий процесс ( совокупность).
Вектор С, со своей стороны, возможно представить в виде: С = Ф(К, Р), где вектор К={ki} характеризует структуру отечественной совокупности, а вектор P={pi} есть вектором параметров (конкретных числовых черт совокупности).
Данное выражение возможно разглядывать как математическую модель управляемого процесса (совокупности). C помощью данной модели возможно искать оптимальное управление , оптимальные параметры и оптимальную структуру при заданной структуре.
U0=arg max/min Ф (U,S,C) оптимизация управления .
u
K0= arg max/min Ф (U,S,C) оптимизацияструктуры .
k
P0= arg max/min Ф (U,S,C) параметрическая оптимизация.
p
Не снижая общности, зафиксируем значения факторов, действующих на протяжении операции, и опустим их обозначения при поиске оптимальных ответов, т.е. примем W = W(x), где xIX значение вектора управления – ответа, приятого оперирующей стороной.
В теории принятия ответов обширно употребителен термин «альтернатива». Этим термином обозначается каждое из несовместных вероятных ответов, определяемое в нашем случае значением вектора управления xIX.Каждойальтернативе будет соответствовать точка в критериальном пространстве. Совокупность всех ответов представляет собой полное множество альтернатив. Оно содержит как реализуемые, так и не реализуемые ответы. Понятие альтернативы комфортно тем, что оно обобщает все типы ответов независимо от их содержания. В нашем случае альтернативами являются как решения по выбору управления, так и решения по выбору структуры либо параметров управляемой совокупности. В рамках данной терминологии главная задача принятия ответов возможно сформулирована как задача поиска оптимальных альтернатив.
В общем случае W имеется векторный критерий — Wn={w1,w2…wn} .Его возможно разглядывать как n-мерный вектор, либо как точку в n- мерном пространстве, где w1, w2 … wn ее координаты. Образованное так пространство принято именовать критериальным, размерность его равна числу показателей (их довольно часто именуют локальными параметрами, в отличие от глобального векторного). Область всех вероятных значений векторного критерия, независимо от их реализуемости, образовывает, при двухсторонних ограничениях, гиперкуб, ребра которого отображают область вероятных значений соответствующих показателей wi.
Значительным недочётом векторного критерия есть то, что мы не можем решать оптимизационные задачи на его базе классическими регулярными способами, т.к. современный математический аппарат не располагает универсальным методом сопоставления векторов.
При скалярного критерия эффективности под наилучшим будем осознавать ответ, снабжающее большое значение показателя W. Тогда задача поиска наилучшего ответа возможно записана следующим образом:
При заданном комплексе условий проведении операции, отыскать такое ответ x = x° (xIX),которое обращает показатель эффективности операции W в максимум, т.е.
W° (x°) = мах W(x)
xIX
(см. Рисунок)

 |
При минимизации показателя W, обуславливаемом его физическим смыслом (к примеру, затраты на создание совокупности), задача сводится к задаче максимизации трансформацией символа показателя W на противоположный.
В случае, если число вероятных вариантов ответа, образующих множество X мало, то для поиска оптимального ответа нужно, для каждого из вероятных значений xIX (решая прямую задачу) найти значение показателя W. Сравнив их между собой, возможно указать одно либо пара ответов, при которых W достигает максимума. Таковой метод именуется несложным перебором.
, если множество вероятных вариантов ответа X громадно, то поиск среди них оптимального несложным перебором не редкость очень затруднителен, а подчас легко неосуществим. С формальной точки зрения задача поиска оптимального ответа относятся к задаче математического программирования, где в качестве целевой функции употребляется критерий эффективности W(x). Термин программирование от британского programming – составление замысла либо программы действий, тут направляться осознавать в смысле “поиска наилучших замыслов — ответов”, а не в смысле разработки ПО для ЭВМ.
При векторного критерия эффективности под наилучшим (время от времени говорят рациональным) в большинстве случаев понимается ответ x = x° (xIX), снабжающее большое (минимальное) значение некоего обобщенного показателя U, что является результатом формализованной (неформализованной) свертки векторного критерия в скалярный
мax U = U(W(x)),
или ответ (одно из ответов) x = x° (xIX), отвечающее условию, что нельзя найти второе ответ, разрешающее улучшить любой из показателей Wi (i=1,к) не ухудшая наряду с этим значения вторых показателей Wx (x¹i) (хотя бы одно из них). Такие ответы именуются действенными либо паретовскими (xпIXп ).
Разглядим задачу поиска оптимальных (рациональных) ответов в общем случае (множество ответов возможно ограничено и не ограничено) более детально.
Пускай W векторный критерий — Wn={w1,w2…wn} .Его возможно разглядывать как точку в n- мерном пространстве, где w1, w2 … wn ее координаты.
Для решения задачи поиска оптимального ответа как скалярной применяют, как мы уже говорили, разные способы свертки вектора в скаляр. Разглядим кое-какие из них.
МЕТОДЫ СКАЛЯРИЗАЦИИ ВЕКТОРНОГО КРИТЕРИЯ
Существуют два подхода к скаляризации векторного критерия — формализованная и неформализованная свертка.
В первом случае (формализованная свертка) для получения обобщенного показателя (обозначим его как U) употребляется некое формальное выражение, разрешающее по заданному значению вектора Wn={w1,w2…wn}вычислить соответствующее ему значение обобщенного показателя
U=F (Wn)= F (w1,w2…wn), где Fнекоторая заданная функция.
Во втором случае (неформализованная свертка) разным значениям вектора Wn={w1,w2…wn}ставится в соответствиезначение обобщенного показателя без применения функциональных (формализованных) зависимостей. U=Y(Wn) = Y(w1,w2…wn).
В будущем, не снижая общности, будем обозначать сверткувекторного критерия в скаляр как U=U(Wn)=U(w1,w2…wn).
На практике самый употребительны два способа свертки показателей: аддитивная и мультипликативная.
В аддитивной свертке обобщенный показатель эффективности представляется в виде взвешенной суммы показателей.
В мультипликативной свертке обобщенный критерий воображаю в форме некоего произведения (отношения) показателей.
Разглядим эти методы свертки более детально.
Критерий «взвешенной суммы»
B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами ai, каковые кроме этого именуются коэффициентами важности. Они отражают сокровище i-ого показателя (его важность для обобщенного показателя) если сравнивать с остальными.
Самый употребителен следующий вид свертки:
n
U =a ai ui
i=1
Тут ui -нормированное значение показателя wi, равное его отношению к размеру области вероятных значений. Чем ближе значение ui к 1, тем выше уровень качества, достигнутое по этому показателю. Нормировка вводится по причине того, что все слагаемые суммы должны иметь однообразную размерность, в противном случае их не было возможности бы складывать. В рассмотренном случае в качестве скаляризованного критерия употребляется среднее взвешенное значение показателей.
Для весовых коэффициентов так же вводится условие нормировки в виде: aai=1. Значения весовых коэффициентов ai назначаются специалистами либо ЛПР, или конкретно, или посредством особых процедур, каковые разрешают учесть разногласия между весами разных показателей.
Процедура яркого назначения специалистами либо ЛПР хороша тем, что она прозрачна и наилучшим образом отражает систему ценностей лица ее осуществляющего. Но она вероятна лишь, в случае, если размерность векторного критерия мала. В другом случае она может оказаться тяжело выполнимой.
В качестве особой процедуры назначения весовых коэффициентов довольно часто применяют так называемой “способ парных сравнений” (МПС).
В базу МПС положена квадратная матрица, строки и столбцы которой отвечают упорядоченным последовательностям показателей wi. Элементы матрицы аij показывают — на какое количество (для аддитивный свертки) либо во какое количество раз (для мультипликативной свертки) i-й показатель ответственнее j – го и назначаются специалистами либо ЛПР для каждой пары показателей. При аддитивной свертке сумма весовых коэффициентов в каждой паре должна быть равна 1: (aij + aji = 1). При мультипликативной свертке произведение весовых коэффициентов в парах равняется 1: (aij * aji = 1).
Обработка заполненной матрицы дает возможность приобрести искомые нормированные коэффициенты важности ai.
При ярком назначении всех элементов матрицы парных сравнений специалисты либо ЛПР смогут показать непоследовательность суждений при сопоставлении отдельных пар, что приведет к нарушению элементов транзитивности и несогласованности матрицы соответствующих коэффициентов. В этом случае нужна коррекция сделанных назначений.
Но, матрицу возможно задать только первой строчком, и из нормировки и условий симметрии формально выяснить ее полностью.. Тогда она будет внутренне согласованной, но будет хуже отображать точку зрения ЛПР либо специалиста.