Говорят, что квадратная матрица с элементами из поля приводится к диагональному виду над , в случае, если существует невырожденная квадратная матрица с элементами из такая, что матрица – диагональная.
Теорема 15.8 (критерий приводимости квадратной матрицы к диагональному виду). Чтобы квадратная матрица n-го порядка приводилась к диагональному виду над полем нужно и достаточно, дабы все корни ее характеристического уравнения принадлежали этому полю и для каждого из них выполнялось условие
, (15.17)
где – кратность корня характеристического уравнения матрицы .
В том случае, в то время, когда все характеристические числа матрицы разны и принадлежат полю , эта матрица приводится к диагональному виду над . В случае, если приводится к диагональному виду – матрице , то диагональными элементами последней являются личные значения матрицы , а матрица , приводящая к диагональному виду, имеется не что иное, как матрица перехода от исходного базиса к базису из собственных векторов.
Правило приведения квадратной матрицы к диагональному виду над полем Р. 1. Составляем характеристический многочлен матрицы и находим его корни. В случае, если какой-либо из них не в собственности полю Р, то к диагональному виду не приводится.
2.В случае, если все корни характеристического уравнения принадлежат полю , то для кратных корней контролируем условие (15.17) (для однократных оно выполняется в любой момент). В случае, если для какого-либо из корней условие (15.17) не выполняется, то к диагональному виду не приводится.
3. В случае, если для каждого из собственных значений условие (15.17) выполняется, то к диагональному виду приводится. Записываем данный диагональный вид – матрицу , располагая на ее основной диагонали личные значения в произвольном порядке, причем каждое из значений повторяется столько раз, какова его кратность.
4. Для каждого из отысканных собственных значений находим предельное число линейно свободных собственных векторов и составляем из них базис, причем порядок векторов в базисе определяется матрицей : -й вектор базиса –это личный вектор, соответствующий собственному значению, расположенному на -м месте диагонали матрицы .
5) Составляем матрицу , приводящую к диагональному виду, – матрицу перехода от исходного базиса к выстроенному базису из собственных векторов. Для этого в столбцы матрицы записываем координатные столбцы соответствующих векторов выстроенного базиса. Необходимо заметить, что матрица находится неоднозначно.
Пример 15.35. Проверить, приводится ли матрица к диагональному виду. В случае, если приводится, отыскать данный диагональный вид и невырожденную матрицу , приводящую нему.
.
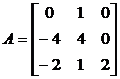Составляем и решаем характеристическое уравнение:
.
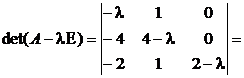Матрица имеет лишь одно собственное значение , но его кратность равна трем. Контролируем исполнение условия (15.17):
.
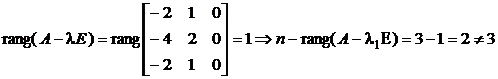Условие не выполняется, значит, матрица к диагональному виду не приводится.
Необходимо заметить, в случае, если кратность собственного значения не диагональной матрицы сходится с ее порядком, то она к диагональному виду не приводится.
Пример 15.36. Проверить, приводится ли матрица к диагональному виду. В случае, если приводится, отыскать данный диагональный вид и невырожденную матрицу , приводящую нему.
.
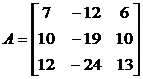Ответ снова проводим по намеченному замыслу.
1. 
–
.
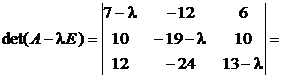
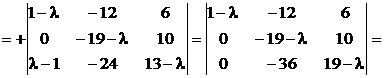
2. Контролируем исполнение условия (8.20) для кратного корня :
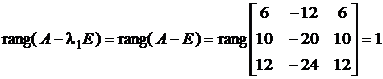. (15.18)
Так, , условие выполняется, матрица к диагональному виду приводится.
3. 
.
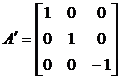4. Так как , то , т. е для первого собственного значения возможно отыскать два линейно свободных собственных вектора. По одной из строчков матрицы (15.18), поделив все ее элементы на неспециализированный множитель, выписываем единственное линейно свободное уравнение для отыскания координат собственных векторов и решаем его: . В качестве двух линейно свободных ответов возможно забрать, к примеру, следующие: , (фундаментальную совокупность ответов). Для второго собственного значения личный вектор находим, применяя алгебраические дополнения к элементам третьей строки матрицы, предварительно поделив все ее строки на неспециализированный множитель, что решения совокупности не изменяет.
: 
; , .
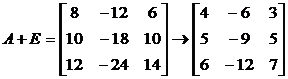5. 
.
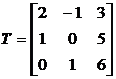Пример 15.37. Проверить, приводится ли матрица к диагональному виду а) над полем настоящих чисел; б) над полем комплексных чисел. В случае, если приводится, отыскать данный диагональный вид и невырожденную матрицу Т, приводящую нему.
.
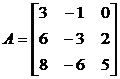1. 
; .
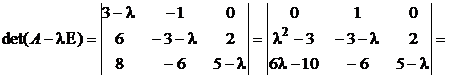
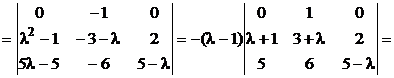
2. а) Так как характеристический многочлен имеет комплексные корни, то над полем настоящих чисел матрица к диагональному виду не приводится.
б) Над полем комплексных чисел матрица к диагональному виду приводится, поскольку все корни однократны.
3. 
.
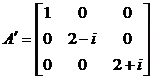4. Для первого и второго собственных значений при ответе совокупности используем алгебраические дополнения к элементам третьей строки:
: 
; , ;
: 
; , .
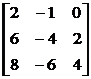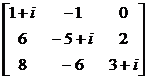Третий личный вектор находим как комплексно сопряженный второму: .
5. 
.
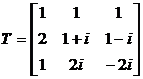Пример 15.38. Проверить, приводится ли матрица к диагональному виду над полем комплексных чисел. В случае, если приводится, отыскать данный диагональный вид и невырожденную матрицу , приводящую нему.
.
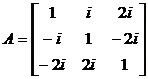1.
; .
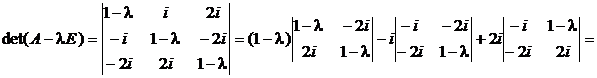2.Все корни однократны, исходя из этого матрица приводится к диагональному виду.
3. 
.
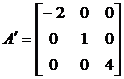4. Все личные векторы будем искать посредством алгебраических дополнений к элементам первой строки.
: 
; = ;
: 
; , ;
: 
; = .
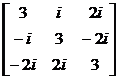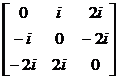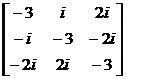5. 
.
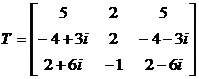Замечание. Обратите внимание на следующий интересный факт: в примере 15.37 исходная матрица настоящая, а ее диагональный вид – матрица комплексная, а в примере 15.38 напротив: исходная матрица комплексная, а ее диагональный вид – настоящая. Попытайтесь обосновать данный факт теоретически.
Присоединенные векторы
В случае, если – собственное значение линейного оператора , а совокупность векторов пространства удовлетворяет условиям:
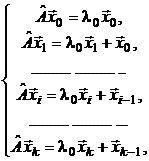
то вектор , именуется i-мприсоединенным вектором к собственному вектору линейного оператора .
Теорема 15.9. Пускай – линейное пространство над полем . В случае, если все характеристические числа линейного оператора принадлежат полю , то в существует базис, складывающийся из собственных и присоединенных векторов оператора , причем каждому собственному значению в этом базисе соответствует столько собственных векторов и присоединенных к ним, какова кратность этого собственного значения.
Выберем в пространстве какой-либо базис и обозначим матрицу линейного оператора в этом базисе, – координатные столбцы векторов соответственно в том же базисе. Для нахождения присоединенных векторов направляться решить совокупность линейных уравнений
. (15.19)
Так, приобретаем следующее
Правило нахождения присоединенных векторов. 1.Находим личные значения матрицы , решая ее характеристическое уравнение.
2. Для всех собственных значений находим личные векторы , решая однородную совокупность . Число линейно свободных собственных векторов с собственным значением равняется , где – размерность линейного пространства (либо порядок матрицы ). В случае, если собственное значение имеет кратность , то общее число присоединенных векторов, соответствующих всем собственным векторам с этим собственным значением, равняется .
3. Для каждого из отысканных собственных векторов находим присоединенные к ним (если они существуют). Из (15.19) видно, что для отыскания i-го присоединенного вектора к собственному вектору с собственным значением направляться решить совокупность линейных уравнений с той же матрицей, что и для отыскания собственного вектора , но неоднородную, причем в качестве столбца свободных участников для отыскания первого присоединенного берется координатный столбец соответствующего собственного вектора, а для всех последующих – координатный столбец прошлого присоединенного вектора.
Пример 15.39. Отыскать базис из собственных и присоединенных векторов линейного оператора , матрица которого в некоем базисе сходится с матрицей .
.
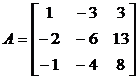? Решаем задачу по замыслу, приведенному в начале параграфа.
1. Ищем личные значения:
.
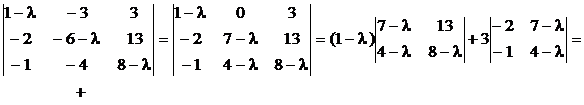
Характеристическое уравнение имеет единственный корень , кратность которого равна 3.
2. Определяем количество собственных и присоединенных векторов:
,
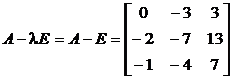. Значит, в искомом базисе – один личный вектор и два присоединенных к нему. Находим личный вектор, решая однородную совокупность с матрицей .
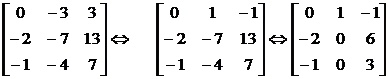. (15.20)
Приобретаем совокупность:
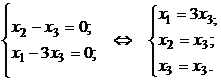
В качестве собственного вектора возможно забрать, к примеру, частное ответ .
3. Находим первый присоединенный вектор, дописывая в цепочке (15.20) к матрице в качестве столбца свободных участников координатный столбец отысканного собственного вектора и пересчитывая столбец свободных участников (лишь данный столбец!) по намеченным стрелкам:
.
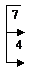
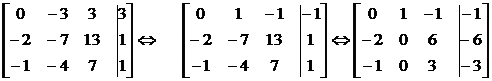Приобретаем совокупность
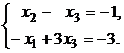(15.21)
Первый присоединенный вектор находим как частное ответ совокупности (15.21): . Дабы отыскать второй, дописываем к цепочке (15.20) еще и координатный столбец вектора в качестве столбца свободных участников и пересчитываем его по намеченным стрелкам (снова же лишь данный столбец):
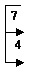
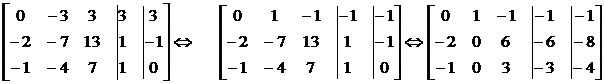по взятой матрице выписываем совокупность, не обращая внимания на прошлый столбец свободных участников:
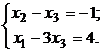(15.22)
Частное ответ совокупности (15.22) и будет вторым присоединенным вектором: .
Итак, искомый базис: – личный; – 1-й присоединенный; – 2-й присоединенный векторы. ^
Замечания. 1. В этом случае личный вектор возможно отыскать и при помощи алгебраических дополнений. Но это невыгодно, поскольку все равно нужно будет решать совокупность для отыскания присоединенных векторов.
2. На практике все три цепочки объединяются в одну, новый столбец свободных участников дописывается к матрице прошлой совокупности и пересчитывается по намеченным стрелкам. Само собой разумеется, возможно каждую из совокупностей решать раздельно, но приведенный способ разрешает проводить вычисления значительно стремительнее.
3.Приведенный способ ответа совокупностей разрешает скоро найти допущенную неточность: при верном ответе во всех совокупностях пропорциональными выясняются одинаковые строки.
4. Искомый базис строится неоднозначно. Если вы нашли какой-то личный вектор, то любой коллинеарный ему кроме этого будет собственным с тем же самым собственным значением. Для присоединенных векторов это утверждение неверно. В случае, если вас по каким-либо обстоятельствам отысканный присоединенный вектор не устаивает (к примеру, имеет дробные координаты), то поменять его вы имеете возможность, лишь придав свободным малоизвестным другие значения.
Пример 15.40. Отыскать базис из собственных и присоединенных векторов линейного оператора , матрица которого в некоем базисе сходится с матрицей , в случае, если
.
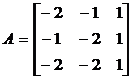? Ищем личные значения:
| – |
| + |
.
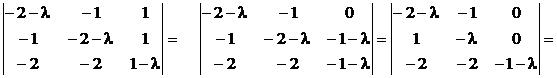
Находим личные векторы:
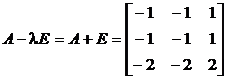(15.23)
, , значит, в искомом базисе два собственных вектора и у одного из них имеется присоединенный. Неспециализированное ответ однородной совокупности с матрицей (15.23): . Придавая свободным малоизвестным значения, как в большинстве случаев, по строчкам единичной матрицы, приобретаем два линейно свободных собственных вектора и . В случае, если выбрать в качестве столбца свободных участников координатный столбец одного из отысканных собственных векторов, возьмём совокупность с расширенной матрицей
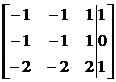либо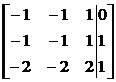 
.
Разумеется, обе эти совокупности несовместны. Это показывает, что мы неправильно выбрали личные векторы. В разглядываемом случае оказалась целая плоскость собственных векторов, а присоединенные имеется лишь у векторов одного направления. Дабы выбрать подходящий личный вектор, в качестве столбца свободных участников берем неспециализированное ответ однородной совокупности:
.
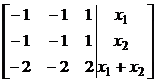Свободным малоизвестным подбираем такие значения, дабы оказалась совместная неоднородная совокупность, к примеру, . В этом случае первым вектором в базисе будет личный , для отыскания присоединенного к нему из последней совокупности приобретаем уравнение , одним из частных ответов которого будет (присоединенный вектор). Третьим вектором в искомом базисе направляться забрать еще один личный вектор, т.е. еще одно частное ответ однородной совокупности. Дабы обеспечивать линейную независимость векторам и , в общем ответе совокупности свободным малоизвестным направляться придать значения по строчкам любой невырожденной матрицы. Для нахождения мы уже применяли строчок , вторая строчок выбирается произвольно, только бы матрица оказалась невырожденная. Заберём, например, строчок . Тогда .
Итак, искомый базис: – личный; – присоединенный к нему; – личный. ^ 