Приложение i. значения функции нормального распределения с параметрами 0 и 1 (для отрицательных значений z) 2 глава

Ответ

Введите в диапазон A1:E1 страницы 1 рабочей книги Excel: в ячейку A1 заголовок «№ п/п», в ячейку B1 – заголовок «Cu», в ячейку C1 – заголовок «Pb», в ячейку D1 – заголовок «Zn», в ячейку E1 – заголовок «Au». Для исполнения корреляционного анализа введите в диапазон A2:E51 введите данные из табл. VI.1 по столбцам: A – № п/п, B – Cu, %, C – Pb, %, D – Zn, %, E – Au, г/т.

После этого в меню Сервис выберите пункт Анализ данных и потом укажите строчок Корреляция. В показавшемся диалоговом окне укажите Входной промежуток В1:E51. Укажите, что эти рассматриваются по столбцам. Установите флажок в поле Метки в первой строке. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервали в правое поле ввода Выходной промежуток введите G2. Надавите кнопку OK.

Результаты анализа. В выходном диапазоне приобретаем корреляционную матрицу.

Интерпретация результатов. Из таблицы видно, что корреляция между содержанием Cu и Au – 0,28 – линейную связь между содержанием золота и меди распознать не удалось, Pb и Au – 0,49 – возможно сказать о наличии корреляционной связи между свинцом и золотом, Zn и Au – 0,545 – возможно сказать о наличии корреляционной связи между цинком и золотом. Коэффициент парной корреляции между Zn и Pb, равный 0,572 говорит о том, что возможно сказать кроме этого о наличии корреляционной связи между свинцом и цинком.

Подразумевается, что в безлюдных клетках в правой верхней половине таблицы находятся те же коэффициенты корреляции, что и в нижней левой (симметрично расположенные относительно диагонали).

Введите в диапазон A1:E1 страницы 2 рабочей книги Excel: в ячейку A1 заголовок «№ п/п», в ячейку B1 – заголовок «Cu», в ячейку C1 – заголовок «Pb», в ячейку D1 – заголовок «Zn», в ячейку E1 – заголовок «Au». Для продолжения корреляционного анализа введите в диапазон A2:E51 страницы 2 рабочей книги Excel данные из табл. VI.2 по столбцам: A – № п/п, B – Cu, %, C – Pb, %, D – Zn, %, E – Ag, г/т. Подобно получите корреляционную матрицу.

Интерпретация результатов. Из таблицы видно, что корреляция между содержанием Cu и Ag – 0,48 – возможно сказать о наличии корреляционной связи между содержанием серебра и меди, Pb и Ag – 0,62 – возможно сказать о наличии линейной корреляционной связи между серебром и свинцом, Zn и Ag – 0,675 – возможно сказать о наличии линейной корреляционной связи между серебром и цинком. Коэффициент парной корреляции между Zn и Pb, равный 0,572 говорит о том, что возможно сказать кроме этого о наличии корреляционной связи между свинцом и цинком.

Введите в диапазон A1:E1 страницы 3 рабочей книги Excel: в ячейку A1 заголовок «№ п/п», в ячейку B1 – заголовок «Cu», в ячейку C1 – заголовок «Pb», в ячейку D1 – заголовок «Zn», в ячейку E1 – заголовок «Au». Потом введите в диапазон A2:E51 страницы 3 рабочей книги Excel данные из табл. VI.3 по столбцам: A – № п/п, B – Cu, %, C – Pb, %, D – Zn, %, E – Cd, 10-4 %. Получите корреляционную матрицу.

Интерпретация результатов. Из таблицы видно, что корреляция между содержанием Cu и Cd – 0,64 – возможно сказать о наличии линейной корреляционной связи между содержанием кадмия и меди, Pb и Cd – 0,48 – возможно сказать о наличии корреляционной связи между кадмием и свинцом, Zn и Cd – 0,981 – между параметрами существует фактически линейная зависимость между кадмием и цинком. Коэффициент парной корреляции между Zn и Cu, равный 0,628 говорит о том, что возможно сказать кроме этого о наличии линейной корреляционной связи между медью и цинком.

Введите в диапазон A1:E1 страницы 4 рабочей книги Excel: в ячейку A1 заголовок «№ п/п», в ячейку B1 – заголовок «Cu», в ячейку C1 – заголовок «Pb», в ячейку D1 – заголовок «Zn», в ячейку E1 – заголовок «Au». Введите в диапазон A2:E51 страницы 4 рабочей книги Excel данные из табл. VI.4 по столбцам: A – № п/п, B – Cu, %, C – Pb, %, D – Zn, %, E – Sb, 10-4 %. Получите корреляционную матрицу.

Интерпретация результатов. Из таблицы видно, что корреляция между содержанием Cu и Sb – 0,49 – возможно сказать о наличии корреляционной связи между содержанием сурьмы и меди, Pb и Sb – 0,60 – возможно сказать о наличии линейной корреляционной связи между сурьмой и свинцом, Zn и Sb – 0,944 – возможно сказать о наличии сильной линейной корреляционной связи между сурьмой и цинком. Коэффициент парной корреляции между Zn и Pb, равный 0,572 говорит о том, что возможно сказать кроме этого о наличии корреляционной связи между свинцом и цинком.

Введите в диапазон A1:E1 страницы 5 рабочей книги Excel: в ячейку A1 заголовок «№ п/п», в ячейку B1 – заголовок «Cu», в ячейку C1 – заголовок «Pb», в ячейку D1 – заголовок «Zn», в ячейку E1 – заголовок «Au». Введите в диапазон A2:E51 страницы 5 рабочей книги Excel данные из табл. VI.5 по столбцам: A – № п/п, B – Cu, %, C – Pb, %, D – Zn, %, E – Ba, %. Получите корреляционную матрицу.

Интерпретация результатов. Из таблицы видно, что корреляция между содержанием Cu и Ba – 0,10 – возможно сказать о том, что корреляционную связь между содержанием бария и меди распознать не удалось, Pb и Ba – 0,74 – возможно сказать о наличии линейной корреляционной связи между барием и свинцом, Zn и Ba – 0,41 – возможно сказать о наличии корреляционной связи между барием и цинком. Коэффициент парной корреляции между Zn и Pb, равный 0,572 говорит о том, что возможно сказать кроме этого о наличии корреляционной связи между свинцом и цинком.

МНОЖЕСТВЕННАЯ ЕЕ ИСПОЛЬЗОВАНИЕ и Регрессия ДЛЯ ПРЕДСКАЗАНИЯ ОСОБЕННОСТЕЙ ГЕОЛОГИЧЕСКИХ ОБЪЕКТОВ

В отличие от двумерной регрессии в способах множественной регрессии зависимая переменная Y рассматривается как функция не одной, а нескольких свободных переменных X1, X2 , …, Xm.

Уравнение множественной регрессии зависимой переменной Y довольно т свободных переменных X1,2,…,m записывается как линеаризированная функция вида

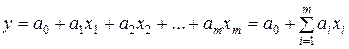, (VI.1)

где a0, a1, a2, …, am – требующие определения коэффициенты регрессии. Оно наилучшим методом (в смысле мельчайших квадратов) обрисовывает тенденцию размещения наблюденных точек в m-мерном пространстве и разрешает оценить совместное влияние всех изучаемых параметров на зависимую переменную.

Множественная регрессия строится на базе учета всех вероятных сотрудничеств между переменными и их сочетаниями. В ее задачи входит оценка неспециализированного вклада всех переменных (R2) в изменчивость Y, и определение относительного влияния каждой из них посредством коэффициентов ai,. Так, множественный регрессионный анализ сводится к вычислению значений коэффициентов регрессионной модели a0, a1, a2, …, am по совокупности п наблюдений над переменными X1, X2 , …, Xm и Y, оценке влияния каждой переменной и их неспециализированного вклада в оценку зависимой переменной Y. В матричной форме уравнение (VI.1) записывается как:

[?Y] = [?X] [a],

где [?Y] – вектор-столбец, складывающийся из смешанных произведений и сумм квадратов переменной Y с переменными X1, X2 , …, Xm;[?X] – матрица смешанных произведений и сумм квадратов X1, X2 , …, Xm; [a] – вектор-столбец малоизвестных коэффициентов регрессии. Коэффициенты регрессии ai рассчитываются как частные коэффициенты регрессии, характеризующие трансформации данной свободной переменной при условии, что влияние всех остальных переменных устранено.

Для сравнительной оценки вклада каждой зависимой переменной коэффициент R2 сперва рассчитывается для пары Y и Xk с большим коэффициентом корреляции, а после этого последовательно с тремя и более переменными (до т переменных).

Модели множественной регрессии употребляются для предсказаний значений зависимой переменной (к примеру, содержаний полезного элемента, глубины массы формирования и объёмной руды минерала и др.) по комплекту свободных переменных (к примеру, содержаний породообразующих элементов, объемных весов тяжелых минералов в рудах, содержаний элементов-индикаторов в минералах и др.).

ПРИМЕР VI.2

Требуется

Применяя результаты прошлого ПРИМЕРА VI.1, при наличии корреляционных связей между главными и попутным компонентом, совершить регрессионный анализ с учетом связей между главными и попутным компонентами. Вычислить уравнение регрессии для оценки содержания попутного компонента по главным компонентам.

Ответ

1. Откройте лист 1 рабочей книги Excel, созданной при работе над ПРИМЕРОМ VI.1.

2. В пункте меню Сервис выберите строчок Анализ данных и потом укажите курсором мыши на строчок Регрессия. Надавите кнопку OK.

3. В показавшемся диалоговом окне задаем Входной промежуток Y. Для этого наведите указатель мыши на верхнюю ячейку столбца зависимых данных (E1), надавите левую кнопку мыши и, не отпуская ее, протяните указатель мыши к нижней ячейке (E51), после этого отпустите левую кнопку мыши. (Обратите внимание, что зависимые эти – это те эти, каковые предполагается вычислять).

4. Так же укажите Входной промежуток X, другими словами введите ссылку на диапазон свободных данных B1:D51. (Свободные эти – это те эти, каковые будут измеряться либо наблюдаться).

5. Установите флажок в поле Метки в первой строке. Установите флажок в поле График подбора.

6. Потом укажите выходной диапазон. Для этого поставьте тумблер в положение Выходной промежуток (наведите указатель мыши и щелкните левой кнопкой), после этого наведите указатель мыши на правое поле ввода Выходной интервали, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (G10). Щелкните левой кнопкой мыши. Надавите кнопку OK.

7. В выходном диапазоне покажутся результаты регрессионного анализа и графики предсказанных точек.

Интерпретация результатов. В таблице Дисперсионный анализ оценивается достоверность взятой модели по уровню значимости критерия Фишера (строчок Регрессия, столбец Значимость F, в примере – 0,000191, другими словами p

Потом нужно найти значения коэффициентов модели. Они определяются из таблицы в столбце Коэффициенты – в строчке Y-пересечение приводится вольный член 0,083; в строчках соответствующих переменных приводятся значения коэффициентов при этих переменных Cu = 0,016, Pb = 0,058 и Zn = 0,015. В столбце p-значение приводится достоверность отличия соответствующих коэффициентов от нуля. Все коэффициенты незначимы (0,146, 0,804, 0,093, 0,104), другими словами для всех коэффициентов p 0,05, и коэффициенты смогут принимать во внимание равными нулю.

8. Исходя из этого в модель направляться включить лишь те свободные переменные, каковые коррелируют с зависимой переменной. Выполните регрессионный анализ посредством меню Сервис/Анализ данных, установив Входной промежуток X как C1:D51, другими словами забрав в качестве свободных переменных – содержания Pb и Zn.

Интерпретация результатов. В таблице Дисперсионный анализ оценивается достоверность взятой модели по уровню значимости критерия Фишера (строчок Регрессия, столбец Значимость F, в примере – 4,75E-05, другими словами p

Значения коэффициентов модели определяются из таблицы в столбце Коэффициенты – в строчке Y-пересечение приводится вольный член 0,086; в строчках соответствующих переменных приводятся значения коэффициентов при этих переменных: Pb = 0,053 и Zn = 0,017. В столбце p-значение приводится достоверность отличия соответствующих коэффициентов от нуля. коэффициент и Свободный член при Pb незначимы, другими словами p 0,05, и коэффициенты смогут принимать во внимание равными нулю, а коэффициент при Zn значим, поскольку соответствующее p-значение – 0,0087.

9. Улучшим модель, забрав в качестве свободных переменных лишь содержание Zn. Отбросить фактор влияния Pb направляться еще и по причине того, что между Zn и Pb, существует корреляционная сообщение, о чем свидетельствует коэффициент парной корреляции равный 0,572, что кроме того немного выше коэффициента парной корреляции между Au и Zn, равного 0,545.

Выполним регрессионный анализ посредством меню Сервис/Анализ данных, установив Входной промежуток X как D1:D51.

Интерпретация результатов. В таблице Дисперсионный анализ оценивается достоверность взятой модели по уровню значимости критерия Фишера (строчок Регрессия, столбец Значимость F, в примере – 4,15E-05, другими словами p

Значения коэффициентов модели определяются из таблицы в столбце Коэффициенты – в строчке Y-пересечение приводится вольный член 0,120; в строчке переменной Zn значение коэффициента при переменной Zn = 0,023. В столбце p-значение приводится достоверность отличия соответствующих коэффициентов от нуля. Вольный член значим, другими словами p 0,05, и коэффициент при Zn значим, поскольку соответствующее p-значение – 4,15E-05.

График подбора – см. рис. VI.1. Получено уравнение регрессии Au(Zn)=0,0236*Zn+0,1204.

Потому, что точность аппроксимации недостаточна, на следующем этапе возможно постараться подобрать нелинейную модель зависимости Zn – Au, к примеру, Au(Zn)=–0,00045*Zn^2+0,03682*Zn+0,08112, для которой R-квадрат равен 0,309 (см. рис. VI.2).

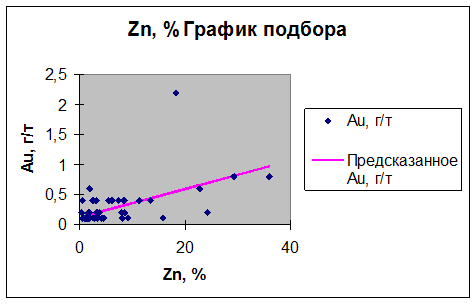
Рис. VI.1. График подбора модели посредством процедурыРегрессия

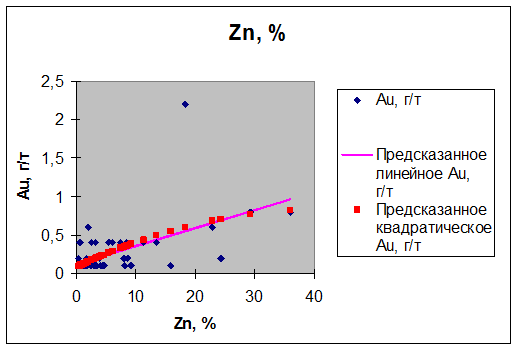
Рис. VI.2.График линейной и квадратической регрессии

10. Подобно, для всех значимых свободных переменных сделайте регрессионный анализ для данных, представленных в табл. VI.2 – VI.5.

Откройте лист 2 рабочей книги Excel, созданной при работе над ПРИМЕРОМ VI.1. Разглядите в качестве свободных переменных переменные Pb и Zn. Регрессионная модель будет смотреться как Ag(Pb,Zn)=9,300*Pb+2,670*Zn+15,426.

Откройте лист 3 рабочей книги Excel, созданной при работе над ПРИМЕРОМ VI.1. Разглядите в качестве свободной переменной переменную Zn. Регрессионная модель будет смотреться как Cd(Zn)=3,930*Zn–0,511.

Откройте лист 4 рабочей книги Excel, созданной при работе над ПРИМЕРОМ VI.1. Разглядите в качестве свободной переменной переменную Zn. Регрессионная модель будет смотреться как Sb(Zn)=92,459*Zn–161,693.

Откройте лист 5 рабочей книги Excel, созданной при работе над ПРИМЕРОМ VI.1. Разглядите в качестве свободной переменной переменную Pb. Регрессионная модель будет смотреться как Ba(Pb)=3,251*Pb+2,455.

ПРИМЕР VI.3

Требуется

По условию ПРИМЕРА VI.1:

1) проверить догадку о наличии корреляционной связи между главными и одним из попутных компонентов;

2) выяснить, с каким из главных компонентов самый тесно связан попутный компонент;

3) взять корреляционную матрицу, дать ее графическое изображение. Выделить значимые коэффициенты корреляции;

4) при наличии корреляционных связей между главными и попутным компонентом совершить регрессионный анализ с учетом связей между главными и попутным компонентами. Вычислить уравнение регрессии для оценки содержания попутного компонента по главным.

Ответ

1. Создать файл данных в программе Statistica по табл. VI.1.

2. Совершить корреляционный анализ всей выборки. Для этого в меню с главными процедурами Statistics выбрать Basic Statistics/Tables,а в показавшемся его меню – Correlation matrices.

В показавшемся диалоговом окне Product-Moment and Partial Correlations: надавить на вкладке Quickкнопку Summary: Correlation Matrix и в диалоговом окне Select one or two variable lists указать для First variable list:1–3, а для Second variable list (optional):4 (см. рис. VI.3). Потом надавить OK. Результатом будет расчет коэффициентов корреляции – рис. VI.4.

Возвратившись в диалоговое окно Product-Moment and Partial, надавить на вкладке Advanced/Plotкнопку2D scatterplot и результатом будет – расчет scatterplot (доверительный промежуток) для переменной Au зависимостей от Cu, Pb, Zn. На рис. VI.5 приведен доверительный промежуток для зависимости Au(Zn). Сравните уравнение, находящееся в верхней части графика, с уравнением, взятым в электронных таблицах Excel (см. ПРИМЕР VI.2).

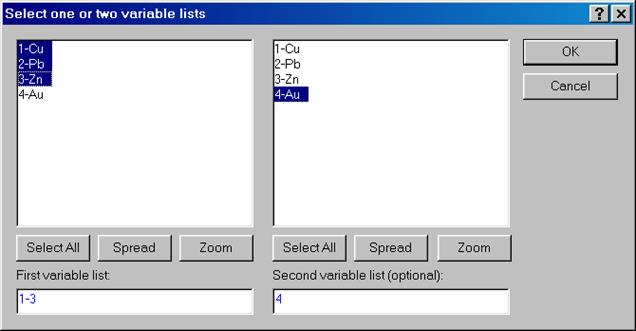
Рис. VI.3. Выбор переменных для корреляционного анализа

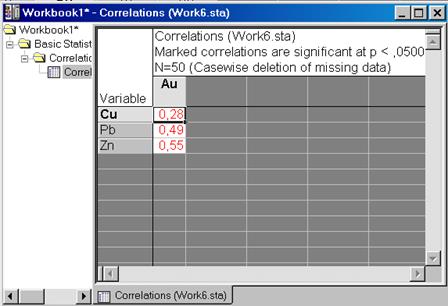
Рис. VI.4.Расчет коэффициентов корреляции

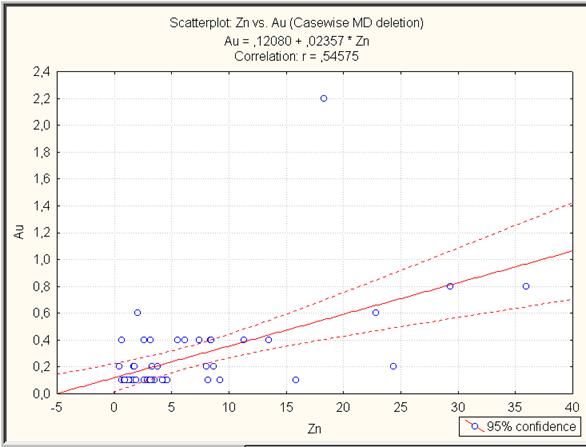
Рис. VI.5. Зависимость Au от Zn и ее доверительный промежуток

3. Так как существует корреляция между концентрациями Au и Zn, то направляться произвести регрессионный анализ. Для этого в начальном меню StatisticSвыбираем Multiple Regression.

В открывшемся диалоговом окне Multiple Linear Regression нажимаем кнопку Variables и устанавливаем, как продемонстрировано на рис. VI.6 в открывшемся диалоговом окне Select depended and independed variables lists:, зависимую и свободную переменные. Потом нажимаем OK.

Возвратившись в диалоговое окне Multiple Linear Regression, надавить OK.

Результатом будет Multiple Regression Results: – см. рис. VI.7.

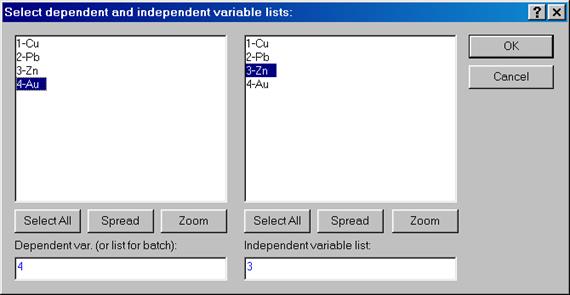
Рис. VI.6. Установка зависимой и свободной переменных для регрессионного анализа

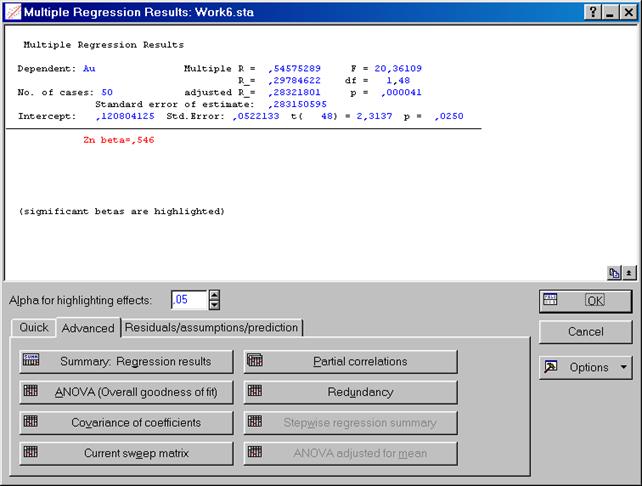
Рис. VI.7. Multiple Regression Results:

Потом, в этом диалоговом окне Multiple Regression Results:, надавить кнопку Summary: Regresion Results и возьмём таблицу статистик – см. рис. VI.8, где в столбце В указаны коэффициенты регрессии: 0,120947 – коэффициент при Zn и 0,120804 – вольный член; p-level – уровень значимости для каждого коэффициентов; beta – коэффициент корреляции. Сравните уравнение с уравнением, взятым в электронных таблицах Excel – см. ПРИМЕР VI.2.

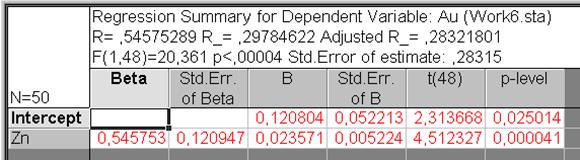
Рис. VI.8. Таблица результатов Regresion Results

4. Подобно, для всех значимых свободных переменных сделайте регрессионный анализ для данных, представленных в табл. VI.2 – VI.5.

ЛАБОРАТОРНАЯ РАБОТА № VII. МНОГОМЕРНЫЕ СТАТИСТИЧЕСКИЕ МОДЕЛИ. КЛАСТЕРНЫЙ АНАЛИЗ. ФАКТОРНЫЙ АНАЛИЗ

СТАТИСТИЧЕСКИЕ СПОСОБЫ ВЫДЕЛЕНИЯ АССОЦИАЦИЙ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ

Способы выделения парагенетических химических элементов сводятся к разделению исходных совокупностей на пара классов по степени сходства, составляющих их объектов. Наряду с этим предполагается, что степень сходства объектов, объединяемых в один класс, должна быть намного больше степени сходства между объектами из различных классов.

Базой классификации исходных совокупностей химических элементов помогают корреляционные матрицы их содержаний в изучаемых количествах (минералах, породах либо рудах), а мерой сходства – оценки парных коэффициентов их корреляции. Выделение парагенетических ассоциаций элементов сводится к обнаружению в корреляционной матрицы [R] однородных блоков (подматриц типа [Ri]), соответствующих таким совокупностям элементов, содержания которых связаны линейной хорошей зависимостью.

Строгое математическое ответ задачи классификации исходных совокупностей по корреляционным чертям фактически нереально, потому, что коэффициенты парной корреляции элементов имеют стохастическую природу, в связи с чем во многих конкретных случаях появляются возможности многовариантного группирования объектов.

РАСПОЗНАВАНИЕ ОБРАЗОВ БЕЗ ОБУЧЕНИЯ

Хорошими способами распознавания образов без обучения являются способы кластерного анализа (кластер-анализа).

Номера, приобретаемые в следствии расчета кластеров, смыслового значения не имеют. Эти номера необходимы лишь чтобы отличить один кластер от другого, исходя из этого при применении результатов кластерного анализа в других способах, к примеру в распознавании образов с обучением, порядок следования кластеров возможно любым удобным для исследователя.

Все рассмотренные потом способы смогут быть использованы как для классификации объектов, так и для классификации показателей.

МЕРЫ СХОДСТВА и МЕРЫ Различия

Виды применяемых в кластерном анализе мер сходства и различия перекликаются с философской задачей: «ищите сходство» либо «ищите различие». Меры сходства для кластерного анализа смогут быть следующих видов:

• Мера сходства типа расстояния (функции расстояния), именуемая кроме этого мерой различия. В этом случае объекты считаются тем более похожими, чем меньше расстояние между ними, исходя из этого кое-какие авторы именуют меры сходства типа расстояния мерами различия.
• Мера сходства типа корреляции, именуемая связью, есть мерой, определяющей похожесть объектов. В этом случае объекты считаются тем более похожими, чем больше связь между ними. Меры смогут быть легко приведены к прошлому типу.
• Информационная статистика.

Меры различия и информационная статистика

Применяемые наряду с этим метрики – евклидово расстояние, манхеттенское расстояние, сюпремум-норма, расстояние Махалонобиса – они отражают все многообразие подходов к решению проблемы. Первая метрика употребляется традиционно, вторая метрика есть самый известным представителем класса метрик Минковского. Расстояние Махаланобиса, по определению метрикой не являющееся, связано посредством дисперсионно-ковариационной матрицы с корреляциями переменных (параметров), и активно используется как в кластерном, так и в других способах анализа данных.

Меры сходства употребляются для способов:

• ближней связи (данный способ имеет вариант и для мер сходства);
• средней связи Кинга;
• Уорда;
• средних Мак-Куина.

Меры сходства

Связями смогут быть: коэффициент корреляции, коэффициент ассоциативности (ассоциации) и т.д. Из этих связей для количественных показателей предназначены: коэффициент корреляционного отношения Пирсона, дисперсия-ковариация. Для порядковых показателей предназначены: показатель ранговой корреляции Спирмена, коэффициент ранговой корреляции Кендалла.

Перечисленные меры сходства применяют способы:

• ближней связи (данный способ имеет вариант и для мер различия);
• корреляционных плеяд;
• большого корреляционного пути.

По умолчанию в последних двух способах в большинстве случаев классифицируются параметры (в первом классифицируются объекты), что обусловлено их классической назначением и авторской реализацией, но методом несложного транспонирования матрицы данных и перемены местами столбцов и чисел строк возможно легко поменять тип классификации на противоположный.

В комбинации с разными метриками, мерами и связями сходства других типов, перечисленные методы дают много вариантов ответа задачи классификации без обучения. Результаты классификации различными способами, в большинстве случаев, принципиально не различаются, и выбор того либо иного способа есть делом традиции школы и вкуса исследователя.

КЛАСТЕРНЫЙ АНАЛИЗ

Способами кластерного анализа решается задача разбиения (классификации, кластеризации) множества объектов так, дабы все объекты, находящиеся в собствености одному кластеру (классу, группе) были более похожи, чем на объекты вторых кластеров. В отечественной литературе синонимом термина «кластерный анализ» есть термин «таксономия». В зарубежной литературе под таксономией традиционно понимается классификация растений и видов животных.

Рассматриваются следующие способы кластерного анализа:

• Иерархические способы:

o способ ближней связи,

o способ средней связи Кинга,

o способ Уорда.

• Итеративные способы группировки:

o способ k-средних Мак-Куина.

• Методы типа разрезания графа:

o способ корреляционных плеяд Терентьева,

o вроцлавская таксономия.

Классифицируемы смогут быть как параметры, так и объекты.

1) СПОСОБ БЛИЖНЕЙ СВЯЗИ

Данный способ есть самым несложным для понимания из иерархических агломеративных способов кластерного анализа. Способ и начинает процесс классификации с объединения и поиска двух самые похожих объектов в матрице сходства. На следующем этапе находятся два очередных самые похожих объекта, и процесс повторяется до полного исчерпания матрицы сходства.

В ходе кластеризации способом ближней связи очевидно прослеживается образование цепочек объектов. Так, для выделения кластеров по окончании окончания процесса кластеризации требуется задаться некоторым пороговым уровнем сходства, на котором выделяется число кластеров, большее единицы. Процедура не всегда обнаруживает такое свойство, как образование одного громадного кластера на последней стадии кластеризации, и довольно часто заканчивается явным разделением всех предъявленных объектов на кластеры.

2) СПОСОБ СРЕДНЕЙ СВЯЗИ КИНГА

Способ средней связи подобен способу ближней связи. Отличие в том, что на каком-либо этапе ранее объединенные в один кластер объекты считаются одним объектом с усредненными по кластеру параметрами.

3) СПОСОБ УОРДА

Этот способ напоминает способ средней связи Кинга. Изюминок пребывает в том, что основанием для помещения объекта в кластер есть не близость двух объектов в каком-либо смысле, в зависимости от меры сходства, а минимум дисперсии в кластера при помещении в него текущего классифицируемого объекта.

4) СПОСОБ K-СРЕДНИХ МАК-КУИНА

Теоретическое обоснование способа k-средних (k внутригрупповых средних) относительно легко, логично и возможно отыскано во многих источниках. Принцип классификации сводится к некоему, быть может, случайному, исходному разбиению множества объектов на заданное число кластеров (классов, групп, популяций), последующему отнесению остальных объектов к ближайшим кластерам, пересчету новых «центров тяжести» кластеров и продолжению обрисованной процедуры, пока не будет получено некое оптимальное разбиение. Кластеризация в большинстве случаев длится, пока новые «центры тяжести» кластеров не прекратят различаться от ветхих «центров тяжести». Изюминкой способа есть то, что выделенные в следствии расчетов кластеры не будут пересекаться – гарантируется, что любой классифицированный объект будет отнесен лишь к одному кластеру.

В визуализации результатов кластеризации способом k-средних нет необходимости, не смотря на то, что может оказаться наглядным и прекрасным изображение пространственных эллипсоидов (лишь для размерности не более 3, для большей размерности употребляются двумерные срезы пространства), coдержащих классифицированные объекты.

09. Закон нормального распределения

Интересные записи:

• Приложение i. значения функции нормального распределения с параметрами 0 и 1 (для отрицательных значений z) 3 глава
• Приложения (предполагаемые, т.к. студент может на свое усмотрение добавить что-то)
• Приложение i. значения функции нормального распределения с параметрами 0 и 1 (для отрицательных значений z) 7 глава
• Применение гаси при тушении пожаров