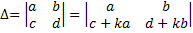Определители, их основные свойства и вычисление.

Определители, их вычисление и основные свойства.

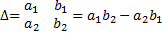
Минором элемента именуется определитель (n-1) порядка, полученный из исходного определителя удалением i-строки и j-столбца

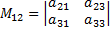
Алгебраическим дополнением элемента именуется минор

Следствие из теоремы Лапласа — определитель равен сумме произведений элементов какой-либо строки(столбца), умноженных на их алгебраическое дополнение.

Свойства определителя:

1. В случае, если строки либо столбцы поменять местами, то его величина не изменится

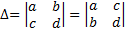Это свойство определяет, что строки и столбцы определителя равноправны

(Операция замены строчков столбцами с сохранением нумерации именуется транспонированием)

2. В случае, если все элементы строчка(столбца) определителя равны нулю, то и сам определитель равен нулю.

3. В случае, если в определителе элементы строчка(столбца) имеют неспециализированный множитель, то его возможно вынести за символ определителя

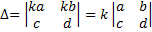
4. В случае, если определитель имеет две однообразные строчки(столбца), то он равен нулю.

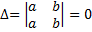
5. В случае, если в определителе переставить местами две строки(столбца), то определитель поменяет символ на противоположный

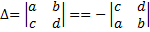
6. В случае, если в определителе строчка(столбцы) пропорциональны элементам второй строки(столбца), то определитель равен нулю

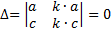
7. В случае, если все элементы строчка либо столбца представлены в виде суммы двух слагаемых, то таковой определитель возможно представить в виде суммы двух определителей

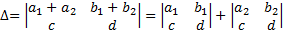
8. В случае, если к элементам некоей строки либо столбца прибавить соответствующие элементы второй строки либо столбца, умноженных на любой множитель k, то величина определителя не изменится

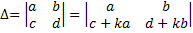
Совокупности линейных алгебраических уравнений, формулы Крамера.

Разглядим совокупность линейных уравнений третьего порядка:

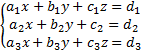
Запишем определитель совокупности, другими словами определитель, складывающийся из коэффициентов при переменных:

Пускай

Составим определители, заменяя в определителе совокупности столбец коэффициентов при выбранной переменной столбцом, складывающимся из свободных участников:

,

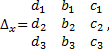
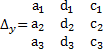В случае, если определитель совокупности отличен от нуля, то совокупности линейных уравнений имеют единственное ответ, которое определяется формулами

,

Так,

•в случае, если определитель совокупности отличен от нуля, то совокупность совместная определенная (имеет 1 ответ)

•в случае, если определитель равен нулю, то вероятны два случая:

а) в случае, если хотя бы один определитель 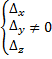, то совокупность несовместна (ответов нет)

б) в случае, если все определители 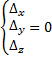, совокупность совместная неизвестная (нескончаемое множество ответов)

3. Определение вектора, модуль вектора, коллинеарные и компланарные векторы, равенство векторов.

Вектором именуется направленный отрезок, другими словами отрезок, с указанными начальной и конечной точками

В

А

Модулем (длиной) вектора именуется протяженность отрезка АВ —

Векторы, лежащие на одной прямой либо на параллельных прямых, именуются коллинеарными

Коллинеарные векторы смогут быть сонаправлены либо

противоположнонаправлены

Векторы, лежащие в одной плоскости либо в параллельных плоскостях, именуются компланарными

Два вектора именуются равными, если они компланарны, коллинеарны и их длины равны

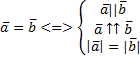
Линейные операции над векторами: вычитание и сложение векторов, умножение вектора на число, свойства этих операций.

I) Сложение векторов

а) правило треугольника

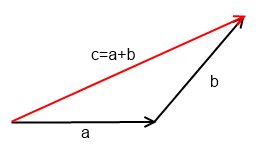
б) правило параллелограмма

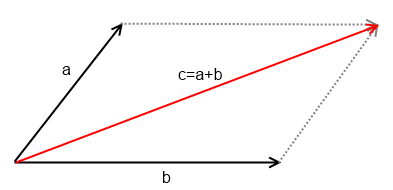
в) правило ломаной

Пускай даны пара векторов. Тогда, дабы выстроить сумму этих векторов, необходимо расположить эти векторы так, дабы начало последующего совпадало с финишем прошлого, взяв так ломаную. Тогда вектор, замыкающий эту ломаную, начало которого сходится с началом первого вектора, а финиш с финишем последнего, будет суммой векторов.

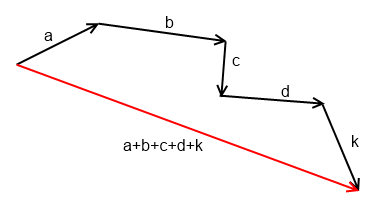
Свойства операции сложения:

1) коммуникативность a+b=b+a

2) ассоциативность a+(b+c)=(a+b)+с

3) a+0=a

II) Разностью векторов именуется вектор таковой, что

III) Умножение вектора на число

Произведением вектора на число , именуется вектор , коллинеарный вектору , протяженность которого равна , причем

и

Умножение вектора на n — это растяжение этого вектора в n раз

Свойства умножения:

1) коммуникативность

2) ассоциативность

3) дистрибутивность

Кое-какие частные виды уравнения прямой: уравнение прямой с угловым коэффициентом, уравнение прямой в отрезках, уравнение прямой, проходящей через данную точку в данном направлении, уравнение прямой, проходящей через две эти точки.

С заданным угловым коэффициентом:

Уравнение прямой в отрезках: 1) С=0, (прямая проходит через т.(0;0)

2) B=0, (прямая ? ox)

3)B=0, C=0, x=0 (ось ординат либо || ей прямая)

4) A=0, (прямая? oy)

5) A=0, C=0, y=0 (ось абсцисс либо || ей прямая)

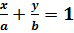, где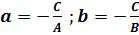

Уравнение прямой, проходящей через две эти точки:

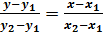
Уравнение прямой, проходящей через данную точку в данном направлении:

?

IV) Парабола

Каноническое уравнение параболы

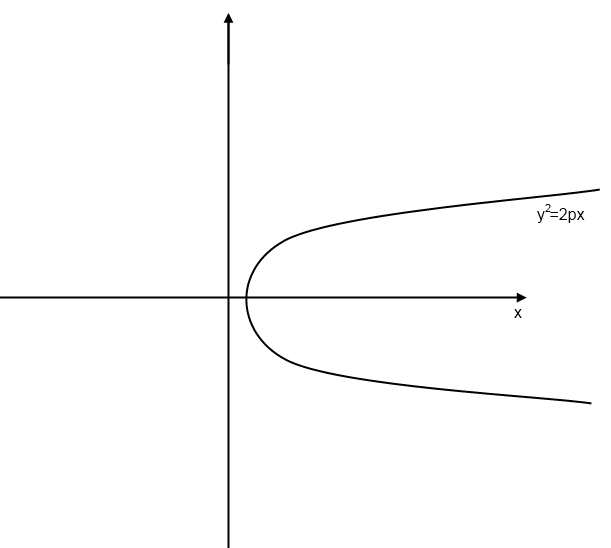
Парабола не имеет асимптот. Осью симметрии есть ох.

Вершина в т.О.

Циллиндрическая поверхность

Пускай на хоу заданв прямая . Через каждую точку совершим прямые, параллельные оz. Эти прямые образуют поверхность, которую именуют циллиндрической поверхностью.

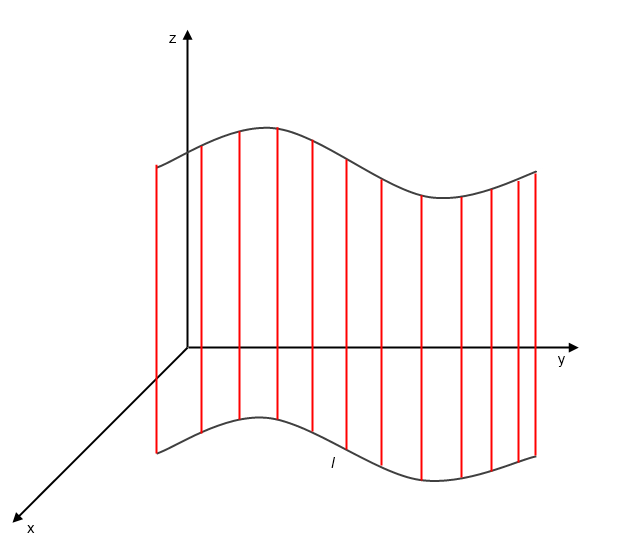
Кривая — направляющая

В зависимости от направляющей, выделяют три вида циллиндрических поверхностей:

I) 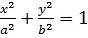-эллиптический циллиндр

II) 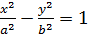— гиперболический циллиндр

III) — пара(барА-барА-парА-берЕ-берЕ)болический циллиндр

Эллипсоид

Эллипсоидом именуется поверхность, которая в прямоугольной совокупности координат определяется уравнением:

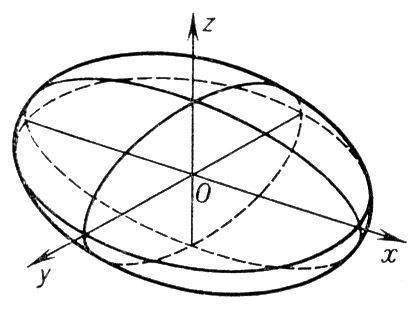
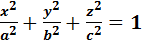
Конус -поверхность, заданная уравнением: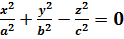

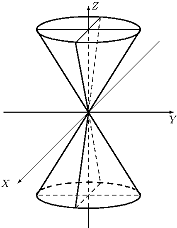
Гиперболоид

Однополостный гиперболоид определяется уравнением: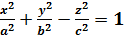

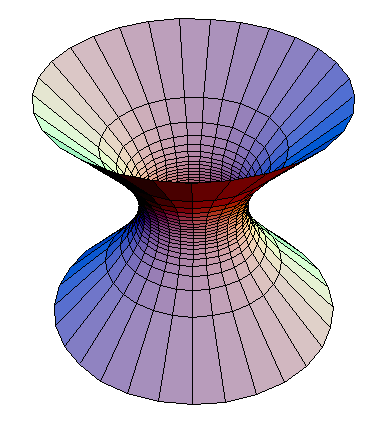
Двуполостный гиперболоид определяется уравнением: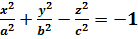

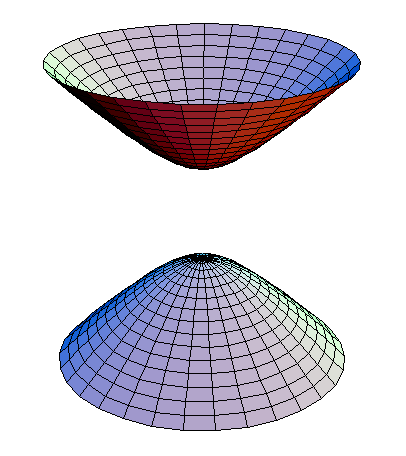
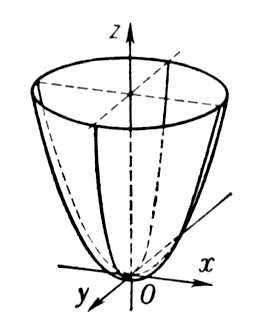
Параболоид

Эллиптический параболоид — поверхность, определяемая уравнением: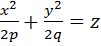

29. Матрицы, определения и основные понятия, сложение матриц, умножение матриц на число, умножение матриц, свойства этих операций; правила и обратная матрица её вычисления, ранг матрицы.

Матрицей размера m x n именуется прямоугольная таблица, содержащая чисел, складывающаяся из m строчков и n столбцов.

Элементы матрицы обозначаются , где — номер строчка, в которой находится элемент, а — номер столбца.

Основной диагональю матрицы именуется диагональ, совершённая из левого верхнего угла матрицы в правый нижний.

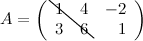
Побочной диагональю матрицы именуется диагональ, совершённая из левого нижнего угла матрицы в правый верхний.

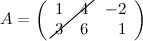
Матрица именуется верхней треугольной матрицей, в случае, если все элементы ниже основной диагонали равны нулю.

Матрица именуется нижней треугольной матрицей, в случае, если все элементы выше основной диагонали равны нулю.

Ступенчатой именуется матрица, которая содержит строчков и у которой первые диагональных элементов ненулевые, а элементы, лежащие ниже основной диагонали и элементы последних строчков равны нулю, другими словами это матрица вида:

Две матрицы именуются равными, если они имеют однообразные размеры и их соответствующие элементы равны:

Операции над матрицами:

Произведением матрицы на числоназывается матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Суммой матриц и одного размера именуется матрица для того чтобы же размера, приобретаемая из исходных методом сложения соответствующих элементов.

Свойства линейных операций:

Везде потом матрицы , и — матрицы одного размера.

1. Ассоциативность
2. , где — нулевая матрица соответствующего размера.
4. Коммутативность
5. Дистрибутивность

Произведением матрицы на матрицу именуется матрица такая, что элемент матрицы , стоящий в -ой строке и -ом столбце, т.е. элемент , равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -ого столбца матрицы .

Пример:

Задание. Отыскать , в случае, если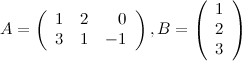

Ответ. Так как , а , то в следствии возьмём матрицу размера , т.е. матрицу вида 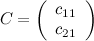. Отыщем элементы данной матрицы:

Так, приобретаем, что:

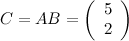
Все вычисления возможно было сделать в более компактном виде:

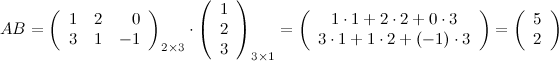
Ответ.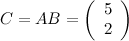

Свойства произведения матриц:

1. Ассоциативность
2. Ассоциативность по умножению
3. Дистрибутивность ,
4. Умножение на единичную матрицу
5. В общем случае умножение матриц не коммутативно, т.е.

Невырожденной именуется квадратная матрица, определитель которой не равен нулю. Квадратная матрица именуется вырожденной, в случае, если ее определитель равен нулю.

Квадратная матрица именуется обратной к невырожденной матрице , в случае, если , где — это единичная матрица соответствующего порядка.

Свойства обратной матрицы:

1.

2.

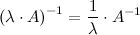
3.

4.

Теорема. В случае, если к квадратной матрице дописать справа единичную матрицу того же порядка и посредством элементарных преобразований над строчками добиться того, дабы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

Пример:

Задание. Для матрицы 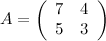отыскать обратную способом присоединенной матрицы.

Ответ. Приписываем к заданной матрице справа единичную матрицу второго порядка:

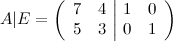
От первой строчки отнимаем вторую (для этого от элемента первой строчки отнимаем соответствующий элемент второй строки):

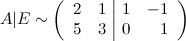
От второй строчки отнимаем две первых:

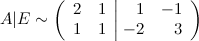
Первую и вторую строчки меняем местами:

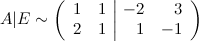
От второй строчки отнимаем две первых:

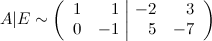
Вторую строчок умножаем на (-1), а к первой строке прибавляем вторую:

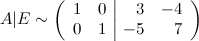
Итак, слева взяли единичную матрицу, соответственно матрица, стоящая в правой части (справа от вертикальной черты), есть обратной к исходной.

Так, приобретаем, что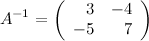

Ответ.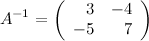

Облегченный вариант:

Для матрицы второго порядка возможно мало уменьшить нахождение обратной, применяя следующий метод:

Ход 1. Находим определитель заданной матрицы, если он равен нулю, то делаем вывод, что обратной матрицы не существует, в противном случае переходим к следующему шагу.

Ход 2. Элементы, стоящие на основной диагонали меняем местами, а у элементов побочной диагонали меняем символ на противоположный.

Ход 3. Делим все элементы на и приобретаем обратную матрицу.

Рангом матрицы именуется ранг её совокупности строчков либо столбцов. Обозначается

На практике для нахождения ранга матрицы применяют следующее утверждение: ранг матрицы равен количеству ненулевых строчков по окончании приведения матрицы к ступенчатому виду.

Корень n-степени

Уравнение вида имеет ровно корней , каковые возможно отыскать по формуле:
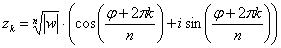, где – это модуль комплексного числа , – его довод, а параметр принимает значения:

Касательная

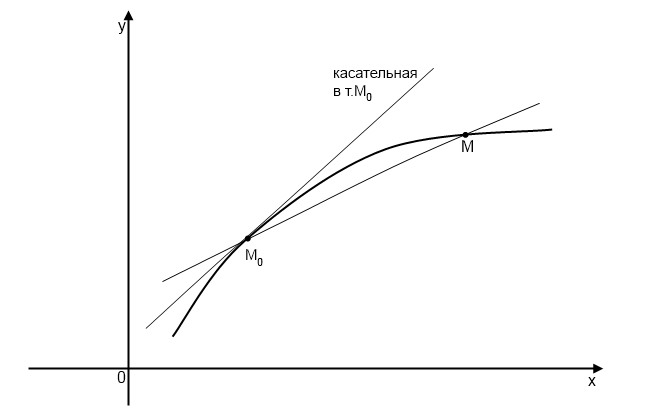Касательной к точке именуется предельное положение секущей при рвении точки M к точке по кривой.

Уравнение касательной:

Нормалью к графику функции в точке прямая, проходящая через эту точку перпендикулярно касательной.

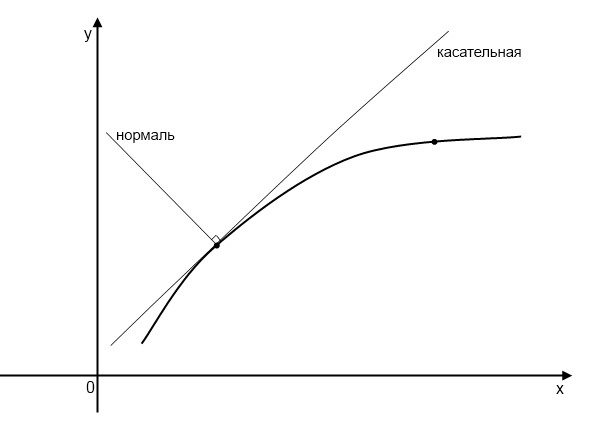
Нормаль ? касательной = , где k-коэффициент касательной.

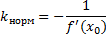
Уравнение нормали в точке :

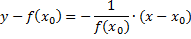
Правило Лопиталя.

Производная оказывает помощь раскрыть пределы и раскрывать неопределенности вида:

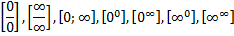
Т.1:

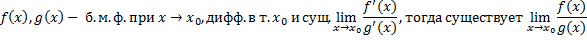
Т.2:

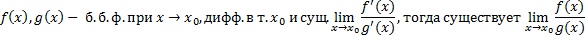
Асимптоты кривой.

Асимптота кривой с нескончаемой ветвью — прямая, владеющая тем свойством, что расстояние от точки кривой до данной прямой пытается к нулю при удалении точки на протяжении ветви в бесконечность.

Для преувеличения асимптотами являются ординат и оси абсцисс. Кривая может приближаться к собственной асимптоте, оставаясь с одной стороны от нее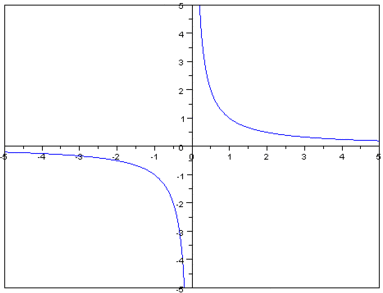

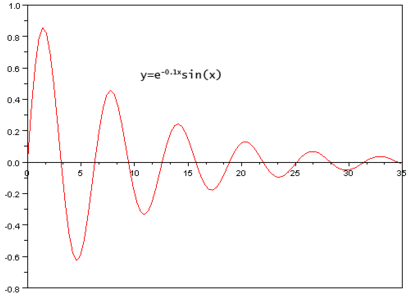
Затухающие колебания

Кривая может нескончаемое множество раз пересекать асимптоту

Определители, их вычисление и основные свойства.

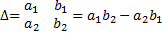
Минором элемента именуется определитель (n-1) порядка, полученный из исходного определителя удалением i-строки и j-столбца

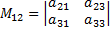
Алгебраическим дополнением элемента именуется минор

Следствие из теоремы Лапласа — определитель равен сумме произведений элементов какой-либо строки(столбца), умноженных на их алгебраическое дополнение.

Свойства определителя:

1. В случае, если строки либо столбцы поменять местами, то его величина не изменится

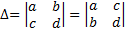Это свойство определяет, что строки и столбцы определителя равноправны

(Операция замены строчков столбцами с сохранением нумерации именуется транспонированием)

2. В случае, если все элементы строчка(столбца) определителя равны нулю, то и сам определитель равен нулю.

3. В случае, если в определителе элементы строчка(столбца) имеют неспециализированный множитель, то его возможно вынести за символ определителя

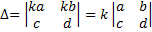
4. В случае, если определитель имеет две однообразные строчки(столбца), то он равен нулю.

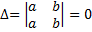
5. В случае, если в определителе переставить местами две строки(столбца), то определитель поменяет символ на противоположный

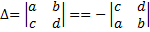
6. В случае, если в определителе строчка(столбцы) пропорциональны элементам второй строки(столбца), то определитель равен нулю

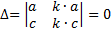
7. В случае, если все элементы строчка либо столбца представлены в виде суммы двух слагаемых, то таковой определитель возможно представить в виде суммы двух определителей

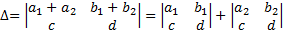
8. В случае, если к элементам некоей строки либо столбца прибавить соответствующие элементы второй строки либо столбца, умноженных на любой множитель k, то величина определителя не изменится

4. Что такое определитель матрицы? — bezbotvy

Интересные записи:

• Организационно-технологическая часть
• Организация грузовых перевозок на автомобильном транспорте
• Организация мыслительных процессов
• Организация геодезических работ на строительной площадке.