Кривые второго порядка: эллипс, парабола, гипербола

1. Эллипсом именуется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

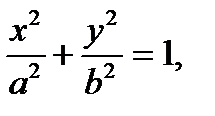(21)

где 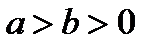. (22)

Уравнение (21) именуется каноническим уравнением эллипса.

Параметры эллипса:

Точки F1(–c, 0) и F2(c, 0), где 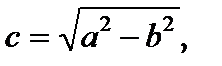именуются фокусами эллипса, наряду с этим величина 2c определяет междуфокусное расстояние.

Точки А1(–а, 0), А2(а, 0), В1(0, –b), B2(0, b) именуются вершинами эллипса, наряду с этим А1А2 = 2а образует громадную ось эллипса, а В1В2 – малую, 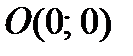– центр эллипса.

-a2

-b2

M

B1

B2

A1

A2

b

а

а

у

х

F2

F1

D2

D1

-c2

с

s2

s1

Рис. 12

Главные параметры эллипса, характеризующие его форму:

? = с/a – эксцентриситет эллипса;

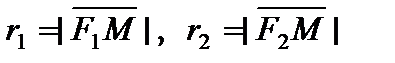– фокальные радиусы эллипса (точка М в собственности эллипсу), причем r1 = a + ?x, r2 = a – ?x;

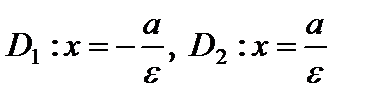– директрисы эллипса.

Для эллипса справедливо: 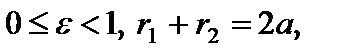директрисы не пересекают внутреннюю область и границу эллипса, и владеют свойством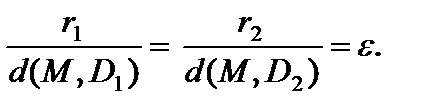

Эксцентриситет эллипса высказывает его меру «сжатости».

2. В случае, если b a 0, то эллипс кроме этого задается уравнением (21), для которого вместо условия (22) выполняется условие

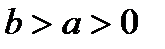. (23)

Тогда 2а – малая ось, 2b – громадная ось, 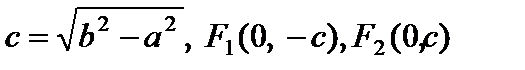– фокусы (рис. 13). Наряду с этим r1 + r2 = 2b, ? = c/b, директрисы определяются уравнениями

х

-a2

-b2

B1

B2

A1

A2

b

а

b

у

F2

F1

D2

D1

-c2

с

Рис. 13

При условии 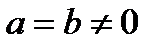имеем (в виде частного случая эллипса) – окружность радиуса R = a. Наряду с этим с = 0, соответственно, ? = 0.

Точки эллипса владеют характеристическим свойством: сумма расстояний от каждой из них до фокусов имеется величина постоянная, равная 2а (рис. 12).

3. Для параметрического задания эллипса (21) в случаях (22) и (23) в качестве параметра t возможно забрана величина угла между радиус-вектором точки, лежащей на эллипсе, и хорошим направлением оси Ox:

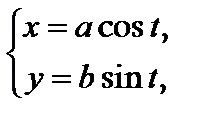где

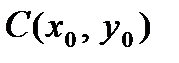4. В случае, если центр эллипса с полуосями находится в точке , то его уравнение имеет форму

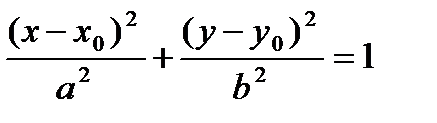. (24)

Преувеличением именуется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению

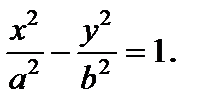(25)

где .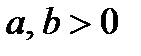

Параметры преувеличения:

Точки F1(–c, 0), F2(c, 0), где 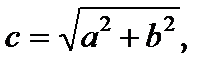именуются фокусами преувеличения, наряду с этим величина 2с (с a 0) определяет междуфокусное расстояние. Точки А1(–а, 0), А2(а, 0) именуются вершинами преувеличения, наряду с этим А1А2 = 2а образует настоящую ось преувеличения, а В1В2 = 2b – мнимую ось (В1(0, –b), B2(0, b)), О – центр преувеличения.

а

-а

b

-b

l1

l2

D1

D2

B1

B2

F1

F2

A1

A2

Рис. 19

Величина 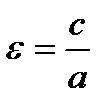именуется эксцентриситетом преувеличения, она характеризует меру «сжатости» преувеличения;

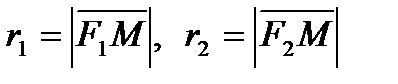– фокальные радиусы преувеличения (точка М в собственности преувеличении), причем r1 = a + ?x, r2 = –a + ?x для точек правой ветви преувеличения, r1 = – (a + ?x), r2 = – (–a + ?x) – для точек левой ветви;

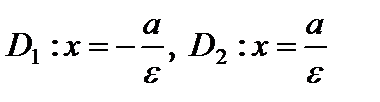– директрисы преувеличения;

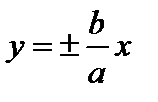– уравнения асимптот.

Для преувеличения справедливо: ? 1, директрисы не пересекают внутреннюю область и границу преувеличения, и владеют свойством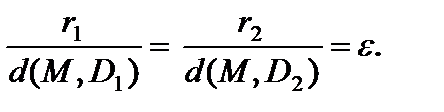

Говорят, что уравнение

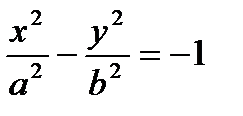(26)

задает уравнение преувеличения, сопряженной данной (рис. 20). Его возможно записать кроме этого в виде

.

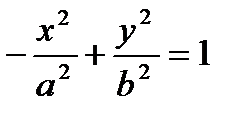При таких условиях ось 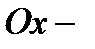мнимая, фокусы лежат на оси 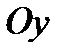. Все остальные параметры определяются подобно как для преувеличения (25).

а

-а

b

-b

D1

D2

B1

B2

F1

F2

A1

A2

-с

с

Рис. 20

Точки преувеличения владеют серьёзным характеристическим свойством: безотносительное значение разности расстояний от каждой из них до фокусов имеется величина постоянная, равная 2a (рис. 19).

Для параметрического задания преувеличения в качестве параметра t возможно забрана величина угла между радиус-вектором точки, лежащей на преувеличении, и хорошим направлением оси Ox:

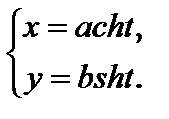
Параболой именуется геометрическое место точек плоскости, координаты которых удовлетворяют уравнению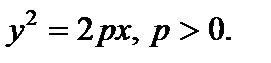

Параметры параболы:

Точка F(p/2, 0) именуется фокусом параболы, величина p – параметром, точка О(0, 0) – вершиной. Наряду с этим прямая OF, довольно которой парабола симметрична, задает ось данной кривой.

y

p

–1

х

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA38C+1MMA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE74LfITzBy7Km9SBL17QsguB6UPx7fjRv 22LzUpusVj+9EQSPw8z8hplmnanFhVpXWVYQjyIQxLnVFRcK9rv55xcI55E11pZJwY0cZGm/N8VE 2ytv6LL1hQgQdgkqKL1vEildXpJBN7INcfD+bGvQB9kWUrd4DXBTy3EUTaTBisNCiQ3NSspP23+j wB/iVd7d7Rnnv8doEX8sN+vTUqnhoPv5BuGp8+/wq73QCgIRnmfCEZDpAwAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEA38C+1MMAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== /

–p/2

Р/2

Р

D

r

F

Рис. 24

Величина 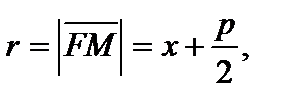где M(x, y) – произвольная точка параболы, именуется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина 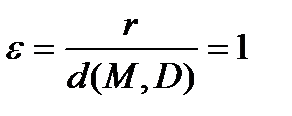именуется эксцентриситетом параболы.

Главное характеристическое свойство параболы: все точки параболы равноудалены от фокуса и директрисы (рис. 24).

Существуют иные формы канонического уравнения параболы, каковые определяют другие направления ее ветвей в совокупности координат (рис. 25).:

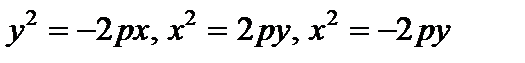
y

х

–p/2

Р/2

D

F

y

х

–p/2

Р/2

D

F

P

p

y

х

–p/2

Р/2

D

–F

P

p

Рис. 25

Для параметрического задания параболы в качестве параметра t возможно забрана величина ординаты точки параболы:

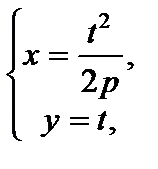
где t – произвольное настоящее число.

Поверхности второго порядка

Поверхностью второго порядка именуется поверхность S, неспециализированное уравнение которой в декартовой прямоугольной совокупности координат имеет форму

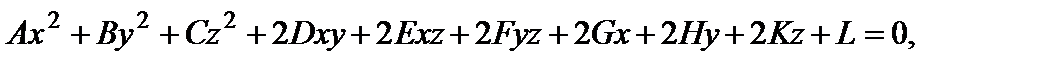(22)

где коэффициенты при одночленах второй степени в один момент не равны нулю.

Существует девять типов невырожденных поверхностей, уравнения которых посредством преобразования координат смогут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и именуются каноническими уравнениями:

1. Эллипсоид: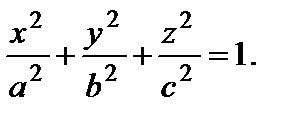

2. Гиперболоид

1) однополостный: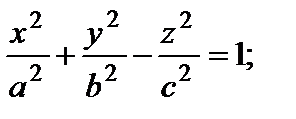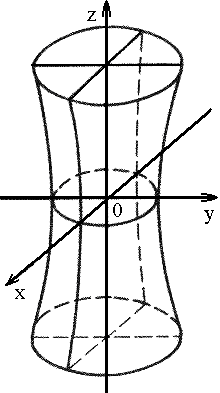

2) двуполостный: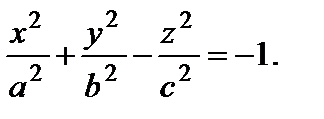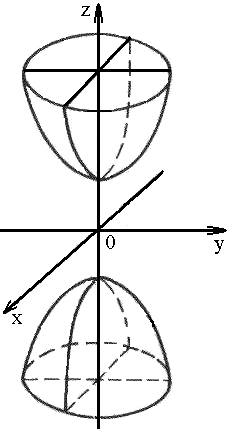

3. Конус второго порядка: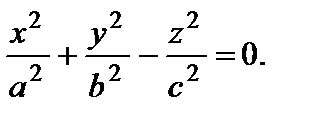

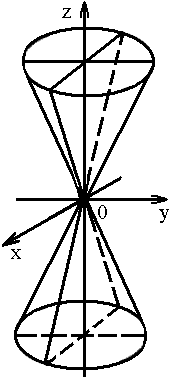
4. Параболоид

1) эллиптический: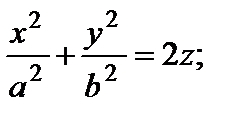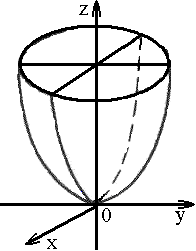

2) гиперболический: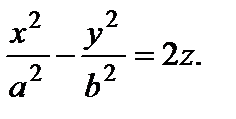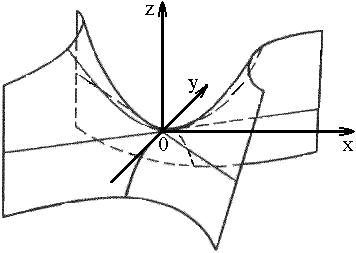

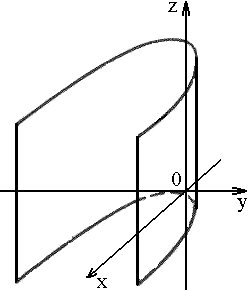
5. Цилиндр

1) эллиптический: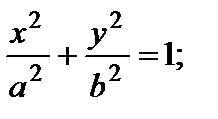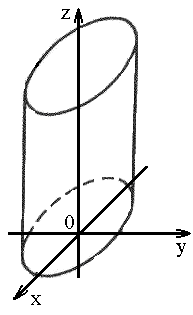

2) гиперболический: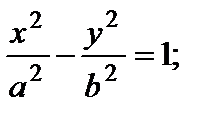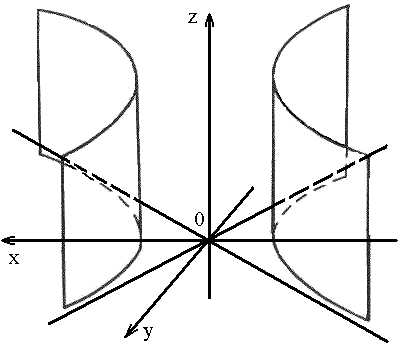

3) параболический: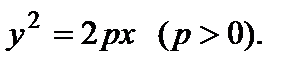

Главным способом изучения формы поверхности есть способ сечений, что пребывает в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а после этого на основании вида взятых в сечениях линий делается вывод о виде поверхности. Так изучаются фундаментальные геометрические особенности невырожденных поверхностей второго порядка на базе их канонических уравнений.

Наряду с этим, в то время, когда в общем уравнении поверхности коэффициенты 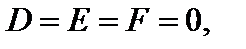приведение к каноническому виду осуществляется посредством способа выделения полных квадратов.

В определенных случаях уравнение (22) поверхности возможно приведено к уравнениям, задающим так именуемые вырожденные поверхности. Приведем примеры таких случаев.

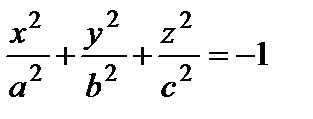– безлюдное множество точек (мнимый эллипсоид);

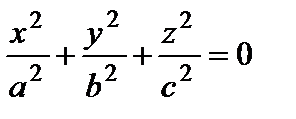– точка (0, 0, 0);

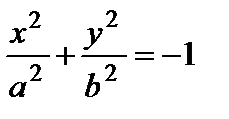– безлюдное множество точек (мнимый эллиптический цилиндр);

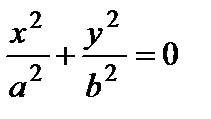–прямая (ось Oz);

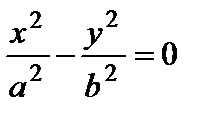– пара пересекающихся плоскостей;

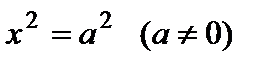– пара параллельных плоскостей;

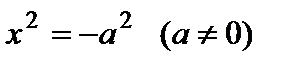– безлюдное множество точек;

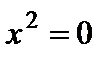– плоскость (пара совпадающих плоскостей).

действия и Матрицы над ними

Матрицейназывается прямоугольная таблица, составленная из элементов некоего множества. Горизонтальные последовательности таковой таблицы именуются строчками матрицы, а вертикальные – ее столбцами. Матрицы обозначают A, B, C, X … . Запись aij употребляется для указания расположения элемента матрицы (i – номер строчка, j – номер столбца ). Числовую матрицу размера 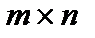(другими словами складывающуюся из m строчков и n столбцов чисел) в общем случае записывают в виде

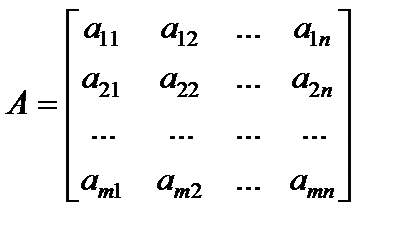либо в более компактной форме ,

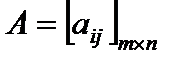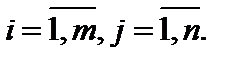
Ee обозначают кроме этого .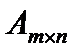

При 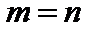матрицу именуют квадратной и в большинстве случаев обозначают An. Элементы aii, 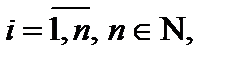таковой матрицы образуют ее основную диагональ.

Квадратная матрица вида

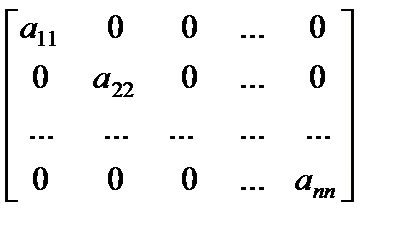, (1)

где 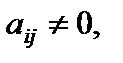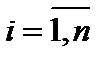, именуется диагональной. В случае, если 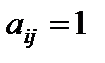для любого 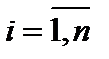, то матрица (1) именуется единичной и обозначается En.

Верхней и нижней треугольной матрицами именуются квадратные матрицы вида

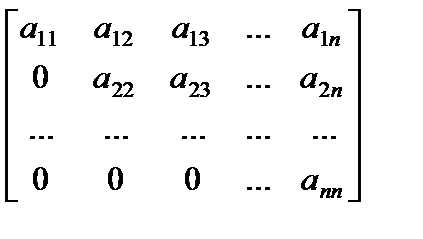либо 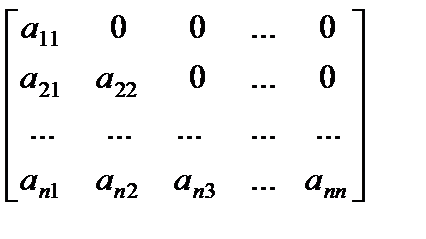соответственно.

Трапециевидной матрицей именуется матрица вида

, где числа a11, a12, …, akk хороши от нуля.

Нулевой матрицей именуется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.

Две матрицы однообразного размера

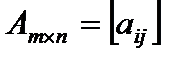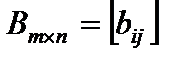и (2)

именуются равными, в случае, если 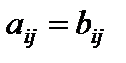для всех .

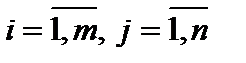Суммой матриц (2) именуется матрица A+B размера m?n, складывающаяся из элементов 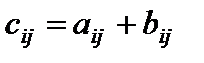, где .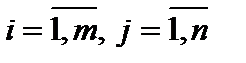

Произведением матрицы Am?n на число ? именуется матрица .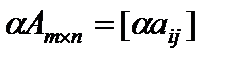

Разностью матриц (2) именуется матрица A–B = A+ (–1)B.

Свойства опреаций умножения и сложения матриц на число:

1)

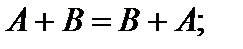
2)

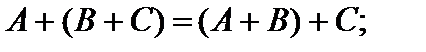
3) 0·A=О;

4)

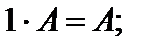
5)

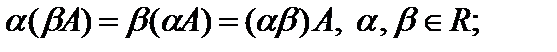
6)

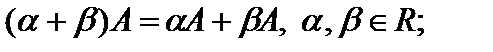
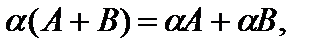
7) 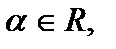A и B – матрицы однообразного размера.

Для матриц A и B возможно введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равняется количеству строчков матрицы B.

Произведением матрицы Al?m на матрицу Bm?n именуется матрица 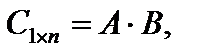элементы которой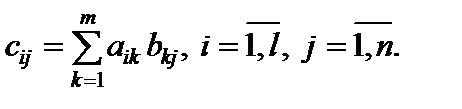

Свойства операции умножения матриц:

1)

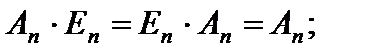
2)

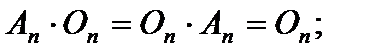
3)

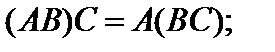
4)

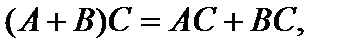
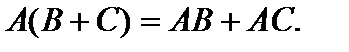
В общем случае из существования AB не нужно существование BA. Кроме того в случае, если оба эти произведения выяснены, они не всегда равны. Матрицы, для которых 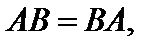именуются коммутативными.

Пускай A – квадратная матрица. Тогда k-я степень ( 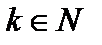) матрицы A определяется равенством 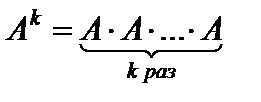. По определению принимают 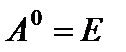при условии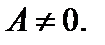

Матрица AT , полученная из матрицы A заменой столбцов строчками с теми же номерами, именуется транспонированной к матрице A, другими словами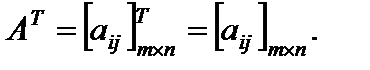

Свойства операции транспонирования матриц:

1)

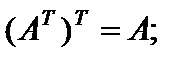
2)

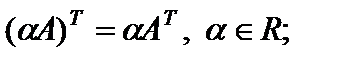
3)

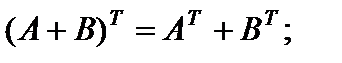
4)

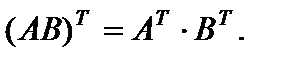
В случае, если для квадратной матрицы A выполняется соотношение 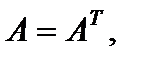то матрица A именуется симметрической матрицей, а вдруг 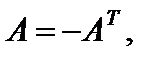– то кососимметрической.

Элементарными преобразованиями над строчками матрицы A именуют следующие операции:

1) перестановку строчков;

2) умножение строчка на ненулевое число;

3) прибавление к элементам строчка соответствующих элементов второй строки, умноженных на ненулевое число.

Говорят, что матрица A эквивалентна матрице B (пишут: A~B), в случае, если матрица B взята из A при помощи элементарных преобразований строчков.

61. Совокупности линейных уравнений. Правило Крамера

Совокупность линейных алгебраических уравнений (либо линейная совокупность) имеет форму:

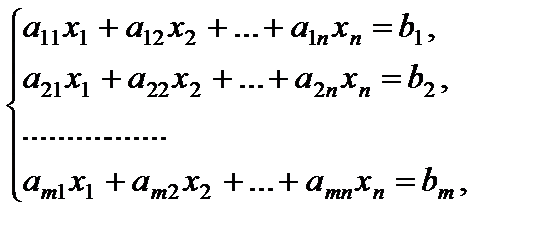(1)

где aij и bj –заданные числа.

Эту совокупность возможно записать в матричной форме

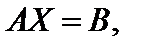(2)

где 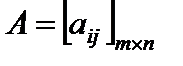– матрица совокупности складывающаяся из коэффициентов aij,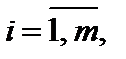

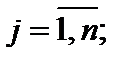
B – матрица-столбец свободных элементов bj,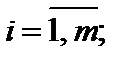

X – матрица-столбец малоизвестных, т. е. такая, которая обращает матричное уравнение (2) в равенство (есть ответом этого уравнения).

Совокупность (1) именуется совместной, в случае, если у нее существует хотя бы одно ответ, в другом случае она именуется несовместной. Две совокупности именуются эквивалентными (равносильными), в случае, если множества их ответов совпадают.

Ответ на вопрос о совместимости совокупности дает теорема Кронера-Копелли: чтобы совокупность (1) была совместной, нужно и достаточно, дабы

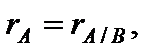
где 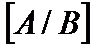– расширенная матрица совокупности (1), т.е. матрица свободных участников.

Разглядим совокупность 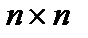, имеющую вид:

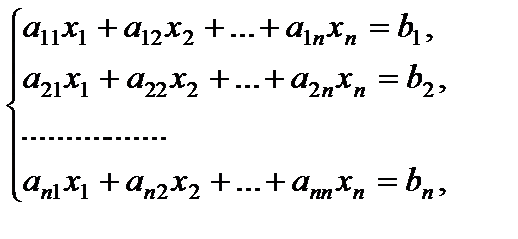(3)

либо в матричном виде

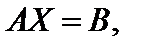
где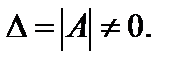

Способы ответа

Способ обратной матрицы пребывает в ответе матричного уравнения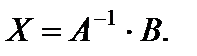

Способ Крамера: для нахождения малоизвестных нужно применять формулы

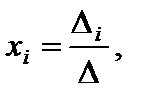(4)

где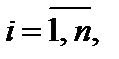

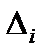– определитель, приобретаемый из определителя совокупности (3) заменой i-го столбца столбцом свободных участников.

Формулы (4) именуются формулами Крамера.

Ответ произвольной линейной совокупности (1) из m уравнений и n малоизвестных начинается с нахождения ранга. Пускай и совокупность (1) сведена к эквивалентной совокупности

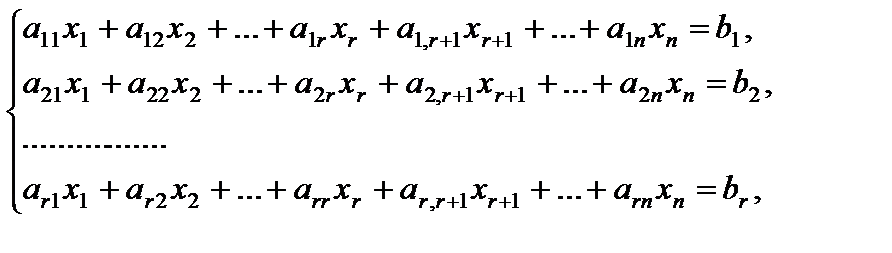(5)

В случае, если 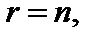то совокупность (5) имеет единственное ответ, которое возможно взять вышеуказанными способами, в случае, если 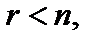то существует нескончаемое множество ответов. Для его получения малоизвестные x1, x2, …, xr именуют базовыми, xr+1, xr+2, …, xn – свободными, совокупность (5) записывается в виде:

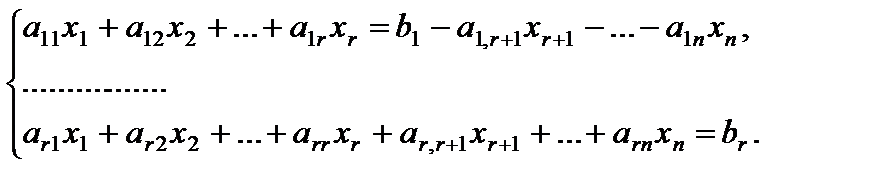
Последняя совокупность решается, к примеру, способом Крамера.

Способ Гаусса

Для решения произвольных совокупностей применяют способ Гаусса. Посредством элементарных преобразований над строчками расширенную матрицу совокупности (1) приводят к виду:

Соответствующая ей совокупность, равносильная (1), примет вид:

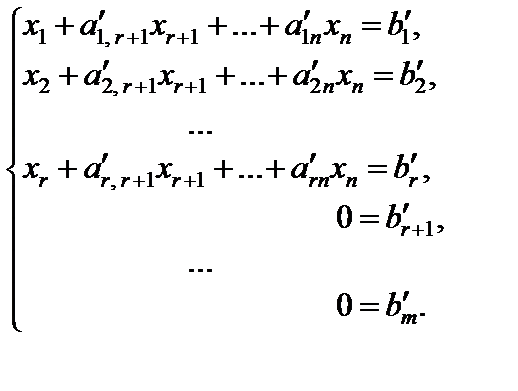(6)

В случае, если хотя бы одно из чисел br + 1, … bm превосходно от нуля, то совокупность (6), соответственно, и исходная совокупность (1) несовместны.

В случае, если br + 1 = … = bm = 0, то совокупность (6) дает возможность приобрести явное выражение для базовых малоизвестных x1, …, xr через свободные малоизвестные xr + 1, …, xn.

В случае, если r = n, то свободные малоизвестные отсутствуют, соответственно, совокупности (6) и (1) имеют единственное ответ.

На практике в большинстве случаев обходятся приведением матрицы совокупности (1) к треугольной либо трапециевидной форме, по окончании чего значения базовых переменных ищутся в обратном порядке.

37. Кривые второго порядка: окружность и эллипс (основные формулы)

Интересные записи:

• Культура как общественное явление
• Культура и проблема целостности человеческой души
• Культура первобытного человека
• Культура взаимоотношений учителя