Цель. Установить место, цели изучения понятий «первообразная», «интеграл» в курсе начал и алгебры анализа XI класса; распознать кое-какие особенности введения указанных понятий.
Оборудование. 1. Комплект кодопозитивов с условиями задач для введения понятия «первообразная», задач, каковые целесообразно применять для установления связей между понятиями «первообразная», «интеграл».
2. Схема связей между понятиями, особенностями понятий темы «Первообразная и интеграл».
Замысел реализации первой части работы
1. Установление цели, места изучения вопросов, которые связаны с понятием «интеграл».
2. Изложение содержания учебного материала темы.
3. Исполнение практических заданий, которые связаны с анализом материала темы в школьных учебных пособиях.
4. Выводы.
Главное содержание
1. Главная образовательная цель изучения темы «Первообразная и интеграл» возможно сформулирована следующим образом:
— познакомить обучающихся с операцией, которая есть обратной по отношению к операции дифференцирования функций;
— познакомить с применением способа интегрального исчисления для ответа геометрических задач, некоторых задач практического содержания.
Воспитательная и развивающая цели изучения указанной темы связаны с формированием диалектико-материалистического мировоззрения («Развитие у обучающихся верных представлений о природе математики, сущности и происхождении математических абстракций, соотношении настоящего и личного, … месте математики в роли и системе наук математического моделирования в научном познании и в практике … » [119]):
— ввести новый способ ответа последовательности задач (в частности, нахождение площади, количества фигуры), продемонстрировать известную универсальность математических способов;
— показать главные этапы ответа прикладных задач средствами математики.
Теме «Первообразная и интеграл» предшествует тема «ее применение и Производная». Такая последовательность изучения материала формирует предпосылки для
во-первых, понимания обучающимися связи между операциями интегрирования функции и дифференцирования, и главной идеи способа дифференциального и интегрального исчислений (зная функцию, возможно установить темперамент локальной ее изменяемости в зависимости от трансформации довода, и напротив: зная темперамент локальной изменяемости функции, возможно отыскать или саму функцию (при заданных начальных условиях), или семейство функций);
во-вторых, осознания обучающимися того факта, что аппарат интеграла и производной — база способа матанализа: с одной стороны, он выступает как язык, обрисовывающий многие явления, процессы мира; с другой — как инструмент, благодаря которому с учетом изюминок языка исследуются процессы и эти явления.
2. Базу содержания темы составляют два круга вопросов, любой из которых группируется около двух понятий: «первообразная», «интеграл».
В связи с понятием первообразной рассматриваются определение этого понятия, главное свойство первообразной (а также его геометрический суть), правила нахождения первообразных.
Потому, что «задача отработки навыков нахождения первообразных не ставится» (Математика в шк.- 1986.- №3.- С. 44), то упражнения, каковые обучающиеся должны мочь решать, ограничиваются несложными задачами на использование правил нахождения первообразных. Программа по математике для школы предполагает знание обучающимися первообразных степенной функции с целым ( ) показателем, функций косинус и синус.
С понятием «интеграл» связано рассмотрение вопросов о площади криволинейной трапеции, приближенном вычислении интегралов, получении формулы Ньютона-Лейбница.
В качестве примеров, иллюстрирующих использование интеграла к ответу разных задач, по большей части рассматриваются задачи на нахождение площадей криволинейных трапеций. Вопросу вычисления количеств тел посредством интеграла уделяется внимание, но данный материал делается предметом особого изучения в курсе геометрии (в учебном пособии А.В. Погорелова [113] неспециализированная формула для нахождения количеств тел вращения употребляется чтобы получить формулу, разрешающей отыскать количество его частей и шара).
Так, главное внимание при изучении темы уделяется, во-первых, нахождению первообразных и вычислению интегралов на базе таблицы первообразных и правил нахождения первообразных; во-вторых, вычислению площадей криволинейных трапеции.
3амечание. Еще раз желаем обратить внимание, что потому, что программа по математике не предусматривает формирование у обучающихся навыков интегрирования, а нацеливает только на обращение к несложным случаям применения формул для нахождения интеграла данной функции, то овладение техникой интегрирования не планируется.
3. Выделим последовательность практических заданий, на исполнение которых целесообразно ориентироваться в ходе анализа материала темы «Первообразная и интеграл» и каковые связаны с ответом на следующие вопросы:
1) Каковы задачи изучения разглядываемой темы?
Ответ на поставленный вопрос предполагает обращение к целям изучения темы «Первообразная и интеграл» в курсе математики школы и учет главного содержания данной темы. В качестве таких задач возможно указать следующие:
— ввести понятия первообразной и интеграла;
— познакомить обучающихся с фундаментальными особенностями первообразных и правилами нахождения первообразных (правилами интегрирования);
— раскрыть суть операции интегрирования как операции, обратно по отношению к операции дифференцирования заданной функции;
— выделить типы задач (нахождение площади криволинейной трапеции, нахождение количества тела, задачи с физическим содержанием); продемонстрировать, как реализуется способ интегрального исчисления. Наряду с этим обратить внимание на выделение в ходе их решения этапов, характеризующих процесс математического моделирования.
2) Какой теоретический материал нужно считать главным с учетом сформулированных выше задач и целей изучения темы «Первообразная и интеграл»?
В данный материал нужно включить:
— понятие первообразной, главное свойство первообразной;
— понятие интеграла функции;
— связь между понятиям и «интеграл» и «первообразная», которая устанавливается посредством формулы Ньютона-Лейбница;
— формула Ньютона-Лейбница как аппарат вычисления интеграла данной функции.
Каковы особенности изучения главного материала темы?
Ответ на данный вопрос предполагает раскрытие сущности разглядываемых понятий; установление связей между вводимыми элементами материала и теми, каковые уже изучены и оказывают помощь усвоению нового; обнаружение роли задач на этапах введения новых понятий, их применения, установления связей между введенными понятиям и и т.п. Наряду с этим конечно обратиться к изложению (либо разным вариантам изложения, предложив их сравнительный анализ) материала темы в имеющихся на данный момент учебных пособиях [5], [9], [13].
Предложим схемы ответов на поставленный вопрос, имея в виду вышеуказанные главные элементы материала темы.
3) Понятие первообразной, главное свойство первообразной.
Оба учебных пособия применяют следующую схему изложения материала:
а) Создание установки на изучение нового свойств и введение понятия этого понятия. С целью этого внимание обращается на две взаимно обратные задачи: ускорения тела и нахождение скорости при свободном падении (к определенному моменту времени), в случае, если известен закон трансформации пути; установление закона трансформации скорости (пути), в случае, если задан закон трансформации ускорения (скорости). Вторая задача формулируется в общем виде, то есть: дана производная некоей функции, необходимо на заданном промежутке отыскать саму функцию.
В связи с необходимостью ответа данной задачи вводим новую операцию — интегрирование.
б) С операцией интегрирования (восстановления функции по ее производной) связаны:
— понятие первообразной;
— главное свойство первообразной;
— правила нахождения первообразных.
Указанные вопросы вводятся дедуктивно, дается иллюстрация применения определения главного понятия, его особенностей посредством конкретных примеров.
Задачи, кроме применения их как средства иллюстрации вводимого в рассмотрение теоретического материала, являются средством его закрепления. Об этом свидетельствуют и формулировки задач: «доказать, что функция F есть первообразной для функции f на заданном промежутке», «Отыскать первообразную для данной функции на указанном промежутке», «Отыскать такую первообразную функции, график которой проходит через данную точку» и т.направляться.
К каким выводам приводит анализ материала учебных пособий, связанного с понятием «первообразная»?
Во-первых, преподаватель обязан подготовить изучение темы: он обязан четко воображать себе, что для этого необходимо сделать, какой материал повторить, какие конкретно приемы целесообразно применять.
Разумеется, целесообразно обратиться к
таблице производных изученных функций;
геометрическому и физическому смыслу производной;
правилам дифференцирования.
Наряду с этим возможно применять вопросы теоретического и практического содержания, намерено подобранные задачи.
Во-вторых, введение понятия первообразной и изучение фундаментального свойства первообразной полезно предварить работой с конкретными задачами.
Приведем примеры:
Задача 1. Тело движется прямолинейно со скоростью . Отыскать закон трансформации пути в зависимости от времени.
Задача 2. Отыскать уравнение кривой, угловой коэффициент касательной к которой в любой точке некоего промежутка задается следующим образом: .
В ходе ответа этих задач внимание обучающихся обращается на сообщение данного и искомого (эта функция имеется производная искомой). В первом случае скорость перемещения тела в любой момент времени известна, она есть производной соответствующего пути; значит, требуется отыскать такую функцию, производная которой равна 2t. Во втором случае дана формула, определяющая производную некоей функции в каждой точке фиксированного промежутка, а необходимо отыскать функцию (производная функция равна );
Какие конкретно выводы необходимо осуществить в следствии анализа ответов обеих задач?
— Ответ пребывало в нахождении функции по известной производной.
— Функций, каковые удовлетворяют условиям предложенных задач, вечно довольно много.
Так, мы, с одной стороны, создали базу для введения понятия первообразной и операции интегрирования как обратной операции дифференцирования функции, а с другой, оказываемся в условиях доказательства теоремы и целесообразности формулирования, которая высказывает главное свойство первообразной.
В-третьих, целесообразно обратить внимание обучающихся на следующее: запись F(х)+C (неспециализированный вид первообразных для функции f(х) на заданном промежутке) связывает нас, с одной стороны, с произвольным значением постоянной С, а с другой, в зависимости от условия предложенной для ответа задачи — с конкретным. С целью этого возможно возвратиться к анализу ответов уже рассмотренных задач.
В первой из них в качестве искомой могла быть указана , к примеру, функция вида ,во второй — (С — некая постоянная). Дабы продемонстрировать, что учет конкретных условий задачи влечет обращение к в полной мере определенной первообразной, возможно предложить обучающимся отыскать уравнение пути, в случае, если за 2 с тело прошло 15 м (отыскать уравнение кривой, проходящей через фиксированную точку А (1; 2)). Ответ обеих задач связано с нахождением тех первообразных заданных функций, каковые удовлетворяют указанным начальным условиям. Любая из таких первообразных определяется конкретно:
Работа с задачами убеждает получающих образование том, что их ответ связано с выделением из множества первообразных данной функции в полной мере определенных конкретных первообразных (конкретно с этим мы сталкиваемся при ответе задач практического содержания).
Увидим, что обращение к указанным задачам позволяет создать базу для раскрытия геометрического смысла фундаментального свойства первообразной.
В-четвертых, изучение вопроса о правилах отыскания первообразных конечно связать с обращением к двум взаимнообратным операциям: интегрированию и дифференцированию.
К примеру, введение третьего правила (в случае, если F (х) — первообразная для функции f (х), а и b — постоянные, то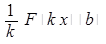 
имеется первообразная для функции ),возможно предварить рассмотрением с обучающимися следующих задач:
— отыскать производные функций
— отыскать хотя бы одну первообразную для функции
Анализ ответов этих задач и ведет к формулировке указанного правила нахождения первообразных, подтверждение которого возможно предложить обучающимся совершить самостоятельно.
4. Введение понятия интеграла. Установление связи между понятиями «интеграл» и «первообразная».
направляться обратиться к схемам изложения материала, связанного с указанным вопросом, в учебном пособии [9] и пробном книжке [5], и установить, в чем их отличие.
Учебное пособие [9] разглядывает:
1) Площадь криволинейной трапеции как приращение первообразной постоянной функции, заданной на отрезке:
— понятие криволинейной трапеции;
— теорема, дающая один из подходов к задаче нахождения площади криволинейной трапеции ( где F — первообразная для постоянной, неотрицательной на отрезке [a; b] функции f);
— утверждение: каждая постоянная на данном промежутке функция имеет на нем первообразную.
2) Интеграл:
— второй подход к задаче нахождения площади криволинейной трапеции (практически рассмотрение предела интегральных сумм);
— понятие интеграла как числа, к которому стремятся интегральные суммы (при );
— связь между интегралом постоянной, неотрицательной на отрезке [a; b]функции и площадью соответствующей криволинейной трапеции.
3) Формулу Ньютона-Лейбница:
— сравнение результатов ответа задачи о площади криволинейной трапеции при двух рассмотренных подходах (вывод: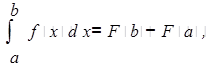 
где F — первообразная для постоянной, неотрицательной на отрезке [a; b]функции f);
— вывод о справедливости взятой формулы для любой постоянной на отрезке функции (без доказательства).
Изложение соответствующего материала в пробном книжке [5] принципиально не отличается от изложения в пособии [9], не смотря на то, что имеется расхождения в последовательности рассмотрения отдельных вопросов. Схема изложения возможно условно представлена следующим образом: понятие криволинейной трапеции — площадь криволинейной трапеции как предел соответствующих интегральных сумм (площадь под графиком некоей функции, заданной на отрезке) — интеграл от функции на отрезке как предел интегральных сумм — связь между интегралом постоянной неотрицательной на отрезке функции и площадью криволинейной трапеции — получение формулы Ньютона-Лейбница, устанавливающей связь между интегралом и первообразной и разрешающей вычислить интеграл (равно как и в пособии [9], формула Ньютона-Лейбница выводится на базе наглядных представлений в ходе ответа задачи на нахождение площади криволинейной трапеции как приращения первообразной).
С разглядываемым теоретическим материалом связаны два главных вида задач. Они, в большинстве случаев, предлагаются в следующих формулировках: вычислить площадь фигуры, ограниченной линиями; вычислить интеграл.
Замечание. К понятию интеграла, как мы знаем, приводит не только задача о площади криволинейной трапеции, но и другие задачи, к примеру задача о работе силы, задача о количестве электричества, протекающем за этот временной отрезок через поперечное сечение проводника. С методикой применения этих задач для введения понятия «интеграл» возможно познакомиться в книге [70].
Анализ материала учебных пособий, связанного с введением понятия «интеграл» и получением метода вычисления интегралов, ведет к последовательности ответственных в методическом отношении выводов, каковые полезно иметь в виду, разрабатывая методику изучения отдельных вопросов разглядываемой темы. Что это за выводы?
Во-первых, формула Ньютона и определение интеграла-Лейбница позволяют доказать последовательность довольно часто используемых особенностей интеграла. Ясно, что в ходе их доказательства понятие интеграла, его геометрический суть будут глубже усваиваться обучающимися. Возможно предложить, к примеру, установить справедливость следующих утверждений:
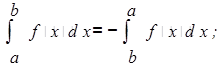
— в случае, если функция f имеет на отрезке [a; b]первообразную, то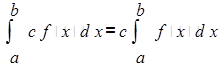 
(с — некая постоянная);
— в случае, если функции и имеют на отрезке [a; b]первообразные, то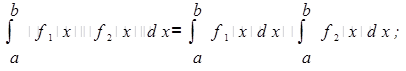 
— в случае, если то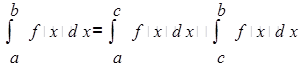 
(№ 455, [9]);
— доказать формулу вычисления производной от интеграла с переменным верхним пределом интегрирования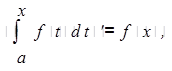 
где f(х) — функция, постоянная на промежутке, содержащем точки а и х (№457, [9]).
Предложенные упражнения нужны еще и по причине того, что в ходе их ответы устанавливаются (и употребляются) связи между операциями интегрирования и дифференцирования, между понятиями «производная», «первообразная», «интеграл» и их особенностями.
направляться поразмыслить о месте включения этих упражнений в учебный материал и методике работы с ними.
Во-вторых, понятие интеграла вводится для функции, постоянной на некоем отрезке (такая функция имеет на этом отрезке первообразную). Сознательному усвоению обучающимися этого понятия (и понятия первообразной) будет содействовать особое привлечение внимания школьников к этому факту. С целью этого смогут быть использованы задачи, к примеру, такие:
Задача 1. Допустимо ли вычислить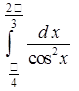 
(подынтегральная функция имеет точку разрыва 
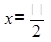, принадлежащую отрезку 
)?
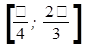Задача 2. Отыскать неточность в вычислении интеграла
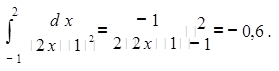
(О том, что неточность вправду допущена, свидетельствует итог: интеграл от хорошей функции был отрицательным числом.)
Задача 3. При каких значениях пределов интегрирования интеграл существует
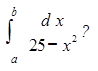
(В точках подынтегральная функция терпит разрыв; исходя из этого возможно сказать о следующих условиях, которым должны удовлетворять значения пределов интегрирования:
- и ;
- ;
- .)
Задача 4. Вычислить:
а)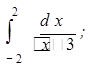 
б) 
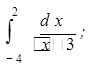в)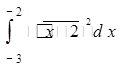 
.
(В двух последних случаях интегралы не смогут быть вычислены, поскольку подынтегральная функция не выяснена в каждой точке отрезка, заданного пределами интегрирования.)
В-третьих, установление связей между понятиям и «интеграл» и «первообразная» (правильнее приращение первообразной) происходит через обращение к площади соответствующей криволинейной трапеции. Следовательно, большое внимание при изучении материала необходимо выделить геометрическому смыслу интеграла, не ограничиваясь наряду с этим лишь применением геометрических иллюстраций в ходе ответа задач на вычисление интегралов.
Целесообразно намерено выделить, что, опираясь на геометрический суть интеграла, время от времени приобретаем возможность
установить существование более несложного если сравнивать с рассмотренным метода вычисления интегралов (к примеру, по симметричному относительно точки О промежутку от четной либо нечетной функции). Сделать это возможно, обратившись к задачам:
Задача 1. Продемонстрировать, что в случае, если f — постоянная, четная на отрезке [-а; а]функция, то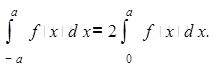 
Задача 2. Продемонстрировать, что в случае, если f — постоянная, нечетная на отрезке [-а; а]функция, то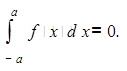 
Задача 3. Вычислить:
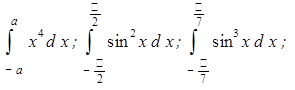
не только вычислять площади фигур, но и обнаружить числовые значения интеграла, вычисление которых по известным обучающимся формулам выполнить не удается.
К примеру:
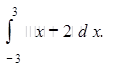
Замечание. Возможно предложить следующую схему введения понятия «интеграл»:
понятие криволинейной трапеции — площадь криволинейной трапеции как приращение первообразной соответствующей постоянной функции, заданной на отрезке, — понятие интеграла (интеграл постоянной функции на отрезке имеется приращение первообразной для данной функции:
).
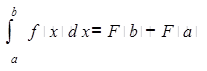В чем преимущества и недочёты предложенной схемы введения понятия «интеграл»? Допустимо ли направляться ей при изучении материала соответствующей темы школьного курса математики? Как должно быть организовано в этом случае изучение материала?
5. Какова схема, отражающая связи между понятиям и, особенностями понятий темы «Первообразная и интеграл»?
Эту схему наглядно возможно представить, к примеру, следующим образом:
 |
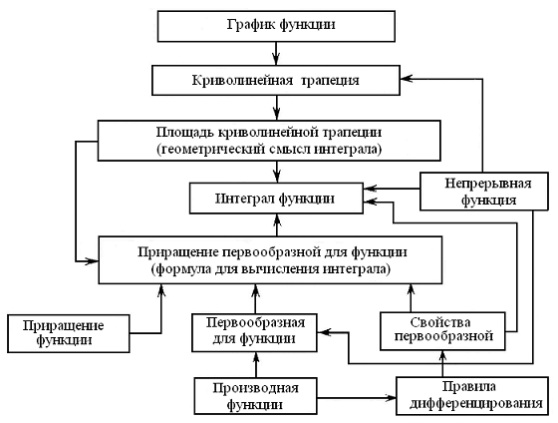Анализ предложенной схемы убеждает в правомерности методических выводов, каковые сделаны на базе обращения к материалу учебных пособий [5], [9], [13] и отражены в этом параграфе.
6. Обратимся к задачам, каковые предложены учебными пособиям и [5] и [9] в теме «Первообразная и интеграл».
Возможно ли утверждать, что, разглядывая с обучающимися методы ответа этих задач, организуя независимую работу школьников с ними, мы реализуем главные цели изучения темы?
Ответ на данный вопрос предполагает выделение трех групп задач:
— задачи, каковые конкретно направлены на формирование понятий, применение особенностей понятий, закрепление способов деятельности с введенными понятиям и (задачи, каковые в большей мере несут дидактическую функцию);
— задачи, в следствии ответа которых приобретаем или новый факт (он бывает нужен в будущем), или новый метод ответа задач определенного вида (познавательные задачи);
— задачи, в ходе ответа которых формируются операции, приемы мышления, создаются предпосылки для осуществления творческой деятельности, среди них и математической (задачи, главная функция которых развивающая).
Разумеется, что с группой общеобразовательных целей изучения темы в большей мере обязана соотноситься несколько задач с дидактическими функциями, последовательность познавательных задач при определенных условиях также возможно использован для реализации указанных целей.
Воспитательная и развивающая цели изучения материала достигаются в ходе ответа всех трех групп задач, но громаднейшую значимость в этом случае имеют развивающие и познавательные задачи.
Ориентируясь на материал пособий [5], [9], направляться отнести предлагаемые задачи к одной из вышеуказанных групп и указать, какова конкретная «нагрузка» отдельных задач либо их серий.
7. умениями и Какими знаниями должны обладать обучающиеся к моменту изучения темы «Первообразная и интеграл», какие конкретно знания, умения формируются в ходе изучения темы?
Ответ на указанный вопрос обязан определяться программой по математике для школы , целями изучения темы, и необходимыми результатами, каковые должны быть достигнуты всеми без исключения учащимися в следствии работы с учебным материалом (необходимые результаты обучения обучающихся по теме «Первообразная и интеграл» приведены в издании «Математика в школе».- 1985.- №4.- С. 28).
8. Выводы:
— понятие интеграла в курсе математики школы вводится на базе понятия предела соответствующих интегральных сумм;
— вычисление интегралов связано с применением приращения соответствующих первообразных (формула Ньютона-Лейбница);
— площадь криволинейной трапеции есть главным звеном, благодаря которому устанавливается связь между приращением интеграла и понятием функции соответствующей первообразной. Установление данной связи приводит и к методу (одному из вероятных) вычисления интеграла;
— громадное внимание в ходе изучения материала темы необходимо выделить работе, которая связана с разъяснением обучающимся геометрического смысла интеграла и показом возможностей его применения для ответа последовательности конкретных задач.
Задания для независимой работы
1. Ориентируясь на методические указания, приведенные в настоящих материалах, создайте методику введения понятия «первообразная» и фундаментального свойства первообразной.
Литература: [5], [9], [13], [70], [38].
2. Продумайте методику применения задач при введении понятия «интеграл» и установлении его особенностей, связей с понятием «первообразная».
Литература: [61], [70], [74], [38].
3. Проанализируйте материалы контрольной работы по теме «Первообразная и интеграл» (см.: Математика в шк.- 1986.-4.- С. 20; контрольная работа № 3) и соотнесите предложенные задания с заданиями соответствующего раздела «Необходимые результаты обучения» (см.: Математика в шк.- 1985.- № 4.- С. 28).
4. Познакомьтесь с примерным поурочным планированием материала темы «Первообразная и интеграл» (см.: Математика в шк.- 1986.- № 3.- С. 47).
II. Поурочное планирование изучения материала темы «Первообразная и интеграл»
Цель. Установить круг задач, в ходе ответа которых применяются способ вычисления и понятие интеграла интеграла конкретной функции; с учетом задач и целей темы, и конкретного содержания книжки выполнить поурочное разбиение учебного материала.
Замысел реализации второй части работы
1. Виды задач, для ответа которых употребляется способ интегрального исчисления.
2. Составление подробного замысла изучения материала темы «Первообразная и интеграл».
Главное содержание
1. Программа по математике не ставит цели научитьшкольников использовать способ интегрального исчисления при ответе задач; предполагается только знакомство с применением способа, иллюстрация применения интеграла к ответу задач.
Какие конкретно виды задач, в базе ответа которых лежит способ интегрального исчисления, возможно выделить? Какие конкретно из этих видов рассматриваются в ходе изучения темы?
для ответа на поставленные вопросы целесообразно обратиться к следующей литературе: [5], [9], [1], [13], [22], [64], [68], [70], [83].
Главный вид задач, при ответе которых мы имеем возможность реализовать цели изучения темы, и особенно воспитательную и развивающую,- это задачи на нахождение площадей плоских фигур.
направляться продумать:
— как именно реализуются в этом случае главные этапы ответа прикладных задач средствами математики;
— как, имея в виду разглядываемый вид задач, продемонстрировать обучающимся универсальность математических способов.
2. Составляя тематический замысел изучения вопросов, которые связаны с понятиями «первообразная», «интеграл», необходимо особенное внимание выделить:
— формулированию цели, конкретных задач каждого урока;
— обоснованию отбора учебного материала на урок (как теоретического, так и комплекта задач);
— четкому указанию тех конкретных связей, каковые должны установиться между элементами нового и уже изученного материала (внутрипредметные связи), между элементами материала данного других предметов и предмета, к примеру физики (межпредметные связи).
Задание для независимой работы
Закончите составление замысла изучения со школьниками материала темы «Первообразная и интеграл».
Литература: [5], [9], [13], [22], [64], [61], [68], [70], [74], [83], [96], [125].