«Одной из наиболее значимых схем, по которой идет применение результатов теории возможностей в технике и естествознании, пребывает в следующем. Уверены в том, что процесс протекает под влиянием солидного числа независимо действующих случайных факторов, любой из которых только ничтожно мало изменяет течение явления либо процесса. Исследователь, интересующийся изучением процесса в целом , а не действием отдельных факторов, замечает только суммарное воздействие этих факторов.
Таки образом, появляется задача изучения закономерностей, характерным суммам солидного числа свободных случайных размеров, любая из которых оказывает только малое действие на сумму»
(Б.В.Гнеденко «Курс теории возможностей)
Замечание 22.4. Обычным и самым «насущным» примером для того чтобы рода сумм есть «суммарная неточность» — неточности, вызванные состоянием измерительной техники, «антропогенный фактор» — неточности наблюдателя и пр.
Любой из этих факторов порождает только весьма малого неточность. Но все они совместно, «в сумме», способны сказаться на итогах измерений очень ощутимо. «В противном случае говоря, практически замечаемая неточность измерения будет случайной величиной, являющейся суммой огромного числа ничтожных по величине и свободных между собой случайных размеров. И не смотря на то, что эти последние малоизвестны, кроме этого как малоизвестны и их функции распределения, их влияние на результаты измерений заметно, и исходя из этого должно быть подвергнуто изучению»
(В том месте же)
Все формы центральной предельной теоремы посвящены установлению условий, при которых появляется обычный закон распределения, поскольку эти условия на практике часто выполняются, формальный закон есть самым распространенным из законов распределения, чаще всего видящимся в случайных явлениях природы. Он появляется в любых ситуациях, в то время, когда исследуемая случайная величина возможно представлена в виде суммы большого числа свободных (либо слабо зависимых) элементарных слагаемых, каждое из которых в отдельности относительно мало воздействует на сумму.
В качестве иллюстрации центральной предельной теоремы довольно часто разглядывают стрельбу (из лука, пушки и пр.) – исторически одну из первых моделей для изучения суммарных погрешностей. В случае, если стрельба ведется по плоской мишени, то точка попадания определяется двумя размерами – отклонением по вертикали и по горизонтали от центра мишени (где надеется начало координат). Разглядим одно из них, к примеру, по вертикали. Оно позвано совокупным действием солидного числа факторов (погода, незначительные недостатки боеприпаса, неточности престреливания, определения цели и пр.), любой из которых относительно мелок. Любая из этих обстоятельств формирует элементарную неточность — отклонение боеприпаса от цели, и координата боеприпаса Y возможно представлена как сумма таких элементарных отклонений: Y = Y1 + Y2 + Y 3+ …Yn+…, где Y1 , Y2 , Y 3, Yn — отклонения, вызванные отдельными факторами. Этих факторов довольно много, между собой они являются по большей части свободными, по влиянию на сумму отдельные слагаемые можно считать малыми, то в соответствии с центральной предельной теореме, величина Y обязана подчиняться закону распределения, близкому к обычному.
Обычный закон распределения есть главным во многих областях, первым делом в теории неточностей измерения, первым делом в астрономии и физике. (Еще в середине 19 века Ф.Бессель насчитал 11 типов неточностей, каковые может совершить одинаковый астролог, замечающий за одними и теми же объектами одними и теми же устройствами). Конкретно для обоснования данной теории обычный закон и был в первый раз обоснован Гауссом и Лапласом. Как правило неточности, появляющиеся при измерении тex либо иных физических размеров, распределяются конкретно по обычному закону; обстоятельство этого в том, что такие неточности, в большинстве случаев, складываются из бессчётных свободных элементарных неточностей, порождаемых разными обстоятельствами.
Замечание 22.5. В действительности история с изучением суммарных неточностей измерений более сложная. В ее развитие внесли вклад многие ученые, а также Д.Бернулли (изучение погрешности при стрельбе из лука), а А.де Муавр в первый раз взял колоколообразную кривую (кривую Гаусса), аппроксимируя числа треугольника Паскаля на строчках с тысячными номерами)
Замечание 22.6. Классическим для математики образом в соответствующей теории рассматривается не сумма большого (но конечного) числа слагаемых, а последовательность сумм со все возрастающим (вечно) числом слагаемых.
Sn = Х1 + Х2 +… + Хn , n ? 1
ЕХi = a
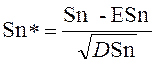
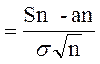
Тогда Sn* пытается по распределению к случайной величине Z, имеющей стандартное обычное распределение с соответствующей функцией распределения 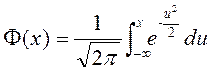
Замечание 22.7. Суммы Sn* именуются время от времени нормированными (либо стандартизированными) суммами
Замечание 22.8. Центральная предельная теорема есть обобщением теоремы Муавра-Лапласа
Замечании 22.9. Центральной предельной теоремой в большинстве случаев именуют утверждение о сходимости, в котором в качестве предела появляется обычное распределение. Исторически такие неточности появились как неточности наблюдений, подверженных влиянию случайности. Исходя из этого теорему возможно осознавать как безграничное утверждение о том, что при «обычных» условиях на слагаемые стандартизованная сумма распределена в соответствии с обычному закону, именуемому кроме этого «функцией неточностей».
Пример 22.2.
Случайная величина Х есть средним арифметическим из 3200 случайных размеров с дисперсией и 3 математическим ожиданием 2. Посредством центральной предельной теоремы оценить возможность попадания Х в промежуток (2,9 , 3,1)
Потому, что Х=Sn /n = (Х1 + Х2 +… + Хn )/n,
Sn* = (Х – 3)?40 имеет стандартное вероятность попадания и нормальное распределение значения Х в промежуток (2,9 , 3,1) будет равняется P{2,9 X 3,1} = P{(2,9 – 3)?40 Sn* (3,1 – 3)?40}, каковая имеется разность значений функции распределения стандартного обычного закона в точках (4) и (-4), другими словами Ф(4) – Ф(-4) , что, в силу нечетности функции Ф, будет равняться 2?Ф(4) = 2?0,49997=0,99994 (значение функции Лапласа берется из таблицы).